Коскова Т. А.
Учитель математики высшей категории
ГБОУ Лицей 533 г. Санкт-Петербурга
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка. Урок-презентация по геометрии по теме Призма для 10 класса
Содержание
- 1. Методическая разработка. Урок-презентация по геометрии по теме Призма для 10 класса
- 2. «Призма»
- 3. Слайд 3
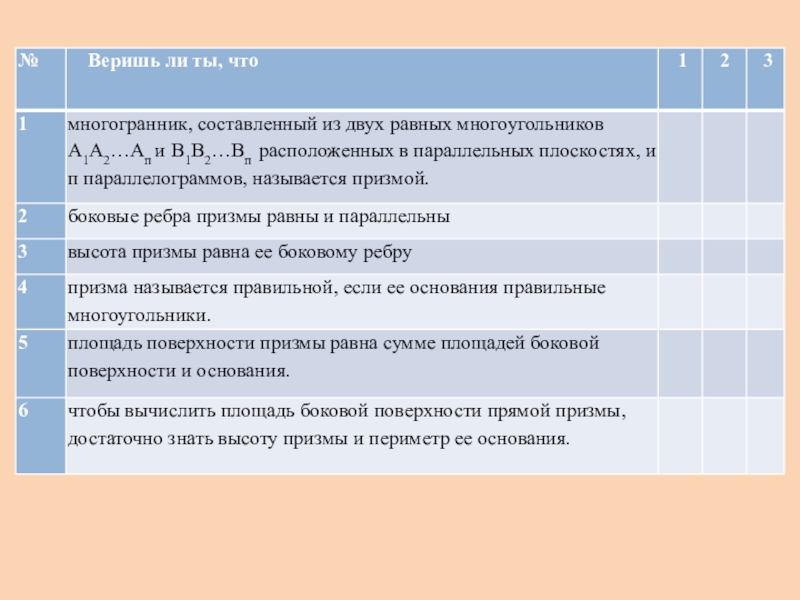
- 4. Веришь ли ты, что многогранник, составленный из
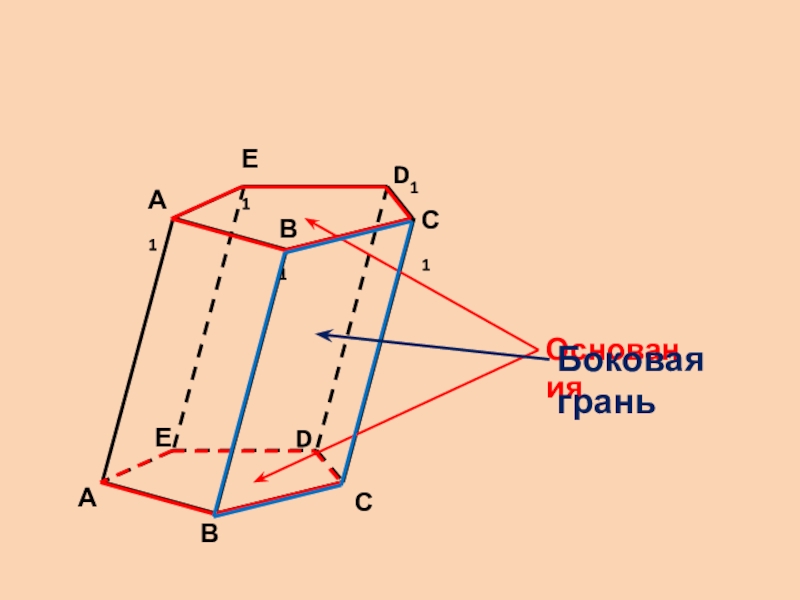
- 5. АВСС1DЕА1В1D1 Е1ОснованияБоковая грань
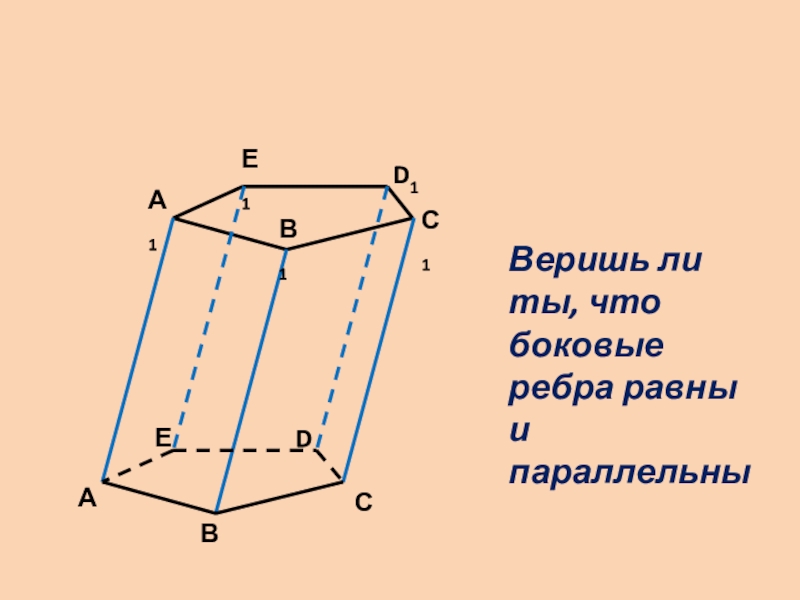
- 6. АВСС1DЕА1В1D1 Е1Веришь ли ты, что боковые ребра равны и параллельны
- 7. Веришь ли, чтовысота призмы равна ее боковому ребру
- 8. АВСС1DА1В1D1 Е1Наклонная призмаHЕПрямая призмаВысота
- 9. ПризмаНаклоннаяПрямая( Боковое ребро перпендикулярно основанию)( Боковое ребро
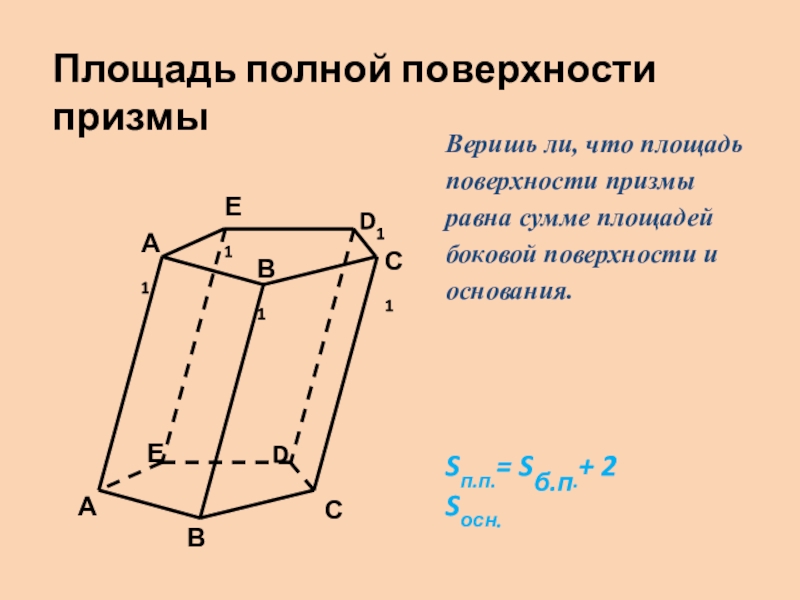
- 10. АВСС1DЕА1В1D1 Е1Площадь полной поверхности призмыSп.п.= Sб.п.+ 2
- 11. Веришь ли ты, чтобы вычислить площадь боковой
- 12. ЕАВСDА1Е1D1 С1В1Площадь боковой поверхности прямой призмыSб.п.= h
- 13. Параллелепипед (частный случай призмы)Прямой
- 14. Знал. Узнал новое. Не понял.
- 15. Спасибо за внимание
«Призма»
Слайд 1Из опыта работы в
технологии развития
критического мышления.
Урок по теме «Призма»
10 класс
Слайд 4Веришь ли ты, что многогранник, составленный из двух равных многоугольников А1А2…Ап
и В1В2…Вп расположенных в параллельных плоскостях, и п параллелограммов, называется призмой.
Слайд 9Призма
Наклонная
Прямая
( Боковое ребро перпендикулярно основанию)
( Боковое ребро перпендикулярно основанию.
Основания – правильные
многоугольники)
Правильная
Веришь ли ты, что призма называется правильной, если ее основания правильные многоугольники
Слайд 10А
В
С
С1
D
Е
А1
В1
D1
Е1
Площадь полной поверхности призмы
Sп.п.= Sб.п.+ 2 Sосн.
Веришь ли, что площадь
поверхности призмы равна сумме площадей боковой поверхности и основания.
Слайд 11Веришь ли ты, чтобы вычислить площадь боковой поверхности прямой призмы, достаточно
знать высоту призмы и периметр ее основания.
Слайд 12Е
А
В
С
D
А1
Е1
D1
С1
В1
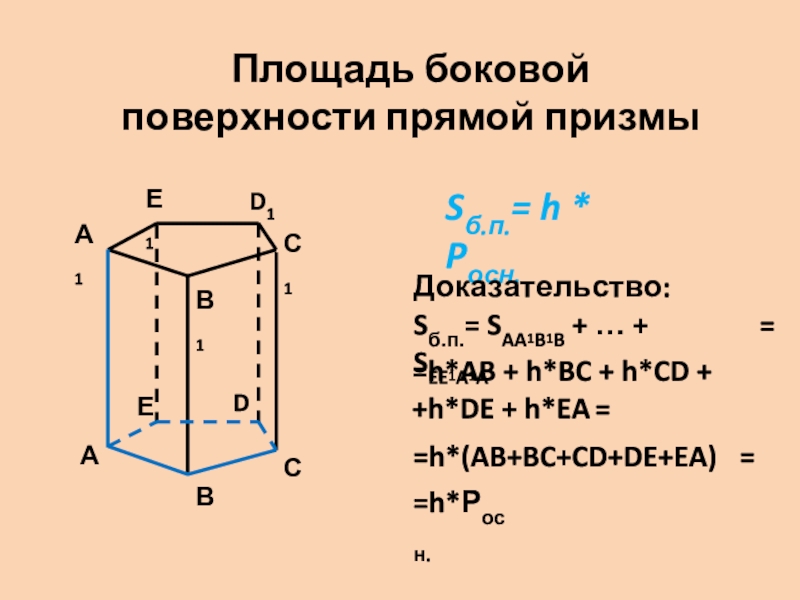
Площадь боковой поверхности прямой призмы
Sб.п.= h * Pосн.
Доказательство:
Sб.п.= SAA1B1B +
… + SEE1A1A
=h*AB + h*BC + h*CD + +h*DE + h*EA
=
=h*(AB+BC+CD+DE+EA)
=h*Росн.
=
=
Слайд 13Параллелепипед
(частный случай призмы)
Прямой
(боковое ребро перпендикулярно плоскости основания)
Прямоугольный
( - прямой параллелепипед;
- основание – прямоугольник )
Наклонный
(боковое ребро не перпендикулярно плоскости основания)
Куб