Презентация, доклад на тему Геометрические задачи в ОГЭ

Содержание

1. Геометрические задачи в ОГЭ
2. Доказательство: OE – Медиана треугольника COD.Так как
3. Решение: Пусть LC — биссектриса угла KLM
4. Аналогично, пусть MD — биссектриса угла LMN.
5. По условию окружность проходит через точку В
6. ∠MBO =∠BAC – это накрест лежащие углы
7. Пусть в треугольнике АВС проведена медиана ВМ
8. Пусть общая вершина квадратов – точка О.
9. Пусть в треугольнике ABC отрезок BM служит
10. В равнобедренной трапеции ABCD с основаниями AD
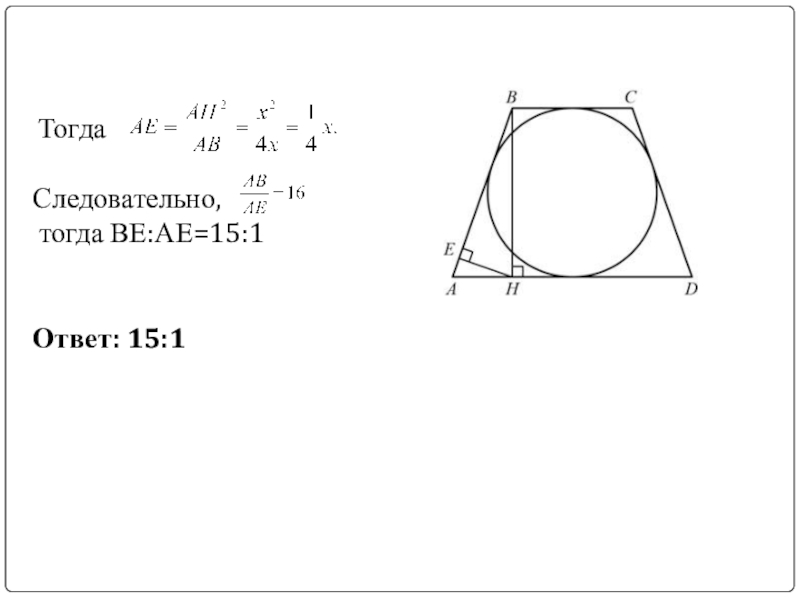
11. ТогдаСледовательно, тогда ВЕ:АЕ=15:1Ответ: 15:1

Доказательство: OE – Медиана треугольника COD.Так как OC = OD, треугольник COD равнобедренный. Следовательно, OE является высотой треугольника COD. Поэтому AB ⊥ CDДокажите, что диаметр окружности, проведенный через середину хорды(не являющейся диаметром), перпендикулярен этой хорде

Главная
Геометрия
Геометрические задачи в ОГЭ

Слайд 1Презентацию подготовила: Н.С. Лапина
Геометрические задачи в ОГЭ

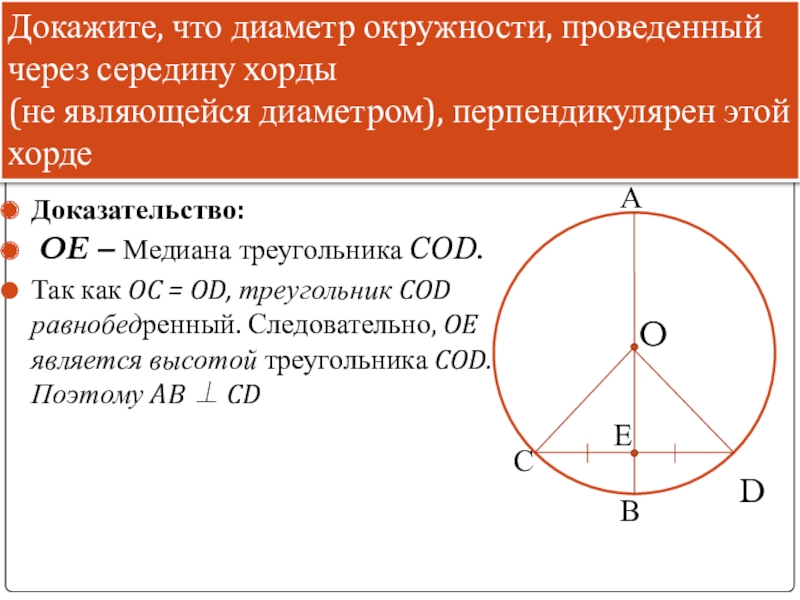
Слайд 2Доказательство:
OE – Медиана треугольника COD.
Так как OC = OD, треугольник

COD равнобедренный. Следовательно, OE является высотой треугольника COD. Поэтому AB ⊥ CD

Докажите, что диаметр окружности, проведенный через середину хорды
(не являющейся диаметром), перпендикулярен этой хорде

Доказательство: OE – Медиана треугольника COD.Так как OC = OD, треугольник COD равнобедренный. Следовательно, OE является высотой

Слайд 3
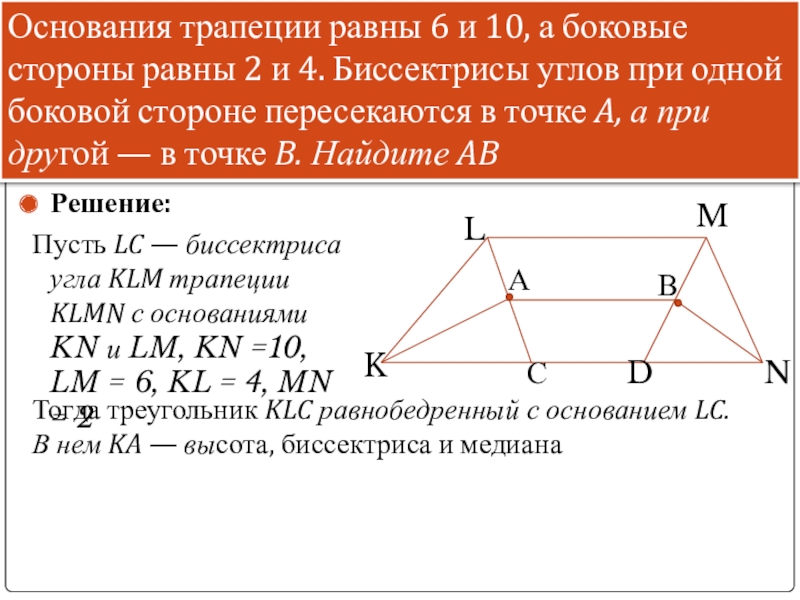
Решение:
Пусть LC — биссектриса угла KLM трапеции KLMN с основаниями

KN и LM, KN =10, LM = 6, KL = 4, MN = 2

Основания трапеции равны 6 и 10, а боковые стороны равны 2 и 4. Биссектрисы углов при одной боковой стороне пересекаются в точке A, а при другой — в точке B. Найдите AB

Тогда треугольник KLC равнобедренный с основанием LC. В нем KA — высота, биссектриса и медиана

Решение: Пусть LC — биссектриса угла KLM трапеции KLMN с основаниями KN и LM, KN =10, LM

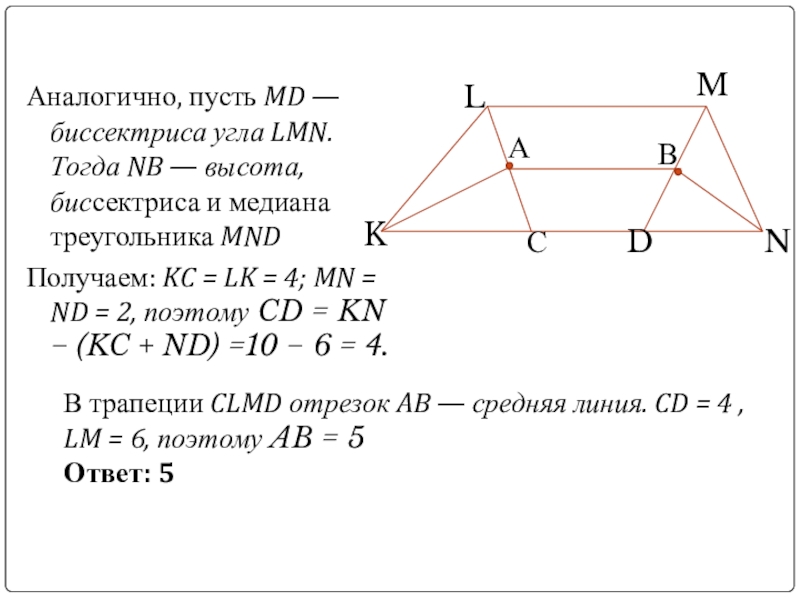
Слайд 4Аналогично, пусть MD — биссектриса угла LMN. Тогда NB — высота,

биссектриса и медиана треугольника MND
Получаем: KC = LK = 4; MN = ND = 2, поэтому CD = KN − (KC + ND) =10 − 6 = 4.

В трапеции CLMD отрезок AB — средняя линия. CD = 4 , LM = 6, поэтому AB = 5
Ответ: 5

Аналогично, пусть MD — биссектриса угла LMN. Тогда NB — высота, биссектриса и медиана треугольника MND Получаем:

Слайд 5
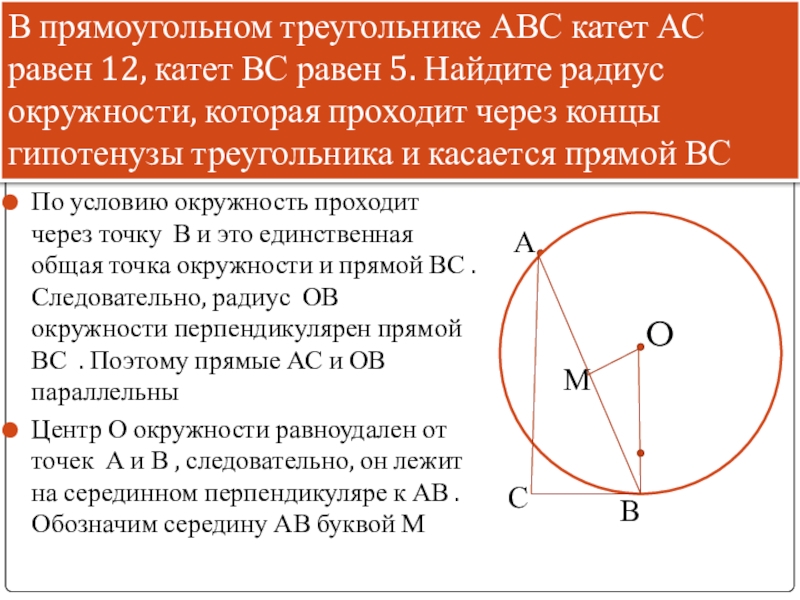
По условию окружность проходит через точку В и это единственная общая

точка окружности и прямой ВС . Следовательно, радиус ОВ окружности перпендикулярен прямой ВС . Поэтому прямые АС и ОВ параллельны
Центр О окружности равноудален от точек А и В , следовательно, он лежит на серединном перпендикуляре к АВ . Обозначим середину АВ буквой М

В прямоугольном треугольнике АВС катет АС равен 12, катет ВС равен 5. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой ВС

По условию окружность проходит через точку В и это единственная общая точка окружности и прямой ВС .

Слайд 6∠MBO =∠BAC – это накрест лежащие углы при параллельных прямых и

секущей АВ .
Следовательно, прямоугольные треугольники АСВ и ВМО подобны.

Тогда

Ответ:

∠MBO =∠BAC – это накрест лежащие углы при параллельных прямых и секущей АВ .Следовательно, прямоугольные треугольники АСВ

Слайд 7
Пусть в треугольнике АВС проведена медиана ВМ , которая равна половине

стороны АС . Значит, треугольники АВМ и СВМ равнобедренные
Пусть ∠ВАМ=∠АВМ=α, ∠ВСМ=∠СВМ=β. Тогда 2α+2β=180˚, откуда ∠АВС=∠АВМ+ ∠СВМ =α+β=90˚
Ответ: 90˚

Медиана треугольника равна половине стороны, к которой она проведена. Докажите, что данный треугольник прямоугольный

Пусть в треугольнике АВС проведена медиана ВМ , которая равна половине стороны АС . Значит, треугольники АВМ

Слайд 8
Пусть общая вершина квадратов – точка О. АО ⏊ОС и ВО

⏊ОЕ.
Следовательно, ∠АОВ=∠СОЕ. Тогда треугольники АОВ и СОЕ равны по двум сторонам и углу между ними. Следовательно, АВ=СЕ как соответствующие стороны равных треугольников

Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки АВ и СЕ равны

Пусть общая вершина квадратов – точка О. АО ⏊ОС и ВО ⏊ОЕ.Следовательно, ∠АОВ=∠СОЕ. Тогда треугольники АОВ и

Слайд 9
Пусть в треугольнике ABC отрезок BM служит медианой, при этом ∠

ABM= 90°, ∠CBM=30°. Возьмем на продолжении отрезка BM точку D так, что BM = MD.

Ответ: 1/2

.

Тогда треугольники ABM и CDM равны по двум сторонам и углу между ними. Значит, ∠BDC=90°. Поэтому
треугольник BDC - прямоугольный с углом CBD , равным 30°. Следовательно,

Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30˚ и 90˚

Пусть в треугольнике ABC отрезок BM служит медианой, при этом ∠ ABM= 90°, ∠CBM=30°. Возьмем на продолжении

Слайд 10
В равнобедренной трапеции ABCD с основаниями AD и BC, описанной около

некоторой окружности, проведена высота BH. Из точки H опущен перпендикуляр HE на прямую AB. В каком отношении точка E делит отрезок AB, если известно, что BC:AD=3:5?

Пусть BC=3x, AD=5x . Суммы противоположных сторон у описанного около
окружности четырехугольника равны, поэтому AB+CD=8x и, значит, AB=4x

Применим соотношение в прямоугольном треугольнике: AH2=AE⋅AB