- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Формирование познавательных универсальных учебных действий при обучении геометрии в основной школе
Содержание
- 1. Формирование познавательных универсальных учебных действий при обучении геометрии в основной школе
- 2. Цель исследования: разработать способы формирования познавательных универсальных
- 3. Задачи:1. Выявить роль системно-деятельностного подхода в обучении.2. Охарактеризовать сущность
- 4. Глава 1. Теоретические основы формирования познавательных универсальных учебных действий в процессе обучения
- 5. - развитие детей, формирование активных личностей и компетентных профессионалов. Значение системно-деятельностного подхода в современном образовании
- 6. Универсальные учебные действия – это умение учиться, т.е. способность к саморазвитию и самосовершенствованию.
- 7. Слайд 7
- 8. - сравнение; -
- 9. - составление схемы определения понятия; -
- 10. Глава 2. Методические особенности формирования познавательных универсальных учебных действий при обучении геометрии в основной школе
- 11. «Вертикальные и смежные углы»Формируемые познавательные УУД: раскрытие
- 12. 1. Раскройте термины понятий «Угол», «Биссектриса
- 13. «Свойства смежных и вертикальных углов»Формируемые познавательные УУД:
- 14. «Равнобедренный треугольник»Формируемые познавательные УУД: пошаговая запись решения,
- 15. «Равнобедренный треугольник»Формируемые познавательные УУД: пошаговая запись решения,
- 16. Задача . По данным рисунка 25 найдите
- 17. Задача . По данным рисунка 25 найдите
- 18. Задача . Используя данные рисунка 34 докажите,
- 19. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Формирование познавательных универсальных учебных действий при обучении геометрии в основной школе
Слайд 2
Цель исследования: разработать способы формирования познавательных универсальных учебных действий при обучении
Объект исследования: процесс обучения геометрии в основной школе.
Предмет исследования: процесс формирования познавательных универсальных учебных действий при обучении геометрии в основной школе.
Слайд 3
Задачи:
1. Выявить роль системно-деятельностного подхода в обучении.
2. Охарактеризовать сущность понятий «универсальные учебные действия»,
3. Разработать комплекс заданий, направленные на формирование познавательных универсальных учебных действий при введении математических понятий.
4. Разработать задания, способствующие формированию познавательных универсальных учебных действий при обучении доказательству теорем и решению задач курса геометрии основной школы.
Слайд 4Глава 1. Теоретические основы формирования познавательных универсальных учебных действий в процессе
Слайд 5- развитие детей, формирование активных личностей и компетентных профессионалов.
Значение системно-деятельностного подхода
Слайд 6
Универсальные учебные действия – это умение учиться, т.е. способность к
Слайд 8 - сравнение; - раскрытие термина понятия; - подведение под понятие; - анализ формулировки теоремы; -
Логические УУД
Слайд 9 - составление схемы определения понятия; - составление схемы поиска решения задачи; - составление
Общеучебные УУД
Слайд 10Глава 2. Методические особенности формирования познавательных универсальных учебных действий при обучении
в основной школе
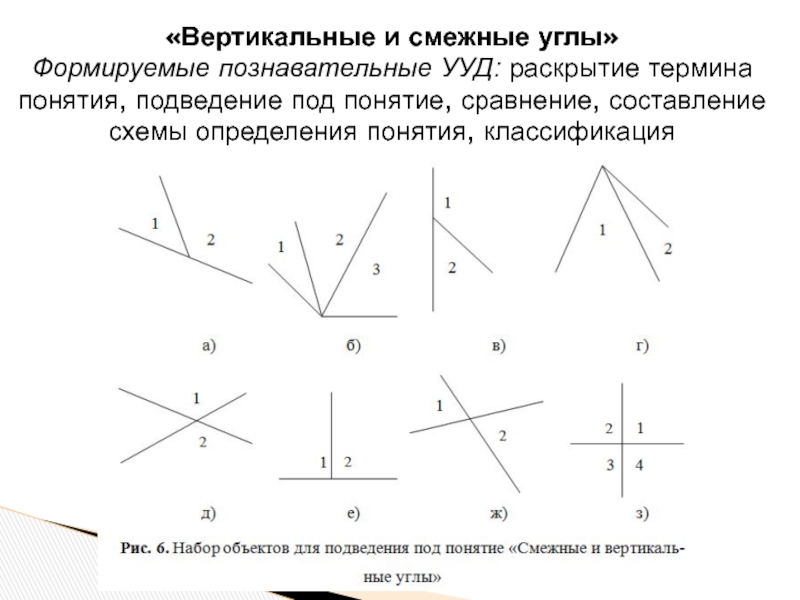
Слайд 11«Вертикальные и смежные углы»
Формируемые познавательные УУД: раскрытие термина понятия, подведение под
Слайд 12 1. Раскройте термины понятий «Угол», «Биссектриса угла» (памятка «Раскрытие термина понятия»). 2.
Слайд 13«Свойства смежных и вертикальных углов»
Формируемые познавательные УУД: анализ формулировки теоремы, выведение
1. Прочитайте формулировку теоремы о смежных углах в учебнике. Переформулируйте свойство смежных углов в терминах «если…то». Проверьте ответ, используя данную схему.
2. Поменяйте местами условие и требование теоремы: «Сумма смежных углов равна 180°», оставив разъяснительную часть без изменения, и попробуйте сформулировать новое – «обратное» утверждение. Является ли это утверждение верным?
Слайд 14«Равнобедренный треугольник»
Формируемые познавательные УУД: пошаговая запись решения, выбор метода решения задачи,
Выполнить доказательство аналитическим методом, изобразить граф-схему и записать по шагам решение.
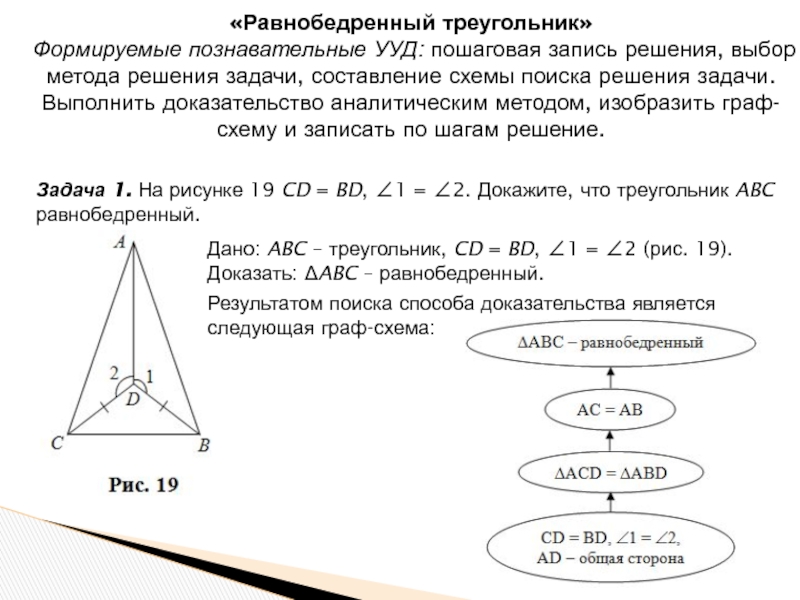
Задача 1. На рисунке 19 CD = BD, 1 = 2. Докажите, что треугольник ABC равнобедренный.
Дано: ABC – треугольник, CD = BD, 1 = 2 (рис. 19).
Доказать: ABC – равнобедренный.
Результатом поиска способа доказательства является следующая граф-схема:
Слайд 15«Равнобедренный треугольник»
Формируемые познавательные УУД: пошаговая запись решения, выбор метода решения задачи,
Выполнить доказательство аналитическим методом, изобразить граф-схему и записать по шагам решение.
Задача 1. На рисунке 19 CD = BD, 1 = 2. Докажите, что треугольник ABC равнобедренный.
Дано: ABC – треугольник, CD = BD, 1 = 2 (рис. 19).
Доказать: ABC – равнобедренный.
Пошаговая запись доказательства:
1. Рассмотрим ACD и ABD. Так как CD = BD, 1 = 2 и AD – общая сторона, то по 1 признаку равенства треугольников ACD = ABD.
2. ACD = ABD AC = AB.
3. Значит ABC – равнобедренный.
Вывод: ч. т. д.
Слайд 16Задача . По данным рисунка 25 найдите NSB.
«Параллельные прямые»
Формируемые познавательные
Выполнить доказательство задачи, изобразить граф-схему и записать пошаговое решение.
Дано: прямые AB и CD,
ME и NK – секущие, MPS = 73°, COP = 107°, STD = 92° (рис. 25).
Найти: NSB.
Решение:
Слайд 17Задача . По данным рисунка 25 найдите NSB.
«Параллельные прямые»
Формируемые познавательные
Выполнить доказательство задачи, изобразить граф-схему и записать пошаговое решение.
Дано: прямые AB и CD,
ME и NK – секущие, MPS = 73°, COP = 107°, STD = 92° (рис. 25).
Найти: NSB.
Пошаговая запись решения:
1. APO = MPS как вертикальные, значит, APO = 73°.
2. COP + APO = 73° + 107° = 180°, а COP + APO – односторонние при прямых AB и CD и секущей ME, значит, AB || CD.
3. Так как AB || CD, то NSB = STD, , NSB = 92°.
Ответ: 92°.
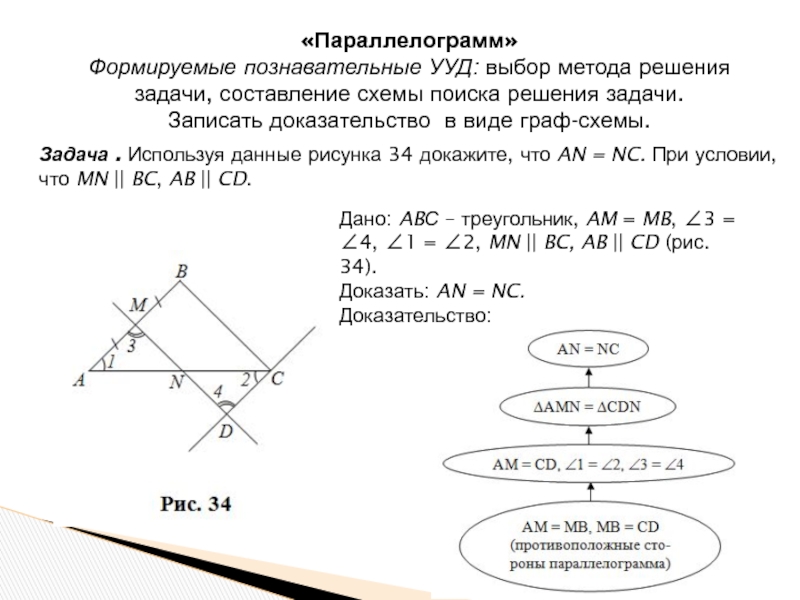
Слайд 18Задача . Используя данные рисунка 34 докажите, что AN = NC.
«Параллелограмм»
Формируемые познавательные УУД: выбор метода решения задачи, составление схемы поиска решения задачи.
Записать доказательство в виде граф-схемы.
Дано: ABС – треугольник, AM = MB, 3 = 4, 1 = 2, MN || BC, AB || CD (рис. 34).
Доказать: AN = NC.
Доказательство: