Пусть одно движение переводит точку A в точку A', а другое движение переводит точку A' в точку A''. Тогда преобразование плоскости, при котором точке A сопоставляется точка A'', называется композицией движений. Оно получается последовательным выполнением двух данных движений.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Движение - материалы к уроку.
Содержание
- 1. Движение - материалы к уроку.
- 2. СвойстваСвойство 1. Композиция движений является движением.Свойство 2.
- 3. Равенство фигурДве фигуры называются равными, если они
- 4. Вопрос 1Какое преобразование плоскости называется движением?Ответ: Движением называется преобразование плоскости, сохраняющее расстояния между точками.
- 5. Вопрос 2Приведите примеры движений. Ответ: Примерами движений являются: центральная симметрия, поворот, осевая симметрия и параллельный перенос.
- 6. Вопрос 3Что называется композицией движений?Ответ: Композицией движений
- 7. Вопрос 4Какие фигуры называются равными?Ответ: Две фигуры называются равными, если они движением переводятся одна в другую.
- 8. Вопрос 5Как обозначается равенство фигурОтвет: Равенство фигур F и F’ обозначается F = F’.
- 9. Упражнение 1Могут ли при движении разные точки переходить в одну точку?Ответ: Нет.
- 10. Упражнение 2Могут ли при движении разные прямые переходить в одну прямую?Ответ: Нет.
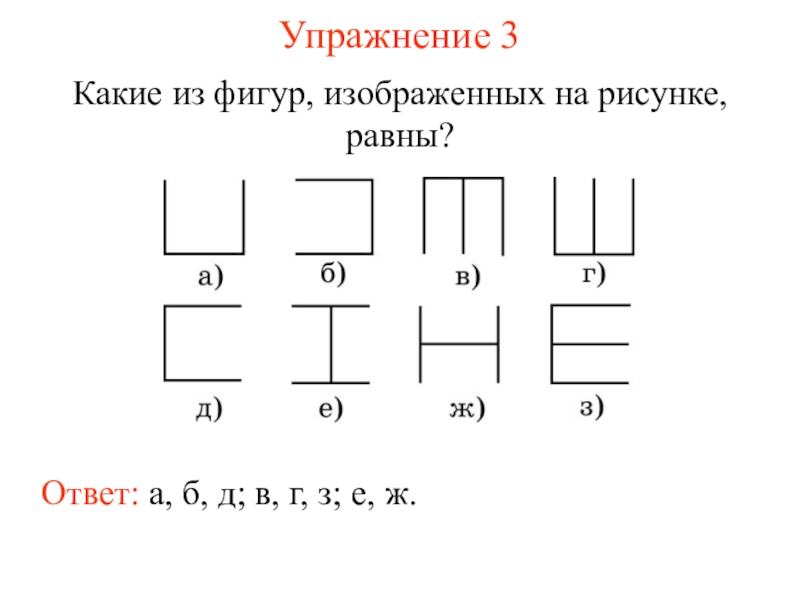
- 11. Упражнение 3Какие из фигур, изображенных на рисунке,
- 12. Упражнение 4Для лучей, изображенных на рисунке, укажите
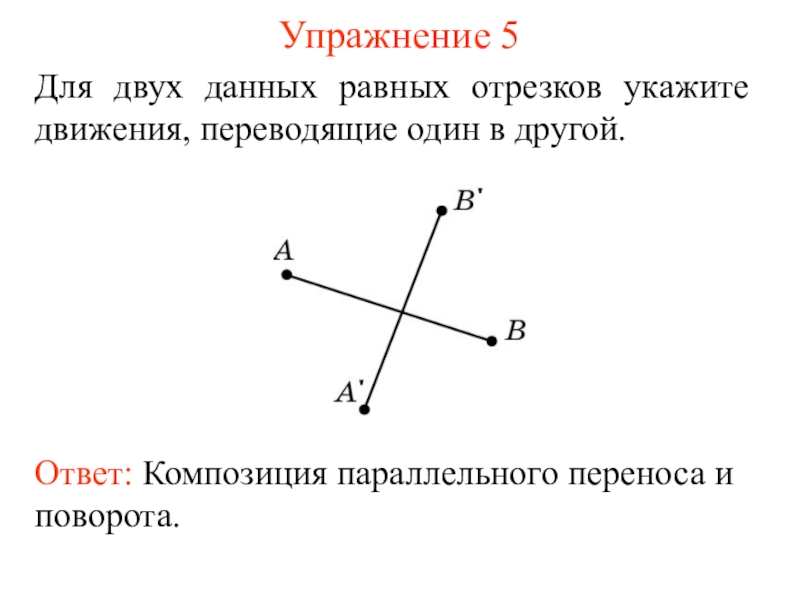
- 13. Упражнение 5Ответ: Композиция параллельного переноса и поворота.Для
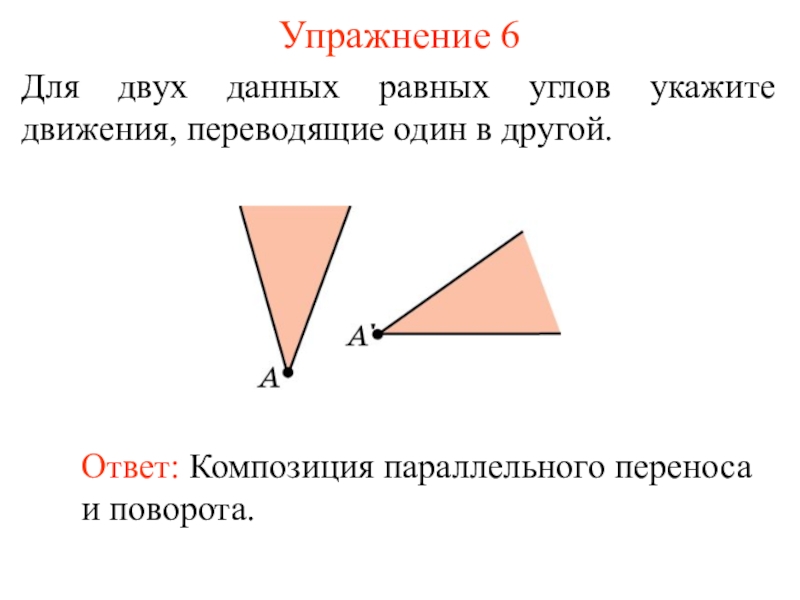
- 14. Упражнение 6Для двух данных равных углов укажите
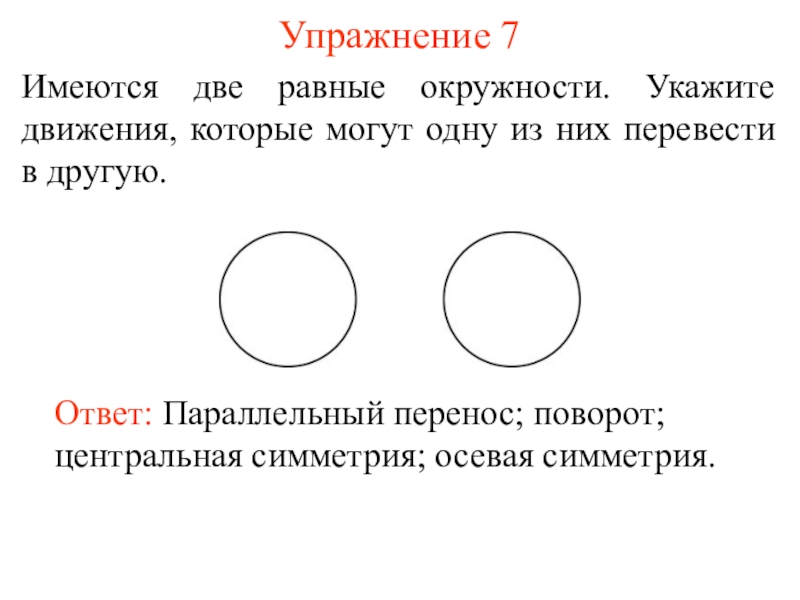
- 15. Упражнение 7Имеются две равные окружности. Укажите движения,
- 16. Упражнение 8Назовите движения, при которых каждая прямая
- 17. Упражнение 9*Каким движением можно заменить две последовательно выполненные осевые симметрии относительно параллельных прямых?Ответ: Параллельным переносом.
- 18. Упражнение 10*Верно ли следующее утверждение: «Если движение
СвойстваСвойство 1. Композиция движений является движением.Свойство 2. Движение переводит прямые в прямые, лучи в лучи и отрезки в отрезки (рис. 1).Свойство 3. При движении сохраняются углы (рис. 2).
Слайд 1Движение
Движением называется преобразование плоскости, сохраняющее расстояния между точками, т.е. если точки
А, В переводятся в точки А', B' соответственно, то АВ = A'B'. Примерами движений являются: центральная симметрия, поворот, осевая симметрия и параллельный перенос.
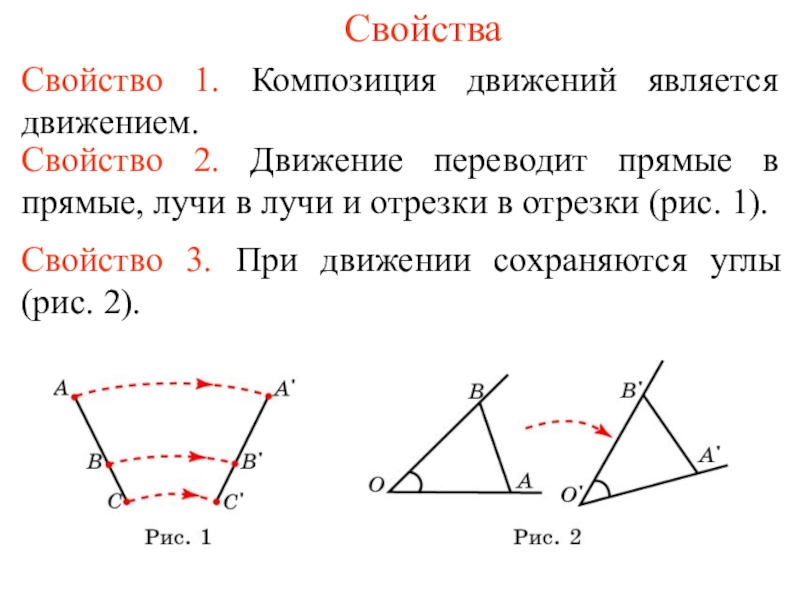
Слайд 2Свойства
Свойство 1. Композиция движений является движением.
Свойство 2. Движение переводит прямые в
прямые, лучи в лучи и отрезки в отрезки (рис. 1).
Свойство 3. При движении сохраняются углы (рис. 2).
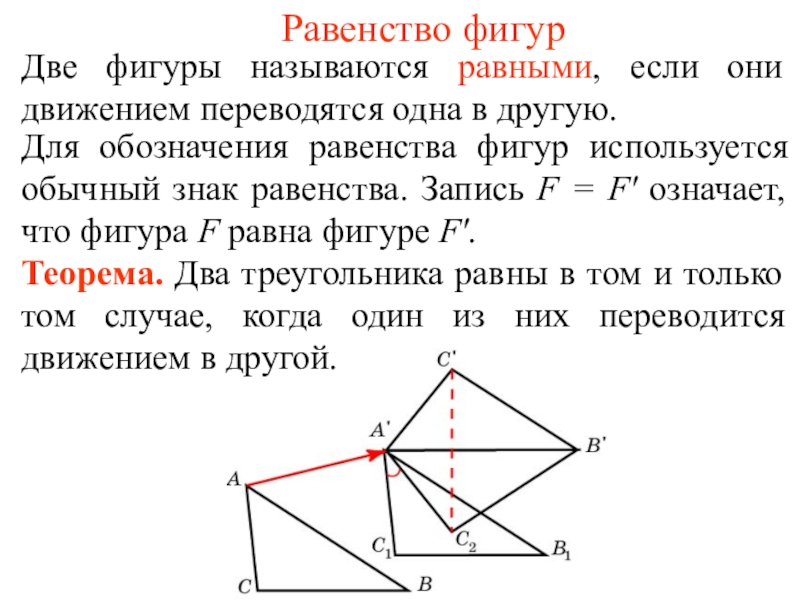
Слайд 3Равенство фигур
Две фигуры называются равными, если они движением переводятся одна в
другую.
Для обозначения равенства фигур используется обычный знак равенства. Запись F = F' означает, что фигура F равна фигуре F'.
Теорема. Два треугольника равны в том и только том случае, когда один из них переводится движением в другой.
Слайд 4Вопрос 1
Какое преобразование плоскости называется движением?
Ответ: Движением называется преобразование плоскости, сохраняющее
расстояния между точками.
Слайд 5Вопрос 2
Приведите примеры движений.
Ответ: Примерами движений являются: центральная симметрия, поворот,
осевая симметрия и параллельный перенос.
Слайд 6Вопрос 3
Что называется композицией движений?
Ответ: Композицией движений называется преобразование, получающееся в
результате последовательных выполнений двух данных движений.
Слайд 7Вопрос 4
Какие фигуры называются равными?
Ответ: Две фигуры называются равными, если они
движением переводятся одна в другую.
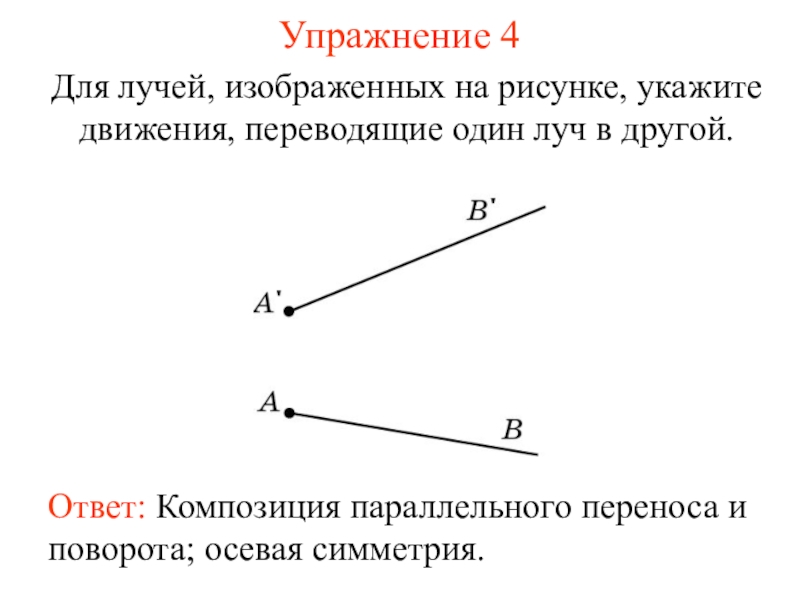
Слайд 12Упражнение 4
Для лучей, изображенных на рисунке, укажите движения, переводящие один луч
в другой.
Ответ: Композиция параллельного переноса и поворота; осевая симметрия.
Слайд 13Упражнение 5
Ответ: Композиция параллельного переноса и поворота.
Для двух данных равных отрезков
укажите движения, переводящие один в другой.
Слайд 14Упражнение 6
Для двух данных равных углов укажите движения, переводящие один в
другой.
Ответ: Композиция параллельного переноса и поворота.
Слайд 15Упражнение 7
Имеются две равные окружности. Укажите движения, которые могут одну из
них перевести в другую.
Ответ: Параллельный перенос; поворот; центральная симметрия; осевая симметрия.
Слайд 16Упражнение 8
Назовите движения, при которых каждая прямая переходит в параллельную ей
прямую или в себя.
Ответ: Параллельный перенос; центральная симметрия.
Слайд 17Упражнение 9*
Каким движением можно заменить две последовательно выполненные осевые симметрии относительно
параллельных прямых?
Ответ: Параллельным переносом.
Слайд 18Упражнение 10*
Верно ли следующее утверждение: «Если движение G оставляет точки A
и B на месте, то G является осевой симметрией»?
Ответ: Да.
