- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Длина дуги. Единичные векторы касательной, главные нормали и бинормали
Содержание
- 1. Длина дуги. Единичные векторы касательной, главные нормали и бинормали
- 2. Под длиной дуги AB понимается предел, к которому стремится
- 3. Кривая называется гладкой, если она непрерывна и в каждой
- 4. Рассмотрим i -тое звено ломаной , где - приращение функции f(x) на . Согласно
- 5. Пример: Найти длину дуги кривой между точками с
- 6. Рис. В точке кривой построены векторы касательной
- 7. Прямая, перпендикулярная касательной и проходящая через точку
- 8. Векторное уравнение бинормали в точке, отвечающей значению t0 параметра t, имеет вид:
- 9. Направление главной нормали может быть получено как двойное векторное произведение:
- 10. Для плоской кривой содержащая её плоскость совпадает
Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена стремится к нулю.
Слайд 2Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной
в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена стремится
к нулю.
к нулю.
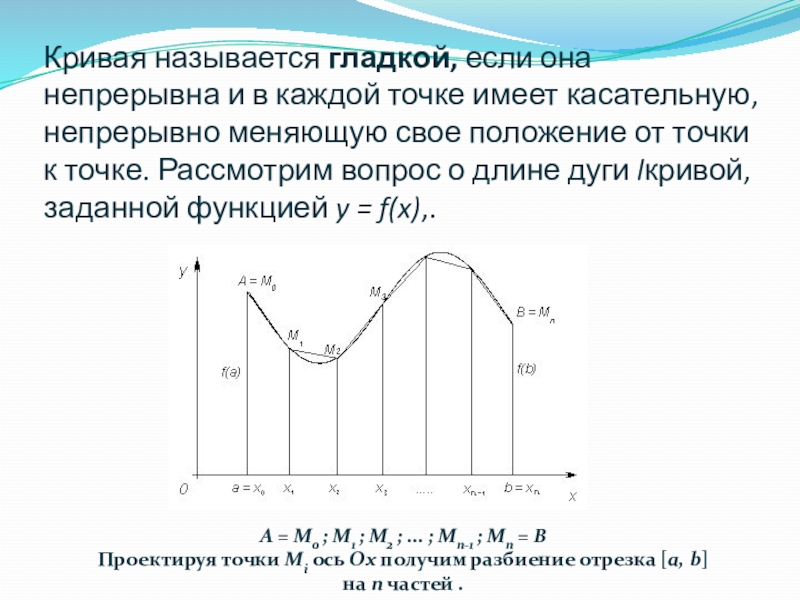
Слайд 3Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную, непрерывно
меняющую свое положение от точки к точке. Рассмотрим вопрос о длине дуги lкривой, заданной функцией y = f(x),.
A = M0 ; M1 ; M2 ; ... ; Mn-1 ; Mn = B
Проектируя точки Mi ось Ox получим разбиение отрезка [a, b] на n частей .
Слайд 4
Рассмотрим i -тое звено ломаной , где - приращение функции f(x) на .
Согласно теореме Лагранжа:
Тогда:
,
а длину всей ломаной можно получить суммируя все её звенья.
Перейдем к пределу, считая, что длина наибольшего звена стремится к нулю.
а длину всей ломаной можно получить суммируя все её звенья.
Перейдем к пределу, считая, что длина наибольшего звена стремится к нулю.
,
Слайд 5Пример: Найти длину дуги кривой между точками с абсциссами x1 = 3 и x2 =
8.
Согласно формуле,имеем:
Слайд 6Рис. В точке кривой построены векторы касательной (T), главной нормали (N)
и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.
Единичные векторы касательной, главные нормали и бинормали
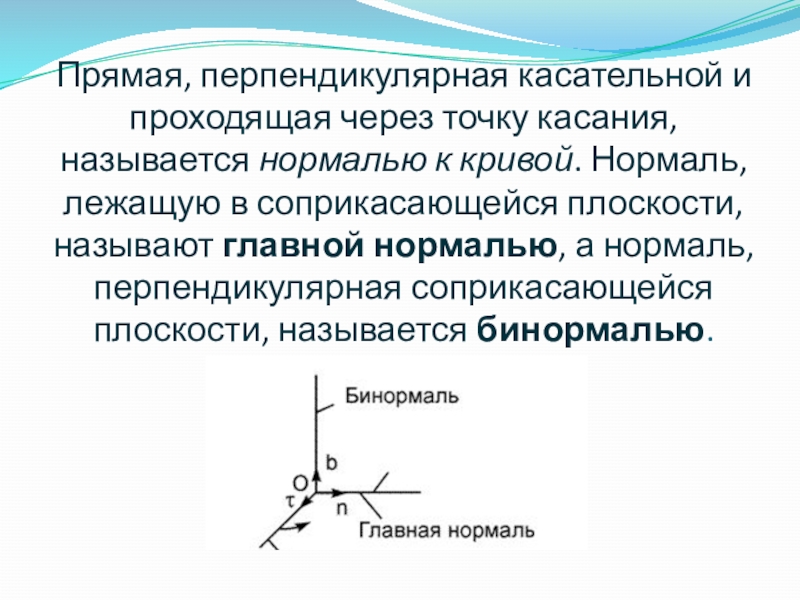
Слайд 7Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью.
Слайд 10Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с
точностью до знака, только одна — главная, и её уравнение в точке имеет следующий вид: