№ 31 Г. Тверь
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему 5 уроков по геометрии.Сумма углов треугольника
Содержание
- 1. 5 уроков по геометрии.Сумма углов треугольника
- 2. УРОК 1
- 3. В Атлантическом океане есть место, по форме
- 4. Слайд 4
- 5. Вспомним, какая фигура называется треугольником? Треугольник –
- 6. Теперь вспомним какие виды углов мы знаем.1
- 7. Виды треугольников Запишем в тетрадь:Выделяют следующие виды
- 8. Сделаем чертежи
- 9. По числу равных сторонРавнобедренным называется треугольник, у
- 10. Теорема: СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180°ПЛАН ДОКАЗАТЕЛЬСТВА:Построим
- 11. Дано: ∆ АВС; Доказать:
- 12. ЗадачаДано: ∆ АВС;
- 13. Решение задач
- 14. Слайд 14
- 15. Параграф 1 читать. Знать виды треугольников. Учить
- 16. Слайд 16
- 17. УРОК 2
- 18. Вам были заданы номера № 223 №225 №226ПРОВЕРИМОткройте тетради с домашней работой
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Теперь повторим теорию 1. Какие
- 23. Сегодня мы познакомимся с понятием внешний угол треугольника
- 24. Какие углы называются смежными углами?Два угла у
- 25. Построим треугольник АВС. Продолжим сторону АС за
- 26. Сколько внешних углов треугольника может быть при
- 27. Угол 4 – внешний угол треугольникаУгол 5
- 28. Слайд 28
- 29. ЗАДАЧАВнешний угол треугольника АВС при вершине В
- 30. ЗАДАЧАТреугольник АВС равнобедренный с основанием АС. Внешний
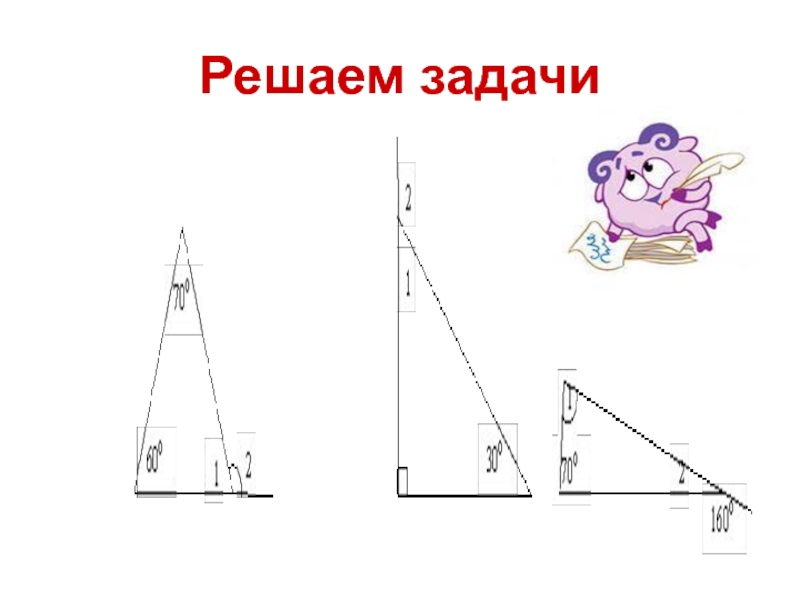
- 31. Решаем задачи
- 32. ДОМАШНЯЯ РАБОТА 228 234
- 33. Слайд 33
- 34. УРОК 3
- 35. РЕШАЕМ ЗАДАЧИ ИЗ ГИА
- 36. Решение: Так как АВ =ВС, то треугольник
- 37. Слайд 37
- 38. Самостоятельно решите задачу В треугольнике ABC угол
- 39. Слайд 39
- 40. Самостоятельно решите задачуВ треугольнике ABC стороны AC
- 41. Два угла треугольника МНК равны 27 и
- 42. Сдаем тетради с классной работой!!!
- 43. ДОМАШНЯЯ РАБОТА
- 44. УРОК 4
- 45. УСТНООдин из внешних углов треугольника равен 95°.
- 46. Повторим…Сумма углов треугольника равна … .Треугольник, у
- 47. Теорема о соотношении между сторонами и углами
- 48. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ:Следствие 1: В прямоугольном треугольнике
- 49. НЕРАВЕНСТВО ТРЕУГОЛЬНИКАФормулировка теоремы: Каждая сторона треугольника меньше суммы двух других сторон.
- 50. . Следствие : для любых трёх точек А,В,С, не лежащих на одной прямой, справедливы неравенства:АВ
- 51. Закрепление изученного материала В треугольнике АВС: С=А=В.
- 52. 1) Существует ли треугольник со сторонами:10см, 15см, 2см (нет,т.к. 2см+10см5см).Объясните ответ.
- 53. ЗадачаГрадусные меры углов А и В треугольника
- 54. Решение. Сумма внешних углов треугольника равна 360
- 55. ДОМАШЯЯ РАБОТА №1 Один из углов треугольника
- 56. УРОК 5
- 57. САМОСТОЯТЕЛЬНАЯ РАБОТА
- 58. Задача
- 59. Диагональ параллелограмма образует с двумя его сторонами
УРОК 1
Слайд 3В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о
которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется «бермудским треугольником». А ещё его называют «дьявольский треугольник», «треугольник проклятых». Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа «бермудского треугольника» остаётся тайной и по сей день.
Слайд 5Вспомним, какая фигура называется треугольником?
Треугольник – это это геометрическая фигура,
образованная
тремя отрезками,
которые соединяют три не лежащие
на одной прямой точки.
Три точки, образующие треугольник,
называются вершинами треугольника,
а отрезки — сторонами треугольника.
которые соединяют три не лежащие
на одной прямой точки.
Три точки, образующие треугольник,
называются вершинами треугольника,
а отрезки — сторонами треугольника.
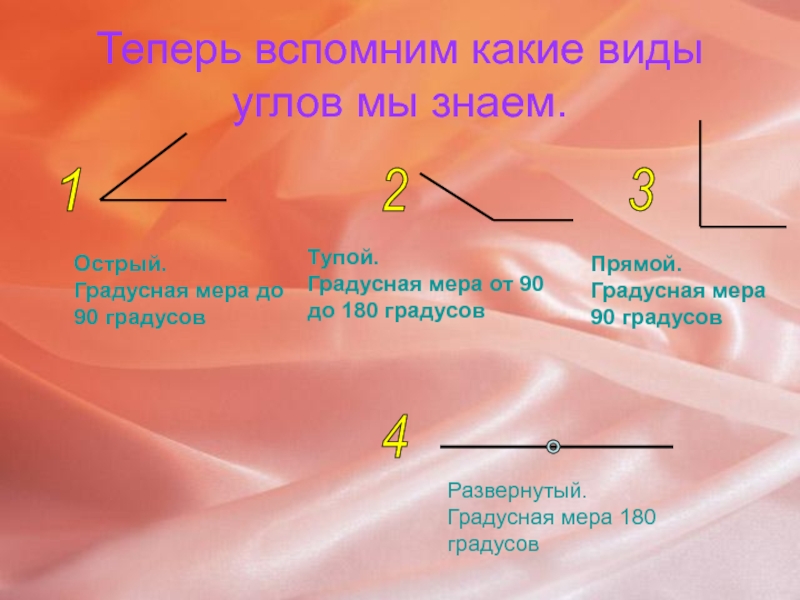
Слайд 6Теперь вспомним какие виды углов мы знаем.
1
2
3
4
Развернутый.
Градусная
мера 180 градусов
Острый.
Градусная мера до 90 градусов
Тупой.
Градусная мера от 90
до 180 градусов
Прямой.
Градусная мера 90 градусов
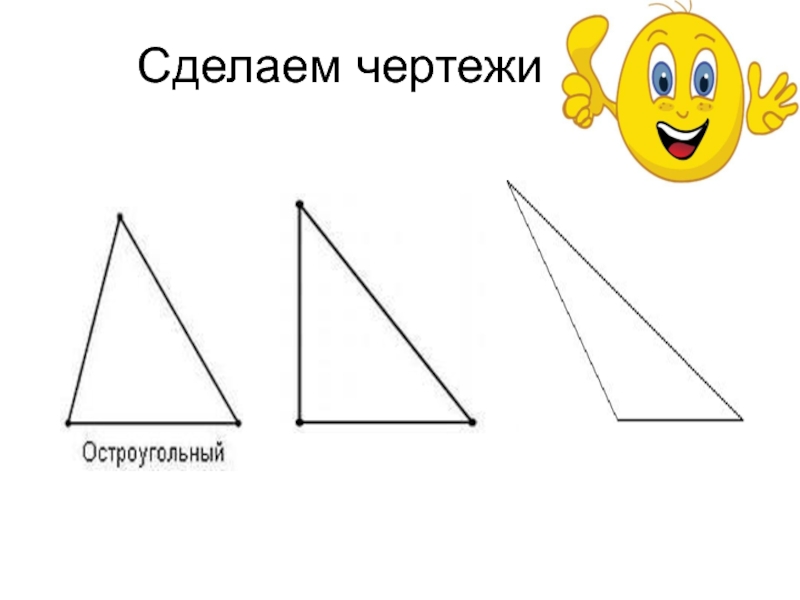
Слайд 7Виды треугольников
Запишем в тетрадь:
Выделяют следующие виды треугольников:
Если все углы треугольника острые,
то треугольник называется остроугольным;
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Слайд 9По числу равных сторон
Равнобедренным называется треугольник, у которого две стороны равны.
Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Слайд 10Теорема: СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180°
ПЛАН ДОКАЗАТЕЛЬСТВА:
Построим произвольный треугольник.
Проведем прямую через
одну из вершин противолежащей стороне.
Составим пары равных углов, вспомнив теоремы об углах, образованных параллельными прямыми.
Представим развернутый уго в виде суммы углов.
Заменим слагаемые равным им углам треугольника.
Составим пары равных углов, вспомнив теоремы об углах, образованных параллельными прямыми.
Представим развернутый уго в виде суммы углов.
Заменим слагаемые равным им углам треугольника.
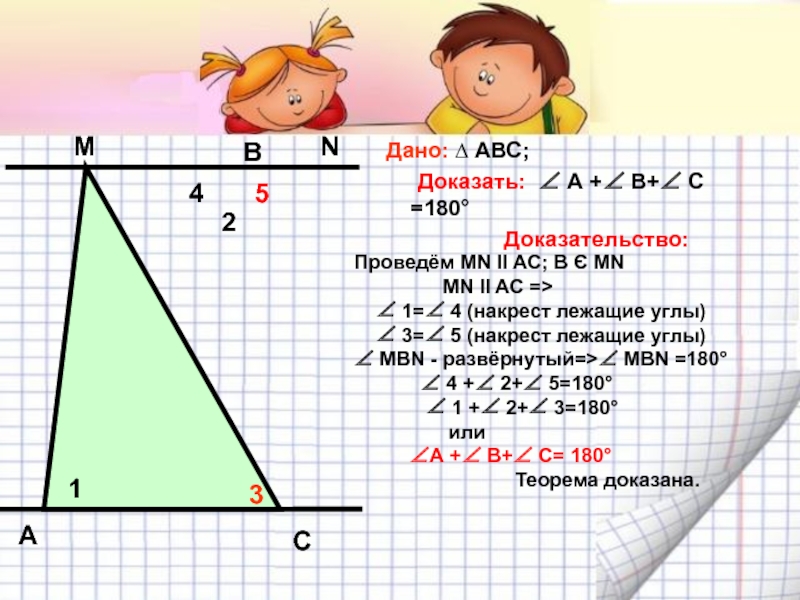
Слайд 11 Дано: ∆ АВС;
Доказать: ∠ А +∠ В+∠
С =180°
Доказательство:
Доказательство:
Проведём MN II AC; В Є МN
MN II AC =>
∠ 1=∠ 4 (накрест лежащие углы)
∠ 3=∠ 5 (накрест лежащие углы)
∠ МВN - развёрнутый=>∠ МВN =180°
∠ 4 +∠ 2+∠ 5=180°
∠ 1 +∠ 2+∠ 3=180°
или
∠А +∠ В+∠ С= 180°
Теорема доказана.
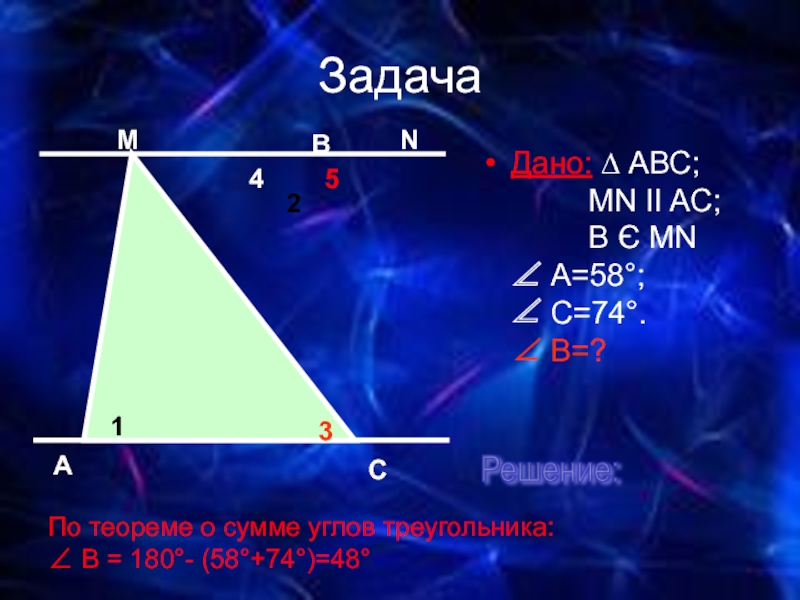
Слайд 12Задача
Дано: ∆ АВС;
MN II AC;
В Є МN
∠ А=58°;
∠ С=74°.
∠ В=?
Решение:
По теореме о сумме углов треугольника: ∠ В = 180°- (58°+74°)=48°
Слайд 15Параграф 1 читать. Знать виды треугольников. Учить теорему о сумме углов
треугольника с доказательством
№ 223 №225 №226
№ 223 №225 №226
ДОМАШНЕЕ ЗАДАНИЕ
Слайд 22Теперь повторим теорию 1. Какие виды треугольников вы знаете? 2. Как звучит теорема
о сумме углов треугольников?
Слайд 24Какие углы называются смежными углами?
Два угла у которых одна сторона общая,
а две другие являются продолжением друг друга.
Слайд 25
Построим треугольник АВС.
Продолжим сторону АС за вершину С.
Образовался угол 4.
Каким он является по отношению к углу 3?
А
В
С
4
3
ОПРЕДЕЛЕНИЕ:
Угол, смежный с каким-нибудь углом треугольника, называется ВНЕШНИМ УГЛОМ треугольника.
Слайд 26Сколько внешних углов треугольника может быть при каждой вершине треугольника? Что
нужно сделать, чтобы построить внешний угол.
Слайд 27Угол 4 – внешний угол треугольника
Угол 5 внешний угол треугольника. Вспомним
теорему о сумме углов треугольника.
1 + 2 + 3 = 180
2 + 4 = 180
1 + 2 + 3 = 2 + 4;
4 = 1 + 2 + 3 – 2;
4 = (1 + 2) + 2 – 2;
4 = 1 + 2;
1 + 2 + 3 = 180
2 + 4 = 180
1 + 2 + 3 = 2 + 4;
4 = 1 + 2 + 3 – 2;
4 = (1 + 2) + 2 – 2;
4 = 1 + 2;
1
2
3
4
5
ВЫВОД: Внешний угол треугольника равен сумме углов треугольника не смежных с ним!!!
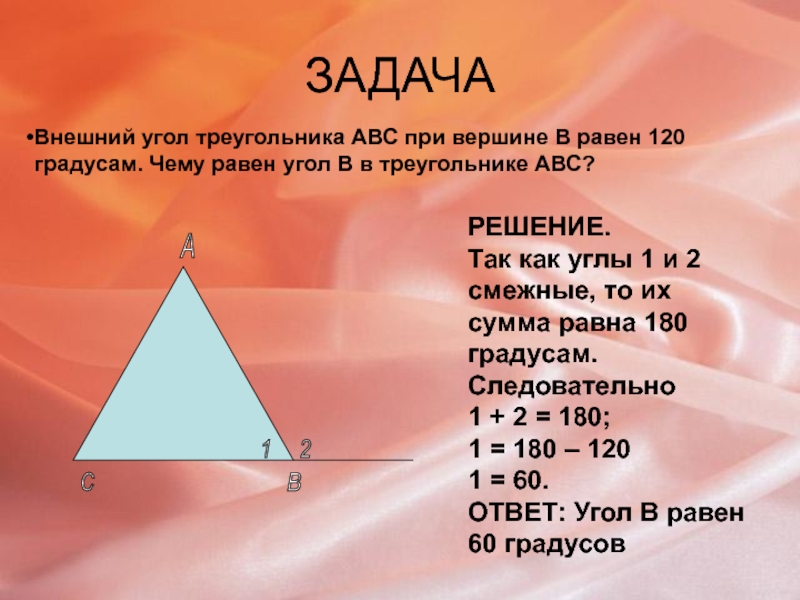
Слайд 29ЗАДАЧА
Внешний угол треугольника АВС при вершине В равен 120 градусам. Чему
равен угол В в треугольнике АВС?
РЕШЕНИЕ.
Так как углы 1 и 2 смежные, то их сумма равна 180 градусам. Следовательно
1 + 2 = 180;
1 = 180 – 120
1 = 60.
ОТВЕТ: Угол В равен 60 градусов
В
С
А
1 2
Слайд 30ЗАДАЧА
Треугольник АВС равнобедренный с основанием АС. Внешний угол при вершине В
равен 100 градусов. Чему равен угол А и угол В.
А
С
В
100
РЕШЕНИЕ:
Угол DВС – внешний угол.
DВС = А + С ( по свойству внешнего угла)
100 = А + С
Треугольник АВС равнобедренный по условию. В равнобедренном треугольнике углы при основании равны, значит А = С = х
100 = х + х;
100 = 2х;
2х = 100;
Х = 100/2
Х = 50
ОТВЕТ: А = 50; С = 50.
Слайд 36Решение: Так как АВ =ВС, то треугольник равнобедренный. Следовательно углы при
основании равны, значит, А = С ;
Угол А дан по условию и равен 55 градусов, следовательно и угол С = 55.
По теореме о сумме углов треугольника находим угол В. А + В + С = 180; В = 180 – 55 – 55; В = 70.
ОТВЕТ: УГОЛ В = 70 ГРАДУСОВ,
Угол А дан по условию и равен 55 градусов, следовательно и угол С = 55.
По теореме о сумме углов треугольника находим угол В. А + В + С = 180; В = 180 – 55 – 55; В = 70.
ОТВЕТ: УГОЛ В = 70 ГРАДУСОВ,
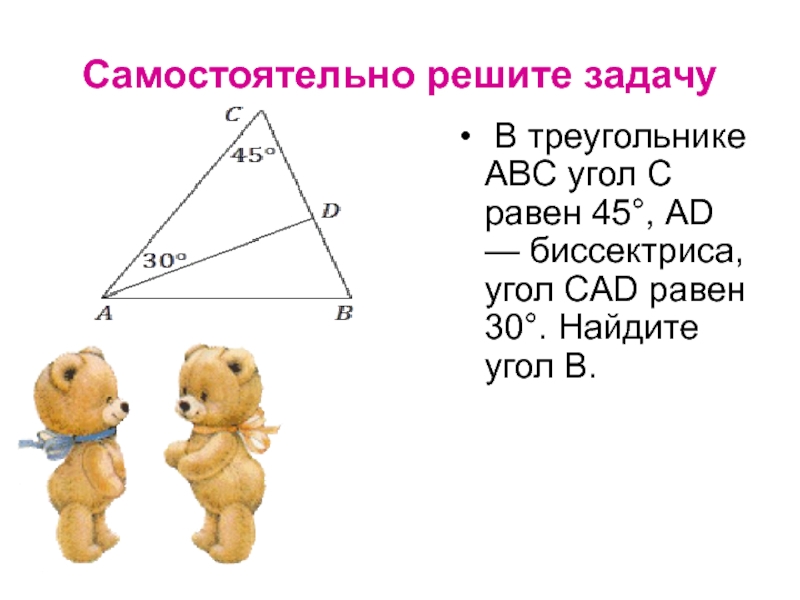
Слайд 38Самостоятельно решите задачу
В треугольнике ABC угол C равен 45°, AD
— биссектриса, угол CAD равен 30°. Найдите угол B.
Слайд 40Самостоятельно решите задачу
В треугольнике ABC стороны AC = BC, угол C
равен 40°. Найдите внешний угол DBC.
Слайд 41Два угла треугольника МНК равны 27 и 63 градуса. Найдите разность
градусных мер большего и меньшего углов этого треугольника.
РЕШЕНИЕ. Пусть известно, что в треугольнике МНК М = 27, н = 63.
Тогда К = 180 – ( М + К) = 180 – (27 + 63) = 90.
Значит в треугольнике МНК наибольшим является угол К = 90;, а наименьшим угол М = 27.
Поэтому разность градусных мер большего и меньшего углов этого треугольника равна: 90 – 27 = 63 градуса.
Ответ: 63 градуса.
Слайд 45УСТНО
Один из внешних углов треугольника равен 95°. Чему равна сумма двух
внутренних углов, с ним не смежных?
Слайд 46Повторим…
Сумма углов треугольника равна … .
Треугольник, у которого есть прямой угол,
называется Гипотенузой прямоугольного треугольника называется … , другие стороны называются … .
Треугольник, в котором есть тупой угол, называется …
Угол, смежный с внутренним углом треугольника, называется …
Внешний угол треугольника равен … .
В треугольнике против большего угла лежит … сторона, а против большей стороны лежит … угол.
Треугольник, в котором есть тупой угол, называется …
Угол, смежный с внутренним углом треугольника, называется …
Внешний угол треугольника равен … .
В треугольнике против большего угла лежит … сторона, а против большей стороны лежит … угол.
Слайд 47Теорема о соотношении между сторонами и углами треугольника
В треугольнике:
1)
против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
2) против большего угла лежит большая сторона.
Слайд 48СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ:
Следствие 1: В прямоугольном треугольнике гипотенуза больше любого катета.
Следствие 2: Если два угла треугольника равны, то стороны треугольника, лежащие против этих углов, тоже равны.
Слайд 49НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Формулировка теоремы:
Каждая сторона треугольника меньше суммы двух других сторон.
Слайд 50. Следствие : для любых трёх точек А,В,С, не лежащих на
одной прямой, справедливы неравенства:
АВ<АС+СВ;
АС<АВ+ВС;
ВС<ВА+АС.
Каждое из этих неравенств называется неравенством треугольника.
Выводы:
1) В треугольнике:
Против большей стороны лежит больший угол и, наоборот, против большего угла лежит большая сторона;
Если стороны равны, то равны и углы, лежащие против них, и наоборот, если углы равны, то стороны, лежащие против этих углов, тоже равны.
АВ<АС+СВ;
АС<АВ+ВС;
ВС<ВА+АС.
Каждое из этих неравенств называется неравенством треугольника.
Выводы:
1) В треугольнике:
Против большей стороны лежит больший угол и, наоборот, против большего угла лежит большая сторона;
Если стороны равны, то равны и углы, лежащие против них, и наоборот, если углы равны, то стороны, лежащие против этих углов, тоже равны.
Слайд 51Закрепление изученного материала
В треугольнике АВС: С=А=В. Что это за треугольник?
Треугольник
АСВ – тупоугольный треугольник. Его угол С – тупой. Какая из сторон этого треугольника самая большая?
Возможно ли, что прямоугольный треугольник будет и равнобедренный?
Возможно ли, что прямоугольный треугольник будет и равнобедренный?
Слайд 521) Существует ли треугольник со сторонами:
10см, 15см, 2см
(нет,т.к. 2см+10см
3см
(нет, т.к. 1см+2см=3см);
2см, 2см, 4см
(нет, т.к. 2см+2см=4см);
3см, 4см, 5см
(да, т.к. 3см+4см>5см).
Объясните ответ.
(нет, т.к. 1см+2см=3см);
2см, 2см, 4см
(нет, т.к. 2см+2см=4см);
3см, 4см, 5см
(да, т.к. 3см+4см>5см).
Объясните ответ.
Слайд 53Задача
Градусные меры углов А и В треугольника относятся как 36:29. Найдите
градусную меру угла С, если известно, что градусные меры всех углов треугольника выражаются целыми числами градусов.
РЕШЕНИЕ, Пусть градусные меры углов А,В и С находятся в отношении 36:29:х, то есть их градусные меры равны соответственно 36*k, 29*k, x*k, где k – натуральное число ( 36 и 29 – взаимно просты.) Тогда имеем:
36*k+29*k+x*k = 180 k = 180/(36 +29+х)
Так как 36+29+х>60 и k натуральное число, то
Либо 36+29+х = 90, либо 36+29+х = 180.
Если 36+29+х = 90, то х = 25, k = 2, угол С = 50
Если 36+29+х = 180, то х = 115, K = 1, угол С = 115.
РЕШЕНИЕ, Пусть градусные меры углов А,В и С находятся в отношении 36:29:х, то есть их градусные меры равны соответственно 36*k, 29*k, x*k, где k – натуральное число ( 36 и 29 – взаимно просты.) Тогда имеем:
36*k+29*k+x*k = 180 k = 180/(36 +29+х)
Так как 36+29+х>60 и k натуральное число, то
Либо 36+29+х = 90, либо 36+29+х = 180.
Если 36+29+х = 90, то х = 25, k = 2, угол С = 50
Если 36+29+х = 180, то х = 115, K = 1, угол С = 115.
Слайд 54Решение. Сумма внешних углов треугольника равна 360 градусам. Получаем:
10*K + 9*K
+ 5*K = 360;
24K = 360;
К = 360/24
K =15 Значит внешние углы равны 15*10 = 150; 15* 9= 135; 15* 5 = 75;
Соответственно углы треугольника равны:
180- 135 = 45; 180 – 150 = 30; 180 – 75 = 105.
24K = 360;
К = 360/24
K =15 Значит внешние углы равны 15*10 = 150; 15* 9= 135; 15* 5 = 75;
Соответственно углы треугольника равны:
180- 135 = 45; 180 – 150 = 30; 180 – 75 = 105.
Слайд 55ДОМАШЯЯ РАБОТА №1 Один из углов треугольника в три раза больше второго
угла и на 5 раз меньше третьего. Найдите углы треугольника.
№2 Найдите углы треугольника, если их градусные меры относятся как 3 : 6 : 11
№3 Два внешних угла треугольника относятся как 1:2 и угол при третьей вершине равен 30 градусов. Найдите неизвестные углы треугольника.
Слайд 59Диагональ параллелограмма образует с двумя его сторонами углы 25° и 35°.
Найдите больший угол параллелограмма.
Решение
Обозначим параллелограмм за ABCD, причем AC — та самая диагональ. Предположим, угол CAD равен 35°, а угол DCA равен 25°. Заметим, что углы BAC и DCA равны: BAC = DCA = 25°. Ведь это внутренние накрест лежащие углы при параллельных прямых AB и CD и секущей AC.
Кроме того, угол BAD = BAC + CAD = 25° + 35° = 60°.
Обозначим неизвестный угол D = x. Поскольку ABCD — параллелограмм, имеем:
B = D = x; BCD = BAD = 60.
Но сумма углов четырехугольника равна 360°, поэтому:
BAD + B + BCD + D = 360;
60 + x + 60 + x = 360; 2x + 120 = 360; 2x = 240; x = 120.
Получается, что углы B и D равны 120°, а углы BAD и BCD — 60°.
Требуется найти больший угол — это угол B. Поэтому ответ — 120 градусов.
Ответ 120
