- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение термодинамической задачи методом смысловых опор.
Содержание
- 1. Решение термодинамической задачи методом смысловых опор.
- 2. Условия задачи:Тепловая машина
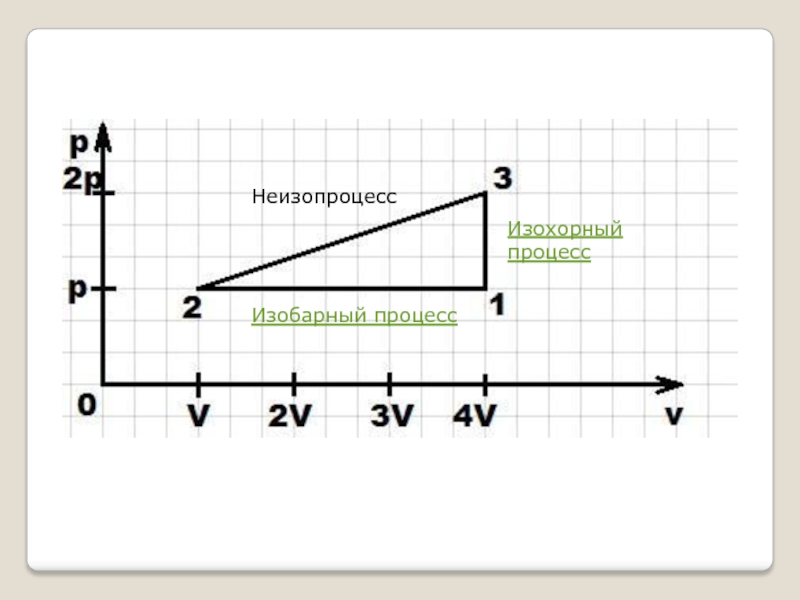
- 3. НеизопроцессИзохорный процессИзобарный процесс
- 4. Решение задачи (1
- 5. 4. Теперь найдем S треугольника 123 =
- 6. Решение вторым способом: Решить задачу можно
- 7. Найдем Q1-2 (Изобарный процесс) A=p△V=p(V2-V1)=p(V-4V)= -3pV
- 8. Слайд 8
- 9. Определения
- 10. Тепловыми маши́нами в термодинамике называются тепловые двигатели и холодильные машины
- 11. Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы
- 12. Изоба́рный проце́сс (др.-греч. «одинаковый» и «тяжесть») — термодинамический процесс, происходящий в системе
- 13. Изохорический или изохорный процесс (от др.-греч. «равный» и «место») — термодинамический процесс, который происходит при
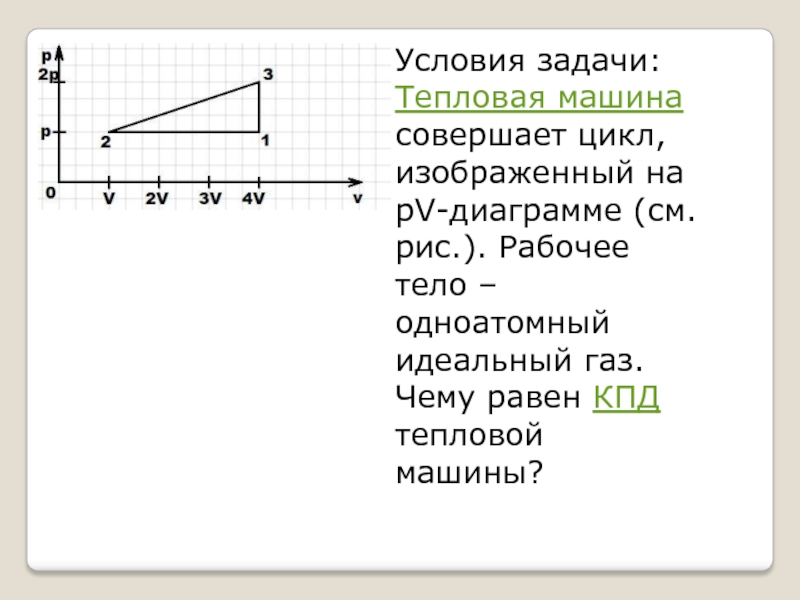
Условия задачи:Тепловая машина совершает цикл, изображенный на рV-диаграмме (см. рис.). Рабочее тело – одноатомный идеальный газ. Чему равен КПД тепловой машины?
Слайд 1Решение термодинамической задачи методом смысловых опор
Учитель физики МБОО
Федотов Виктор Викторович
Слайд 2
Условия задачи:
Тепловая машина совершает цикл, изображенный на
рV-диаграмме (см. рис.). Рабочее тело – одноатомный идеальный газ. Чему равен КПД тепловой машины?
Слайд 4
Решение задачи (1 способ)
Для того, чтобы найти КПД
существует две формулы
и соответственно
два способа
решения этой задачи.
Рассмотрим 1 способ.
В этом способе мы применим первую формулу: Рассмотрим процесс 2-3 1. Найдем работу графика: Аг = S трапеции (S треугольника + S прямоугольника под ним) А = (a+b)/2*h= (p+2p)/2*(4V-V)=3p/2 *3V = 4,5 pV 2. Найдем внутренний процесс: △U = 3/2vR△T= 3/2vR(T2-T1)=3/2(p2V2-p1-V1)=3/2(2p*4V-pV)= 3/2*7pV=21/2=10,5pV 3. Найдем Q=△U+A Q1=10,5pV+4,5pV=15pV
решения этой задачи.
Рассмотрим 1 способ.
В этом способе мы применим первую формулу: Рассмотрим процесс 2-3 1. Найдем работу графика: Аг = S трапеции (S треугольника + S прямоугольника под ним) А = (a+b)/2*h= (p+2p)/2*(4V-V)=3p/2 *3V = 4,5 pV 2. Найдем внутренний процесс: △U = 3/2vR△T= 3/2vR(T2-T1)=3/2(p2V2-p1-V1)=3/2(2p*4V-pV)= 3/2*7pV=21/2=10,5pV 3. Найдем Q=△U+A Q1=10,5pV+4,5pV=15pV
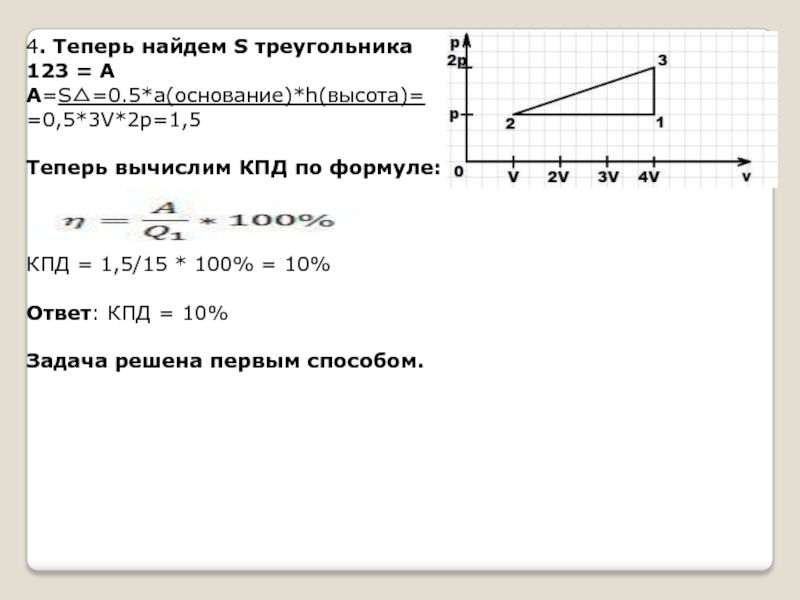
Слайд 54. Теперь найдем S треугольника
123 = А
А=S△=0.5*a(основание)*h(высота)=
=0,5*3V*2p=1,5
Теперь вычислим КПД
по формуле:
КПД = 1,5/15 * 100% = 10%
Ответ: КПД = 10%
Задача решена первым способом.
Слайд 6Решение вторым способом: Решить задачу можно еще по этой формуле: Q1= Q2-3 Q2= Q3-1 +
Q1-2
Найдем Q3-1 (Изохорный процесс)
A=0 т.к. △V=0
△U=3/2vR(T1-T3)=3/2(p1V1-p3V3)=3/2(4pV-2p4V)= 3/2(4pV-8pV)= = 3/2* -4pV= -12/2 = -6
Q3-1= △U1-3+A1-3= -6+0=-6pV Мы нашли Q3-1. Нам осталось найти Q1-2
△U=3/2vR(T1-T3)=3/2(p1V1-p3V3)=3/2(4pV-2p4V)= 3/2(4pV-8pV)= = 3/2* -4pV= -12/2 = -6
Q3-1= △U1-3+A1-3= -6+0=-6pV Мы нашли Q3-1. Нам осталось найти Q1-2
Слайд 7Найдем Q1-2 (Изобарный процесс) A=p△V=p(V2-V1)=p(V-4V)= -3pV △U=3/2vR△T=3/2(p2V2-p1V1)= =3/2(pV-4pV)=3/2* -3= -9/2= =-4,5pV Q1-2= -4,5pV-3pV= -7,5pV Теперь, когда у
нас есть Q3-1 и Q1-2, мы можем найти Q2
Q2= Q3-1+Q1-2= -6-7,5=-13,5
Для того, чтобы нам выразить КПД нам нужно найти А всего цикла:
А цикл. = A2-3+A3-1+A1-2= 4,5+0-3 = 1,5pV
Выражаем КПД: КПД = A/A+Q2 * 100%=1,5/1,5+13,5*100%=
= 0,1*100% = 10%
Ответ: 10%
Задача решена вторым способом.
Слайд 10Тепловыми маши́нами в термодинамике называются тепловые двигатели и холодильные машины (термокомпрессоры) Тепловые двигатели осуществляют превращение тепла
в работу. Для функционирования тепловой машины необходимы следующие составляющие: нагреватель, холодильник и рабочее тело. При этом тепло к рабочему телу подводится от нагревателя, имеющего более высокую температуру , и частично отводится к холодильнику, имеющего более низкую температуру . Необходимость наличия нагревателя и рабочего тела обычно не вызывает сомнений, что же касается холодильника, как конструктивной части тепловой машины, то он может отсутствовать. В этом случае его функцию выполняет окружающая среда.
Слайд 11Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении
преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η. КПД является безразмерной величиной и часто измеряется в процентах.
Формулы для нахождения КПД:
Формулы для нахождения КПД:
Слайд 12Изоба́рный проце́сс (др.-греч. «одинаковый» и «тяжесть») — термодинамический процесс, происходящий в системе при постоянном давлении=const и постоянной массе
газа.
Изобарный процесс в p, v— , T, s— и i, s-координатах (диаграммах)
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа следует:
v/T = R/p = const
или
v2/v1 = T2/T1,
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
l = p(v2 – v1).
Т. к. pv1 = RT1 и pv2 = RT2, то
l = R(T2 – T1).
Количество теплоты при cp = const определяется по формуле:
q = cp(T2 – T1).
Изменение энтропии будет равно:
s2 – s1= Δs = cpln(T2/T1).
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа следует:
v/T = R/p = const
или
v2/v1 = T2/T1,
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
l = p(v2 – v1).
Т. к. pv1 = RT1 и pv2 = RT2, то
l = R(T2 – T1).
Количество теплоты при cp = const определяется по формуле:
q = cp(T2 – T1).
Изменение энтропии будет равно:
s2 – s1= Δs = cpln(T2/T1).
Слайд 13Изохорический или изохорный процесс (от др.-греч. «равный» и «место») — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного
процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.
При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется.
На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T(температура), V (объем) и P (давление). При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
p/T = R/v = const,
т. е. давление газа прямо пропорционально его абсолютной температуре:
p2/p1 = T2/T1.
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
q= cv(T2 — T1).
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Δu = cv(T2 — T1).
Изменение энтропии в изохорном процессе определяется по формуле:
s2 – s1= Δs = cvln(p2/p1) = cvln(T2/T1).
При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется.
На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T(температура), V (объем) и P (давление). При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
p/T = R/v = const,
т. е. давление газа прямо пропорционально его абсолютной температуре:
p2/p1 = T2/T1.
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
q= cv(T2 — T1).
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Δu = cv(T2 — T1).
Изменение энтропии в изохорном процессе определяется по формуле:
s2 – s1= Δs = cvln(p2/p1) = cvln(T2/T1).