- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Раздел 1. Теоретическая механика. Занятие 1. Основные понятия и аксиомы статики
Содержание
- 1. Раздел 1. Теоретическая механика. Занятие 1. Основные понятия и аксиомы статики
- 2. 1.1. Задачи теоретической механикиТеоретическая механика — наука
- 3. 1.2. Понятие о силе и системе силСила
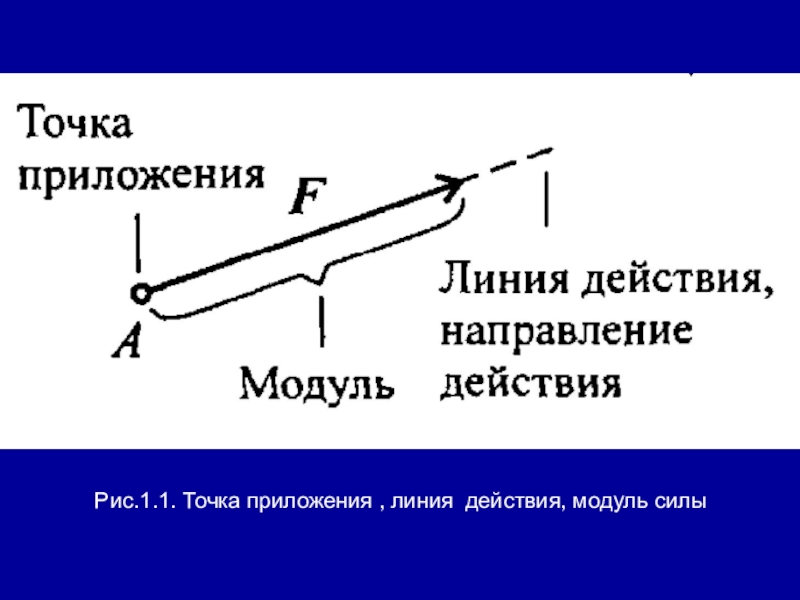
- 4. Рис.1.1. Точка приложения , линия действия, модуль силы
- 5. Силы, действующие на тело (или систему тел),
- 6. Совокупность сил, действующих на какое-либо тело, называют
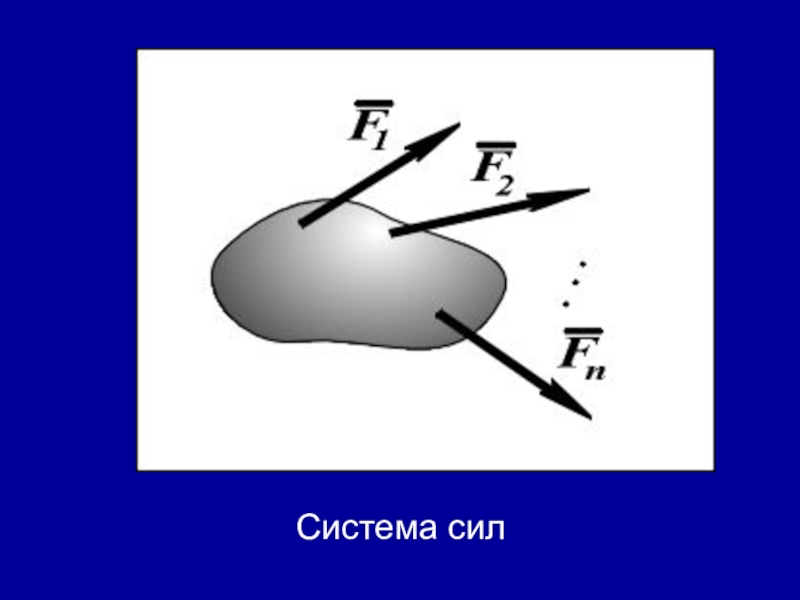
- 7. Система сил
- 8. Уравновешенная система сил
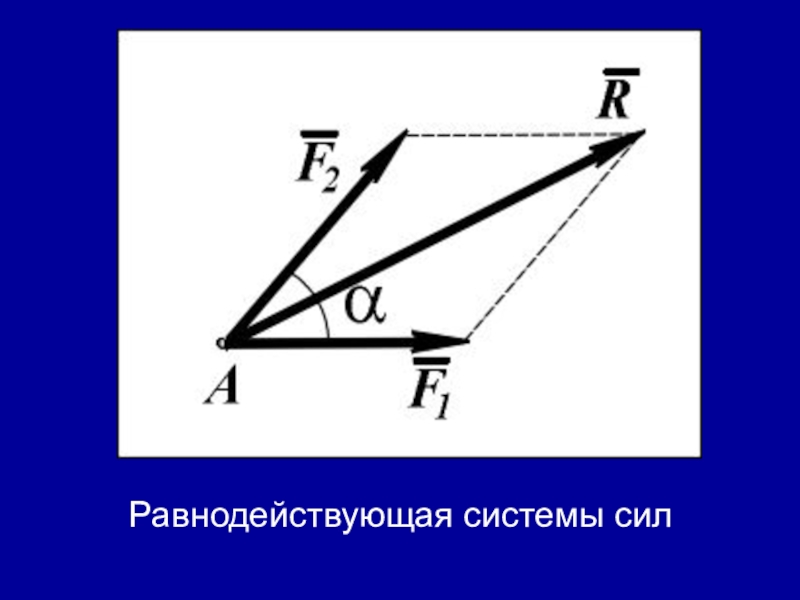
- 9. Равнодействующая системы сил
- 10. 1.3. Аксиомы статикиВ результате обобщения человеческого опыта
- 11. 1.3.1. Первая аксиомаПод действием уравновешенной системы сил
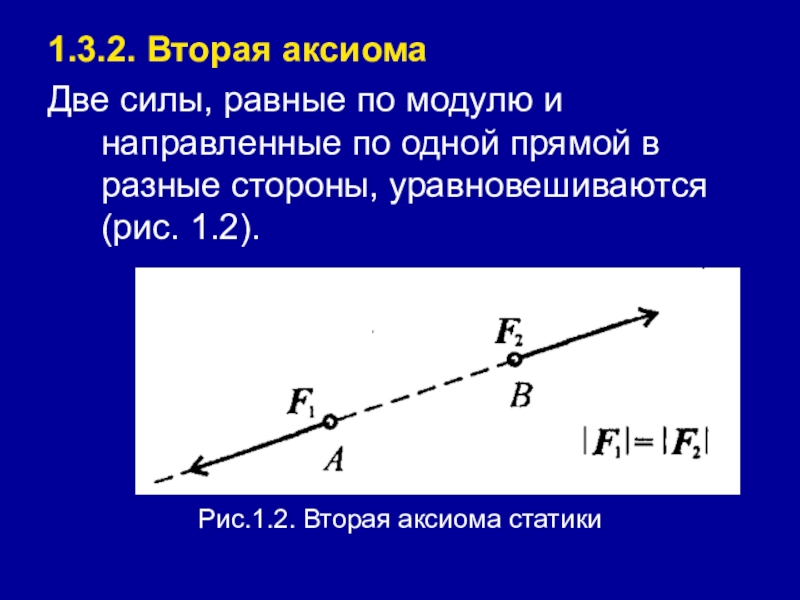
- 12. 1.3.2. Вторая аксиомаДве силы, равные по модулю
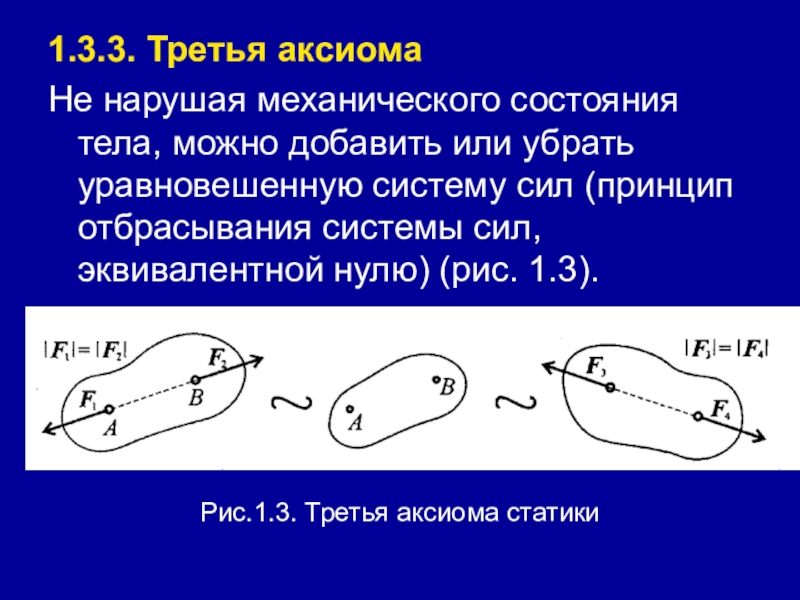
- 13. 1.3.3. Третья аксиомаНе нарушая механического состояния тела,
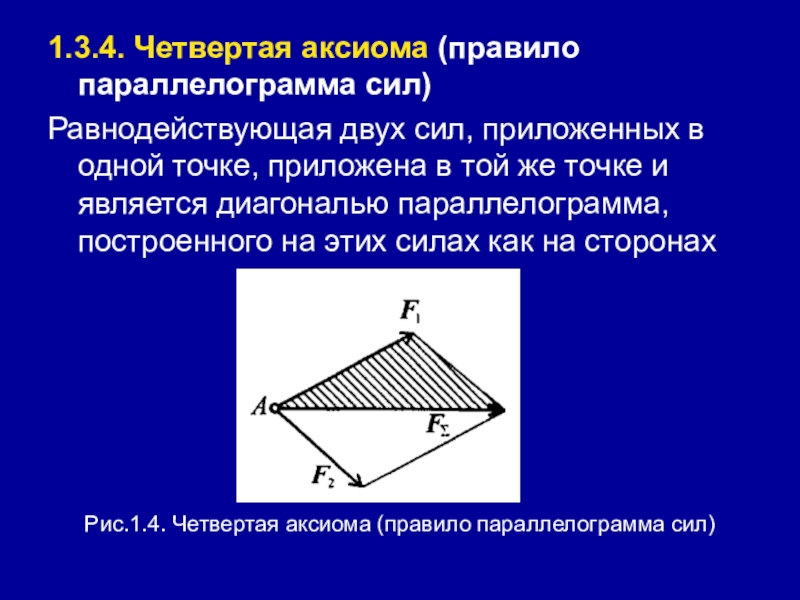
- 14. 1.3.4. Четвертая аксиома (правило параллелограмма сил)Равнодействующая двух
- 15. Вместо параллелограмма можно построить треугольник или многоугольник
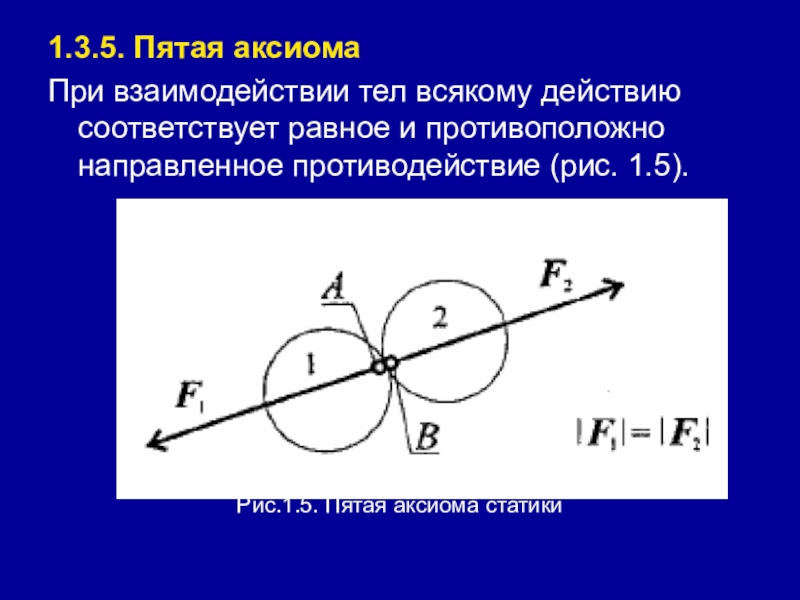
- 16. 1.3.5. Пятая аксиомаПри взаимодействии тел всякому действию
- 17. Силы действующие и противодействующие всегда приложены к
- 18. Следствие из второй и третьей аксиомСилу, действующую
- 19. Сила F приложена в точке А. Требуется
- 20. 1.4. Связи и реакции связейВсе законы и
- 21. Teла, ограничивающие перемещение других тел - называют
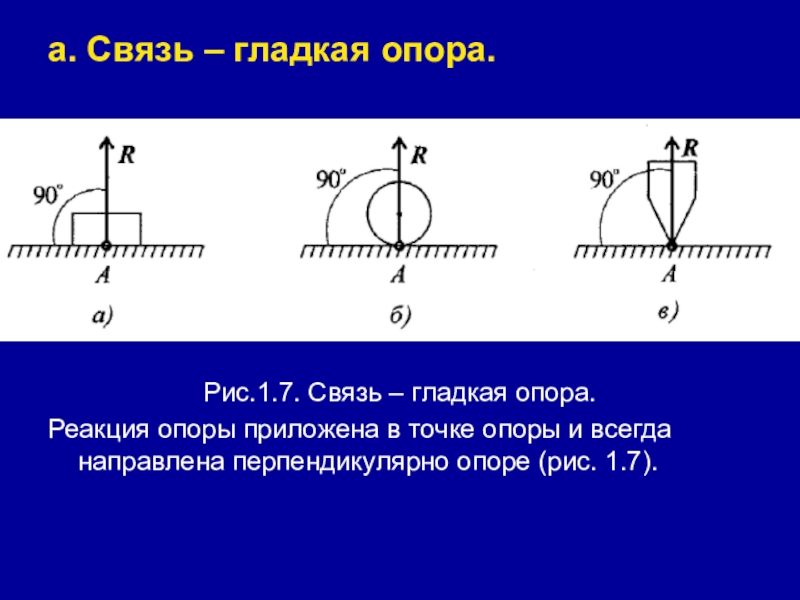
- 22. а. Связь – гладкая опора.Рис.1.7. Связь –
- 23. б. Гибкая связь (нить, веревка, трос, цепь)Груз
- 24. в. Жесткий стержень На схемах стержни изображают
- 25. Возможным перемещением точки называется такое бесконечно малое
- 26. г. Шарнирная опораШарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.1. Подвижный шарнир.Рис.1.10. Подвижный шарнир.
- 27. Стержень, закрепленный на шарнире, может поворачиваться вокруг
- 28. 2. Неподвижный шарнирТочка крепления перемещаться не может.
- 29. д. Защемление или «заделка»Любые перемещения точки крепления
- 30. Реактивную силу принято представлять в виде двух
- 31. Примеры решения задачПример 1. Груз подвешен на
- 32. Решение1. Реакции стержней направлены вдоль стержней, реакции
- 33. 3. Убираем стержень 1, точка А поднимается
- 34. Пример 2. Шар подвешен на нити и
1.1. Задачи теоретической механикиТеоретическая механика — наука о механическом движении материальных твердых тел и их взаимодействии. Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Слайд 21.1. Задачи теоретической механики
Теоретическая механика — наука о механическом движении материальных
твердых тел и их взаимодействии.
Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Слайд 31.2. Понятие о силе и системе сил
Сила — это мера механического
взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т.е. сила есть величина векторная, характеризующаяся точкой приложения (А), направлением (линией действия), величиной (модулем) (рис. 1.1).
Силу измеряют в ньютонах,
1Н= 1кг • м/с2.
Силу измеряют в ньютонах,
1Н= 1кг • м/с2.
Слайд 5Силы, действующие на тело (или систему тел), делятся на внешние и
внутренние.
Внешние силы бывают активные и реактивные.
Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Внешние силы бывают активные и реактивные.
Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Слайд 6Совокупность сил, действующих на какое-либо тело, называют системой сил.
Эквивалентная система сил
— система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Слайд 101.3. Аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности
механического движения, выраженные в виде законов и теорем.
Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики.
Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики.
Слайд 111.3.1. Первая аксиома
Под действием уравновешенной системы сил абсолютно твердое тело или
материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Слайд 121.3.2. Вторая аксиома
Две силы, равные по модулю и направленные по одной
прямой в разные стороны, уравновешиваются (рис. 1.2).
Рис.1.2. Вторая аксиома статики
Рис.1.2. Вторая аксиома статики
Слайд 131.3.3. Третья аксиома
Не нарушая механического состояния тела, можно добавить или убрать
уравновешенную систему сил (принцип отбрасывания системы сил, эквивалентной нулю) (рис. 1.3).
Рис.1.3. Третья аксиома статики
Рис.1.3. Третья аксиома статики
Слайд 141.3.4. Четвертая аксиома (правило параллелограмма сил)
Равнодействующая двух сил, приложенных в одной
точке, приложена в той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах
Рис.1.4. Четвертая аксиома (правило параллелограмма сил)
Рис.1.4. Четвертая аксиома (правило параллелограмма сил)
Слайд 15Вместо параллелограмма можно построить треугольник или многоугольник сил: силы вычерчивают одну
за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом последней.
Слайд 161.3.5. Пятая аксиома
При взаимодействии тел всякому действию соответствует равное и противоположно
направленное противодействие (рис. 1.5).
Рис.1.5. Пятая аксиома статики
Рис.1.5. Пятая аксиома статики
Слайд 17Силы действующие и противодействующие всегда приложены к разным телам, поэтому они
не уравновешиваются.
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.
Слайд 18Следствие из второй и третьей аксиом
Силу, действующую на твердое тело» можно
перемешать вдоль линии ее
Рис.1.6. Следствие из второй и третьей аксиом
Рис.1.6. Следствие из второй и третьей аксиом
Слайд 19Сила F приложена в точке А. Требуется перенести ее в точку
В.
Используя третью аксиому, добавим в точке В уравновешенную систему сил (F’, F”). Образуется уравновешенная по второй аксиоме система сил [F; F"), Убираем ее и получим в точке В силу F" равную заданной F.
Используя третью аксиому, добавим в точке В уравновешенную систему сил (F’, F”). Образуется уравновешенная по второй аксиоме система сил [F; F"), Убираем ее и получим в точке В силу F" равную заданной F.
Слайд 201.4. Связи и реакции связей
Все законы и теоремы статики справедливы для
свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободные тела — тела, перемещение которых не ограничено.
Связанные тела — тела, перемещение которых ограничено другими телами.
Все тела делятся на свободные и связанные.
Свободные тела — тела, перемещение которых не ограничено.
Связанные тела — тела, перемещение которых ограничено другими телами.
Слайд 21Teла, ограничивающие перемещение других тел - называют связями.
Силы, действующие от связей
и препятствующие перемещению, называют реакциями связей
Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
Слайд 22а. Связь – гладкая опора.
Рис.1.7. Связь – гладкая опора.
Реакция опоры приложена
в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
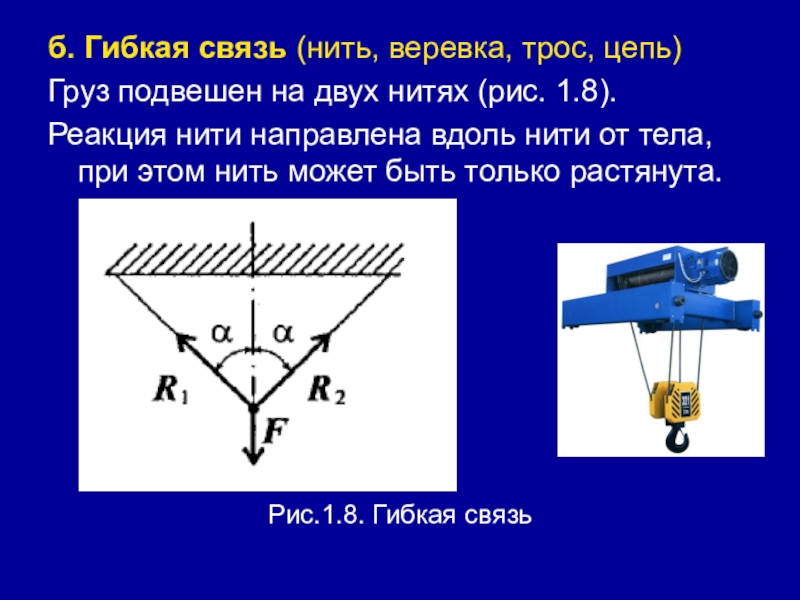
Слайд 23б. Гибкая связь (нить, веревка, трос, цепь)
Груз подвешен на двух нитях
(рис. 1.8).
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Рис.1.8. Гибкая связь
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Рис.1.8. Гибкая связь
Слайд 24в. Жесткий стержень
На схемах стержни изображают толстой сплошной линией (рис.
1.9).
Рис.1.9. Связь – жесткий стержень
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Рис.1.9. Связь – жесткий стержень
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Слайд 25Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается
в данный момент наложенными на него связями.
Убираем стержень 1, в этом случае стержень 2 падает вниз.
Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2.
В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене
Убираем стержень 1, в этом случае стержень 2 падает вниз.
Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2.
В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене
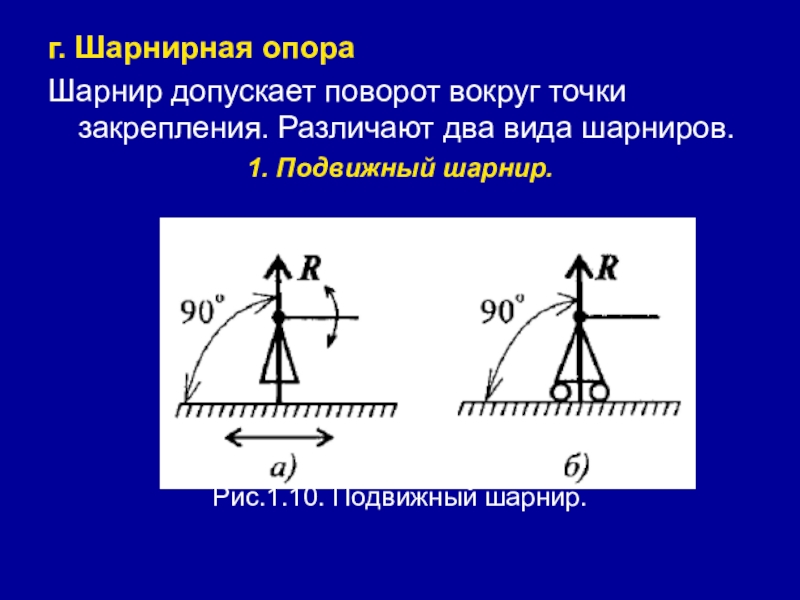
Слайд 26г. Шарнирная опора
Шарнир допускает поворот вокруг точки закрепления. Различают два вида
шарниров.
1. Подвижный шарнир.
Рис.1.10. Подвижный шарнир.
1. Подвижный шарнир.
Рис.1.10. Подвижный шарнир.
Слайд 27Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления
может перемещаться вдоль направляющей (площадки) (рис. 1.10).
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т.к. не допускается только перемещение поперек опорной поверхности
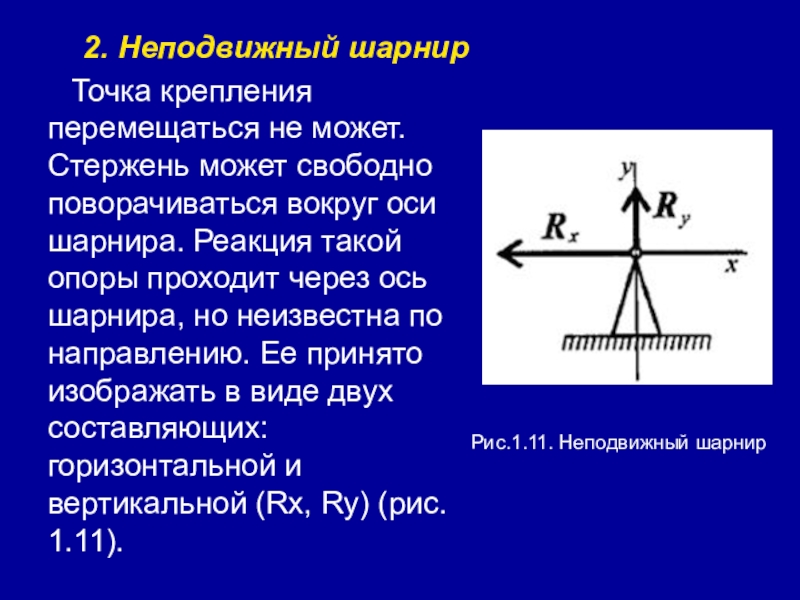
Слайд 282. Неподвижный шарнир
Точка крепления перемещаться не может. Стержень может свободно поворачиваться
вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry) (рис. 1.11).
Рис.1.11. Неподвижный шарнир
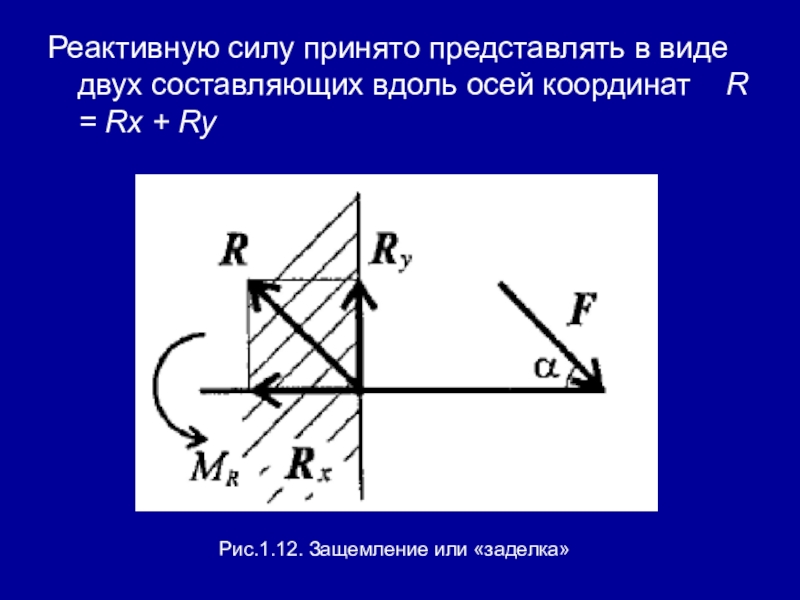
Слайд 29д. Защемление или «заделка»
Любые перемещения точки крепления невозможны.
Под действием внешних сил
в опоре возникают реактивная сила и реактивный момент MR, препятствующий повороту (рис. 1.12).
Рис.1.12. Защемление или «заделка»
Слайд 30Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
R = Rx + Ry
Рис.1.12. Защемление или «заделка»
Слайд 31Примеры решения задач
Пример 1. Груз подвешен на стержнях и канатах и
находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.
Слайд 32Решение
1. Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль
нитей в сторону натяжения (рис. 1.13 а).
2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки А.
Неподвижный блок с действующими на него силами не рассматриваем.
2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки А.
Неподвижный блок с действующими на него силами не рассматриваем.
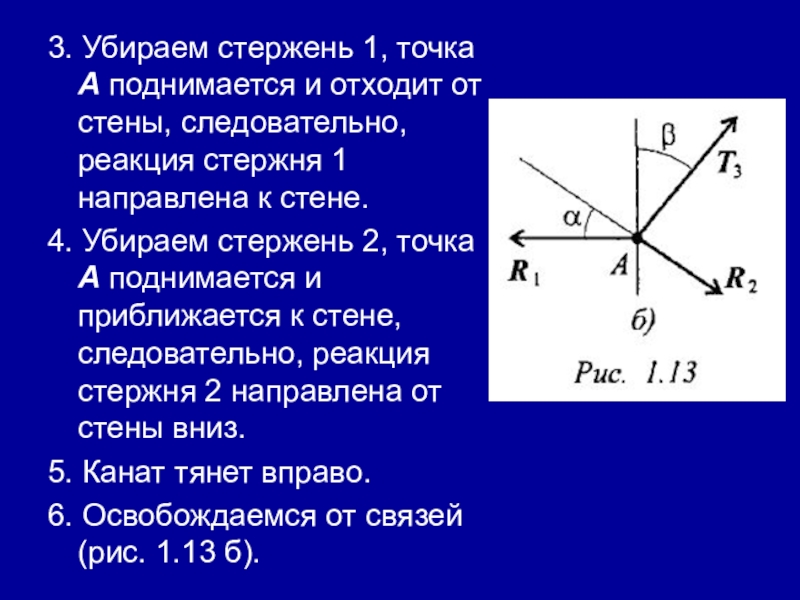
Слайд 333. Убираем стержень 1, точка А поднимается и отходит от стены,
следовательно, реакция стержня 1 направлена к стене.
4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей (рис. 1.13 б).
4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей (рис. 1.13 б).
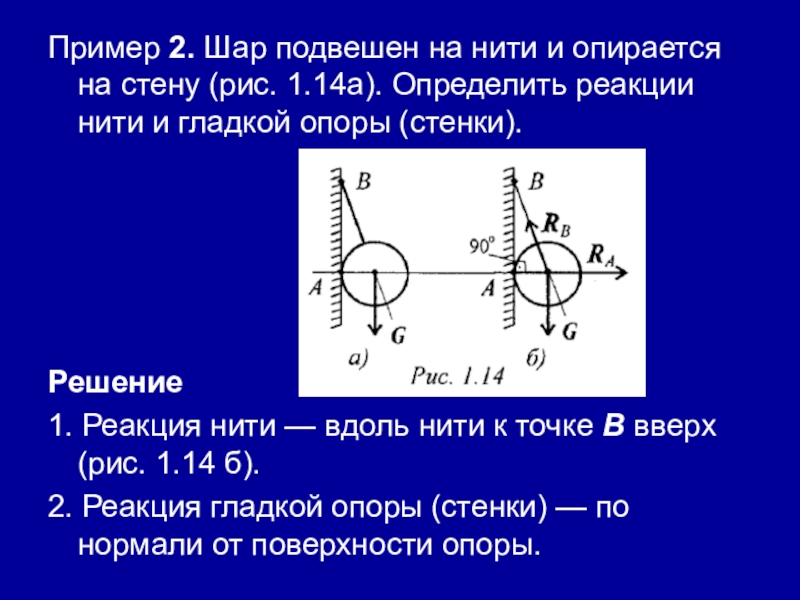
Слайд 34Пример 2. Шар подвешен на нити и опирается на стену (рис.
1.14а). Определить реакции нити и гладкой опоры (стенки).
Решение
1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14 б).
2. Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.
Решение
1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14 б).
2. Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.