Слайд 1Подготовка к ЕГЭ. Решение типовых задач разного уровня.
Подготовила: Бочкова Любовь Ивановна,
учитель физики
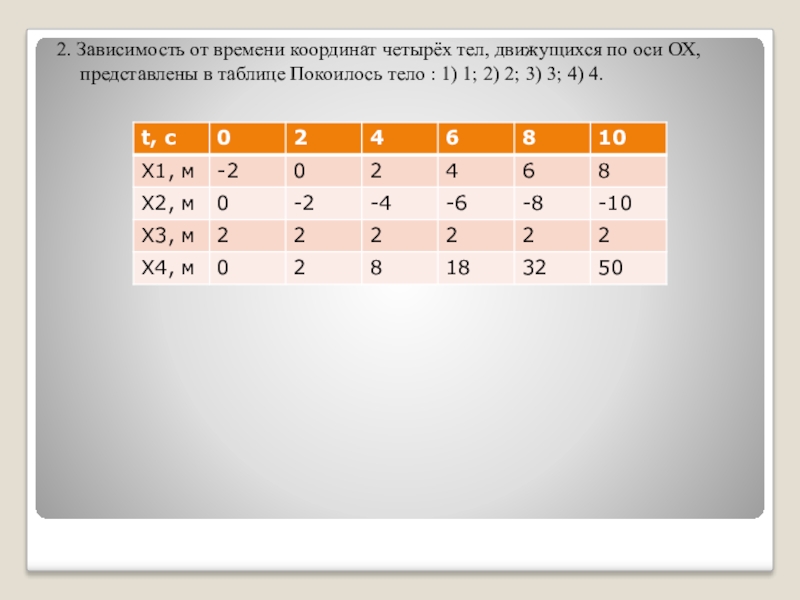
Слайд 32. Зависимость от времени координат четырёх тел, движущихся по оси ОХ,
представлены в таблице Покоилось тело : 1) 1; 2) 2; 3) 3; 4) 4.
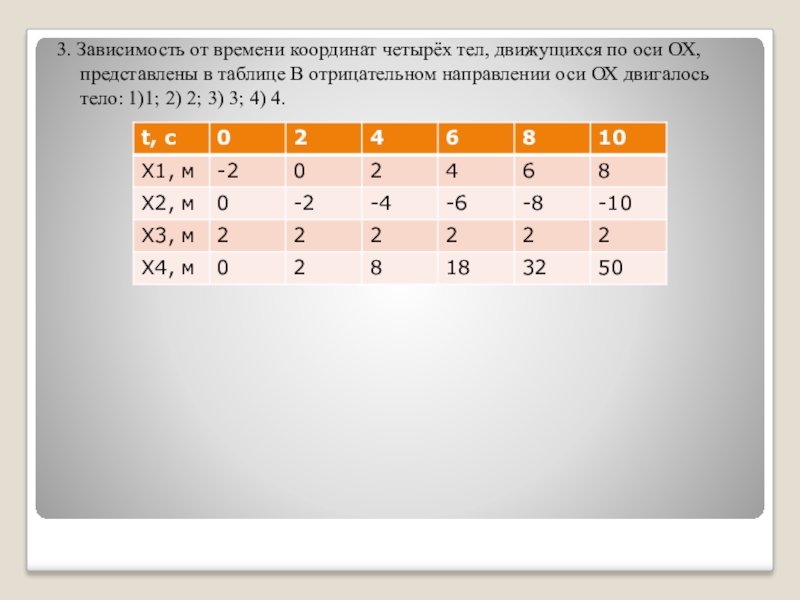
Слайд 43. Зависимость от времени координат четырёх тел, движущихся по оси ОХ,
представлены в таблице В отрицательном направлении оси ОХ двигалось тело: 1)1; 2) 2; 3) 3; 4) 4.
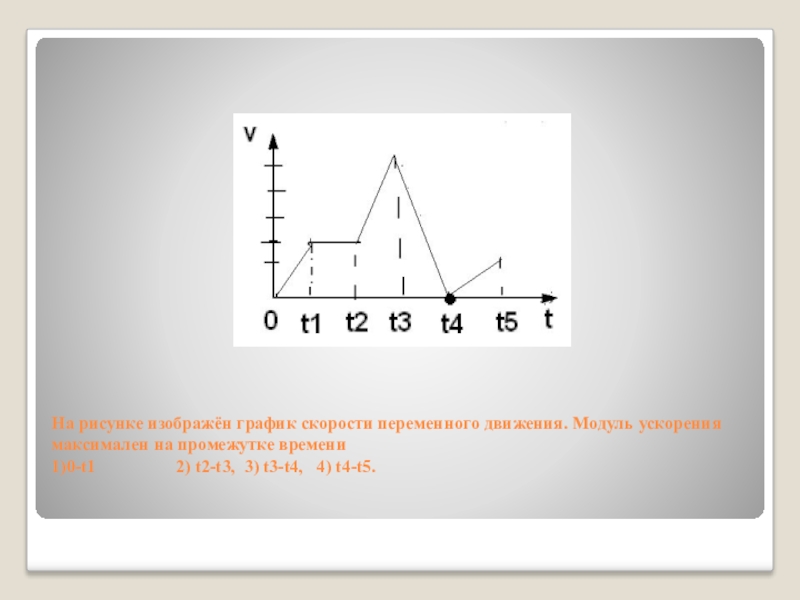
Слайд 5На рисунке изображён график скорости переменного движения. Модуль ускорения максимален на
промежутке времени
1)0-t1 2) t2-t3, 3) t3-t4, 4) t4-t5.
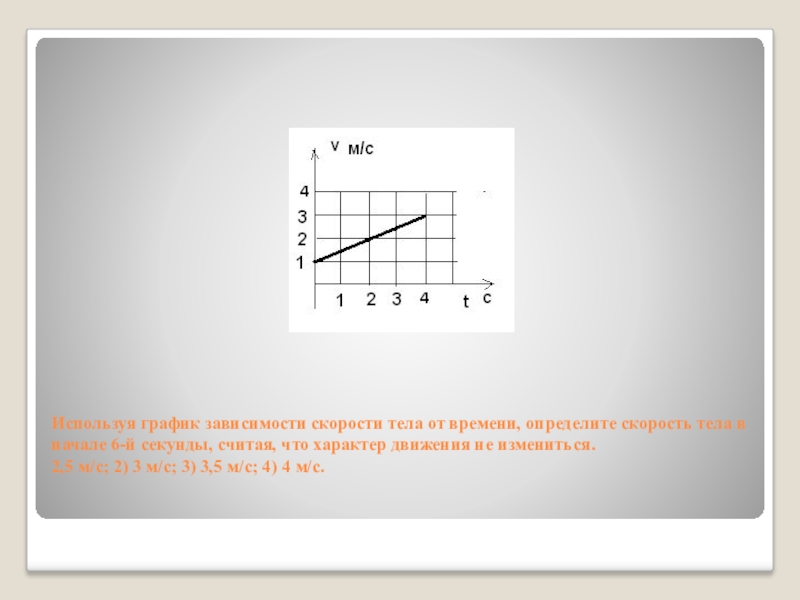
Слайд 6Используя график зависимости скорости тела от времени, определите скорость тела в
начале 6-й секунды, считая, что характер движения не измениться.
2,5 м/с; 2) 3 м/с; 3) 3,5 м/с; 4) 4 м/с.
Слайд 7 Маленький шарик падает вертикально вниз и ударяется о
наклонную плоскость, затем отскакивает от неё в горизонтальном направлении. Импульс шарика перед ударом равен 4 кг м/с импульс шарика после удара 3 кг м/с. Модуль изменения импульса шарика равен: 1) 1 кг м/с; 2) 3,5 кг м/с; 3) 5 кг м/с; 7 кг м/с.
Слайд 8
Маленький шарик падает вертикально вниз и ударяется о
наклонную плоскость, затем
отскакивает от неё в
горизонтальном направлении. Импульс шарика перед ударом
равен 4 кг м/с импульс шарика после удара 3 кг м/с. Модуль
изменения импульса шарика равен:
1) 1 кг м/с; 2) 3,5 кг м/с; 3) 5 кг м/с; 7 кг м/с.
Дано Решение
v1=4 кг м/с Обозначим начальный импульс р1, конечный – р2.
v2=3 кг м/с Изменение импульса Δ p находится как разность между
Δ p-? конечным и начальным импульсами.
Слайд 9 Две тележки массами 20 кг и 30 кг движутся навстречу
друг другу, первая со скоростью 1 м/с, вторая – со скоростью 1, 5 м/с. Модуль импульса системы этих тел после абсолютно неупругого удара равен
0; 2) 25 кг м/с; 3) 62,5 кг м/с; 4) 65 кг м/с.
Слайд 10
Две тележки массами 20 кг и 30 кг движутся навстречу друг
другу, первая со скоростью 1 м/с, вторая – со скоростью 1, 5 м/с. Модуль импульса системы этих тел после абсолютно неупругого удара равен
0; 2) 25 кг м/с; 3) 62,5 кг м/с; 4) 65 кг м/с.
Дано Решение
m1=20 кг По закону сохранения импульса для замкнутых систем тел векторная
m2-30 кг сумма импульсов не изменяется, р10х+р20х=р1х+р2х
v1=1 м/с 20х1-30х1,5=-25 кг м/с
v2=1,5 м/с Ответ: 2.
p-?
Слайд 11
На рисунке приведен график зависимости скорости велосипедиста от времени. Путь, пройденный
велосипедистом за 20 с, равен
1) 125 м 2) 200 м, 3) 225 м, 4) 300 м
Слайд 12На рисунке приведен график зависимости скорости велосипедиста от времени. Путь, пройденный
велосипедистом за 20 с, равен
1) 125 м 2) 200 м, 3) 225 м, 4) 300 м
Решение:
Путь, пройденный телом, численно равен площади фигуры, образующейся под графиком зависимости скорости от времени
S=1/2х(5х10)+10х20=225 м
Ответ: 3.
Слайд 13На рисунке представлены вектор скорости и вектор равнодействующих всех сил, действующих
на тело. Какой из четырех векторов на рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчёта?
1 2) 2 3) 3 4) 4
Слайд 14На рисунке представлены вектор скорости и вектор равнодействующих всех сил, действующих
на тело. Какой из четырех векторов на рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчёта?
1 2) 2 3) 3 4) 4
Решение
По второму закону Ньютона
F=ma. Следовательно сила
сонаправлена с ускорением.
Ответ:2.
Слайд 15На тележке , двигающейся с постоянным ускорением 0,5 м/с2, покоится брусок.
Со стороны тележки на брусок действует сила трения 1,5 Н. Сила трения, действующая со стороны бруска на тележку равна
1) 0 Н 2) 0,5 Н 3), 1,5 Н 4) 3 Н.
Слайд 16
Два тела движутся со скоростями 4 м/с и 3 м/с, по
взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1) 1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.
Слайд 17Два тела движутся со скоростями 4 м/с и 3 м/с, по
взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.
Дано Решение
V1=4 м/с
V2= 3 м/с
V12-?
Слайд 18Два тела движутся со скоростями 4 м/с и 3 м/с, по
взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.
Дано Решение
V1=4 м/с
V2= 3 м/с
V12-?
V12=5 м/с
Ответ: 5 м/с.
Слайд 19Тело движется по прямой. Под действием постоянной силы величиной 4 Н
за 2 с импульс тела увеличился и стал равен 20 кг м/с. Первоначальный импульс тела равен
1) 4 кг м/с, 2) 8 кг м/с, 3) 12 кг м/с, 4) 28 кг м/с
Слайд 20Тело движется по прямой. Под действием постоянной силы величиной 4 Н
за 2 с импульс тела увеличился и стал равен 20 кг м/с. Первоначальный импульс тела равен
4 кг м/с, 2) 8 кг м/с, 3) 12 кг м/с, 4) 28 кг м/с.
Дано Решение
F=4 Н по второму закону Ньютона
t=2c F=ma=m(v-v0)/t=(mv-mv0)/t=
p2=20 кг м/с = (p2-p1)/t, p1=p2-Ft, p1=20-4x2=
р1-? =12 кг м/с
Ответ: 3.
Слайд 21На рисунке схематически изображена лестница АС, прислоненная к стене. Каков модуль
момента силы тяжести F, действующей на лестницу относительно точки С?
1) Fx OC, 2) FxOD, 3) FxAC, 4) FxDC
Слайд 22На рисунке схематически изображена лестница АС, прислоненная к стене. Каков модуль
силы тяжести F, действующей на лестницу относительно точки С?
1) Fx OC, 2) FxOD, 3) FxAC, 4) FxDC
Решение
По определению, модуль момента силы относительно оси равен произведению модуля силы на плечо (длину перпендикуляра, соединяющего ось с линией действия силы). Как видно из рисунка в условии задачи, модуль момента силы равен M=FxDC.
Ответ:4.
Слайд 23
Задача.
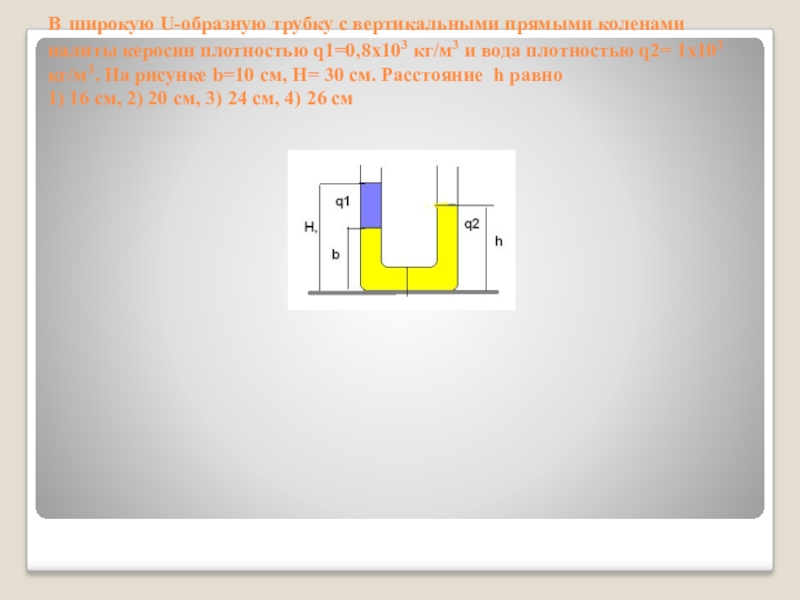
В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью
q1=0,8x103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см
Слайд 24В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью
q1=0,8x103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.
Дано Решение
q1=0,8x103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости .
b=0,10 м
H= 0,30 м
h -?
Слайд 25В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью
q1=0,8x103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.
Дано Решение
q1=0,8x103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости . В левом колене налиты
b=0,10 м две жидкости, поэтому р1 = q1g(H-b)+ q2 gb.
H= 0,30 м
h -?
Слайд 26В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью
q1=0,8x103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.
Дано Решение
q1=0,8x103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости . В левом колене налиты
b=0,10 м две жидкости, поэтому р1 = q1g(H-b)+ q2 gb.
H= 0,30 м В правом колене р2=q2 gh. р1 =р2,
h -? q1g(H-b)+ q2 gb= q2 gh, h=q1/ q2 (H-b)+ b
h=0,8(0,3-0,1)+0,1= 0,26=26 см.
Ответ: 4.
Слайд 27Математический маятник совершает малые колебания. В таблице представлены координаты маятника для
различных промежутков времени. Длина нити маятника приблизительно равна
1) 30 см, 2) 45 см, 3) 50 см, 4) 65 см
Слайд 28
Математический маятник совершает малые колебания. В таблице представлены координаты маятника для
различных промежутков времени. Длина нити маятника приблизительно равна
1) 30 см, 2) 45 см, 3) 50 см, 4) 65 см
Дано Решение
π =3,14 Воспользуемся формулой периода T=2π .
g=9,8 м/с2 По определению периода Т=1,6 с.
L-? L= , L=0,65 м
Ответ: 4.
Слайд 29Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания.
Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? Для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
Слайд 30Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания.
Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
Слайд 31Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания.
Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
Слайд 32Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания.
Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
Слайд 33
Задача.
Груз массой 100 кг удерживается на месте с помощью рычага,
приложив вертикальную силу 350 Н. Рычаг состоит из шарнира без трения и однородного массивного стержня длиной 5 м.
Расстояние от оси шарнира до точки подвеса груза равно 1 м.
Масса стержня равна
1) 25 кг, 2) 35 кг, 3) 20 кг, 4) 30 кг
Слайд 34
Задача.
Груз массой 100 кг удерживается на месте с помощью рычага,
приложив
вертикальную силу 350 Н. Рычаг состоит из шарнира
без трения и однородного массивного стержня длиной 5 м.
Расстояние от оси шарнира до точки подвеса груза равно 1 м.
Масса стержня равна
1) 25 кг, 2) 35 кг, 3) 20 кг, 4) 30 кг
Дано Решение
L=5 м FL-Mgb-mgL/2=0
F=350H m=2(FL-Mgb)/gL=2(F/g-Mb/L)=2(350/10-100х1/5)=30 кг
M=100 кг
G=9,8 Н/кг Ответ: 4.
b= 1 м
m-?
Слайд 35
Задача.
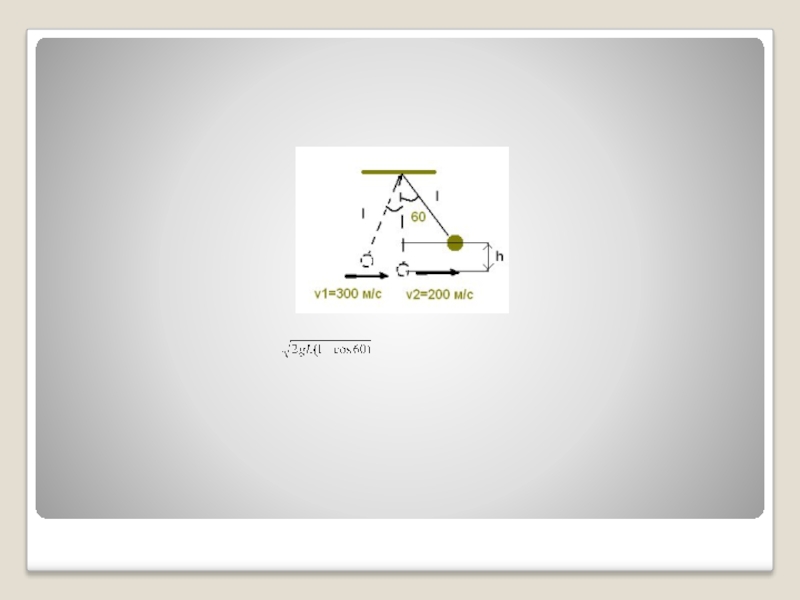
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят
от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Слайд 36
Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см,
отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с.
L= 0,9 м
α=60
β-?
Слайд 37
Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят
от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2..
L= 0,9 м
α=60,
β-?
.
Слайд 38
Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят
от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп.=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2.
L= 0,9 м h=L-Lcos60=L(1-cos60), 2gL(1-cos60)=u2.
α=60
β-?
Слайд 39
Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят
от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп.=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2. Определим неизвестную высоту.
L= 0,9 м h=L-Lcos60=L(1-cos60), 2gL(1-cos60)=u2.
α=60 После столкновения с пулей Mu12/2=Mgh1, u12 =2gh1,
β-? h1=L(1-cos β ) , u12 =2g L(1-cos β ) , cos β =1- u12 /2gL=
=1 – 1/2gL( +m/M(v1-v))2=7/9.
Ответ: arccos(7/9)
Слайд 40
Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой
амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .
Слайд 41
Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой амплитудой.
Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .
Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3
g=9,8 м/с2
T-?
Слайд 42
Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой
амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .
Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3 Найдём эту силу.
g=9,8 м/с2 В данной задаче этой силой является
T-? выталкивающая сила F=qgV=qgSx.
Слайд 43
Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой
амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .
Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3 Найдём эту силу.
g=9,8 м/с2 В данной задаче этой силой является
T-? выталкивающая сила F=qgV=qgSx.
На ареометр, смещенный от положения равновесия на расстояние х, действует возвращающая сила F=-qgSx (2)
где – qgSкоэффициент возвращающей силы.
Из уравнения (1) и (2) получаем: T=2/r, =2/0,002
Ответ: 4 с.
Слайд 44
Задача.
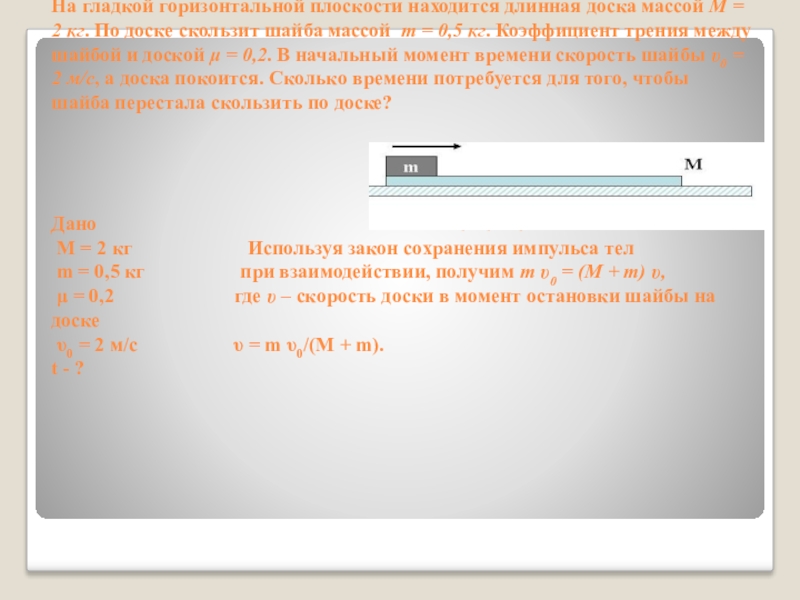
На гладкой горизонтальной плоскости находится длинная доска массой М = 2
кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
Слайд 45
Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М = 2
кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m).
t - ?
Слайд 46
Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М = 2
кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m). Эту скорость доска приобрела
t - ? за время движения шайбы по доске υ = at под действием
силы трения шайбы о доску.
Слайд 47
Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М =
2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m). Эту скорость доска приобрела
t - ? за время движения шайбы по доске υ = at под действием
силы трения шайбы о доску. Сила трения, действующая на
шайбу, равна по модулю силе трения, действующей на доску
F= μ mg, следовательно, a =F /M = μ mg/M.
t = υ/a = M m υ0 / (M + m) μ mg = 0, 8 с.
Ответ: 0,8 с.
Слайд 48
С высоты Н над землёй из состояния покоя начинает свободно падать
стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Задача.
Слайд 49
С высоты Н над землёй из состояния покоя начинает свободно падать
стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м
V0=0
α=300
H-?
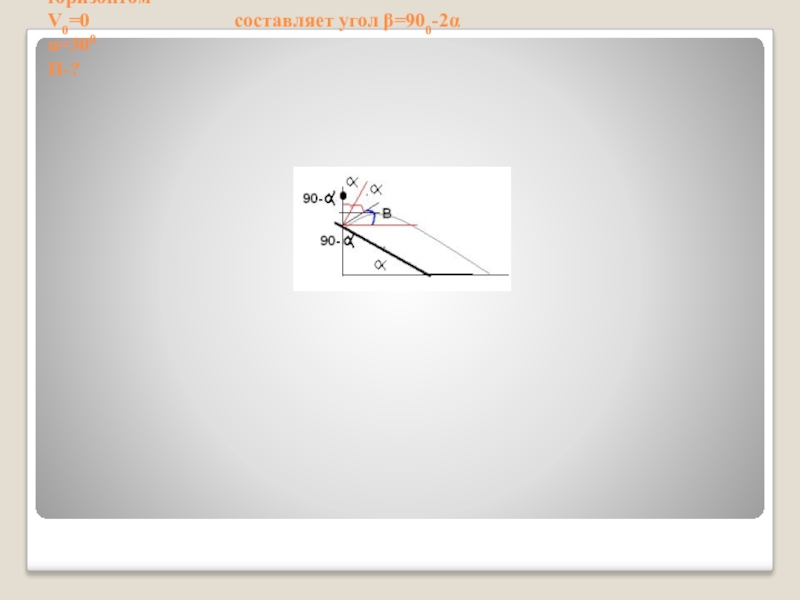
Слайд 50
С высоты Н над землёй из состояния покоя начинает свободно падать
стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300
H-?
Слайд 51
С высоты Н над землёй из состояния покоя начинает свободно падать
стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300 3)Vx=V10cos β =gtcos β =gtsin2α
H-? V10 –скорость перед ударом
Слайд 52
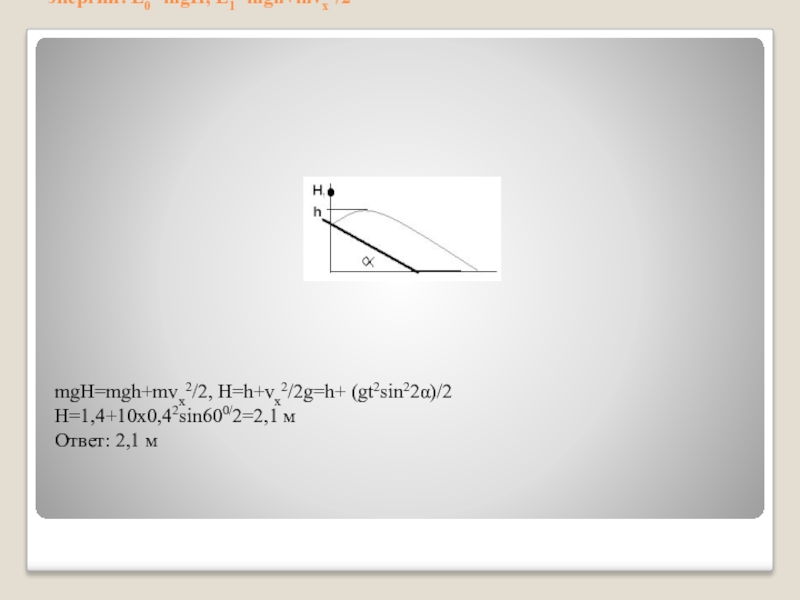
С высоты Н над землёй из состояния покоя начинает свободно падать
стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300
g=9,8 м/с2 3)Vx=V10cos β =gtcos β =gtsin2α
H-? V10 –скорость перед ударом
4) Применим закон сохранения
энергии: Е0=mgH, E1=mgh+mvx2/2
mgH=mgh+mvx2/2, H=h+vx2/2g=h+ (gt2sin22α)/2
H=1,4+10х0,42sin600/2=2,1 м
Ответ: 2,1 м
Слайд 53
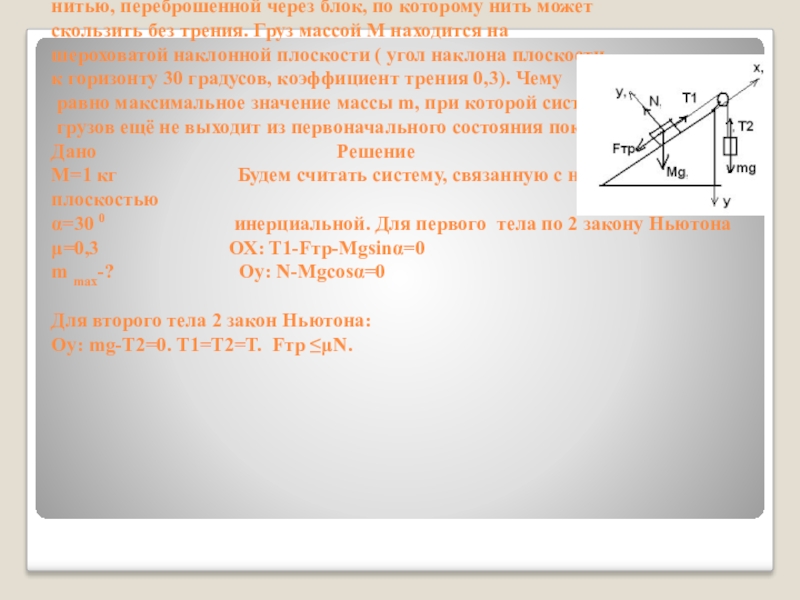
Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой нитью,
переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3. Чему
равно максимальное значение массы m, при которой система грузов ещё не выходит из первоначального состояния покоя?
Слайд 54
Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью,
переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0
Слайд 55
Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью,
переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0
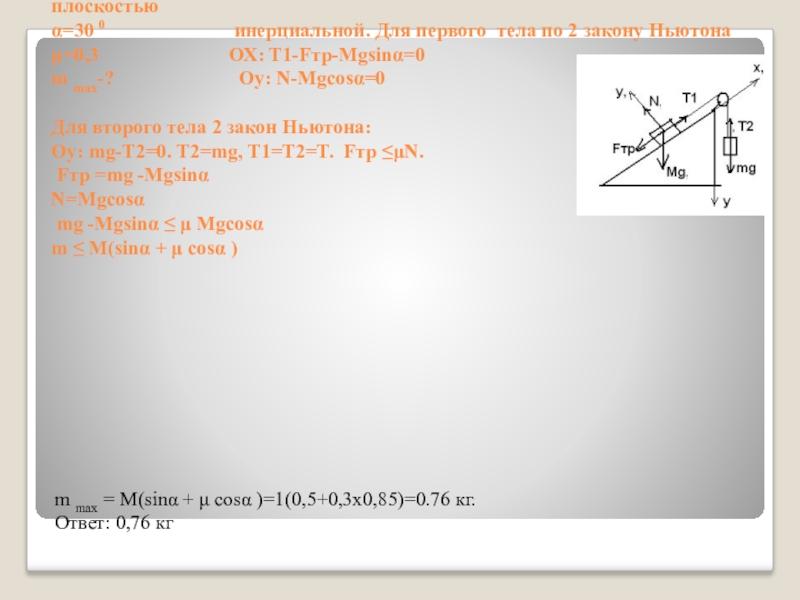
Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т1=Т2=Т. Fтр ≤μN.
Слайд 56
Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью,
переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0
Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т2=mg, Т1=Т2=Т. Fтр ≤μN.
Слайд 57
Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью,
переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0
Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т2=mg, Т1=Т2=Т. Fтр ≤μN.
Fтр =mg -Mgsinα
N=Mgcosα
mg -Mgsinα ≤ μ Mgcosα
m ≤ M(sinα + μ cosα )
m max = M(sinα + μ cosα )=1(0,5+0,3х0,85)=0.76 кг.
Ответ: 0,76 кг
Слайд 58
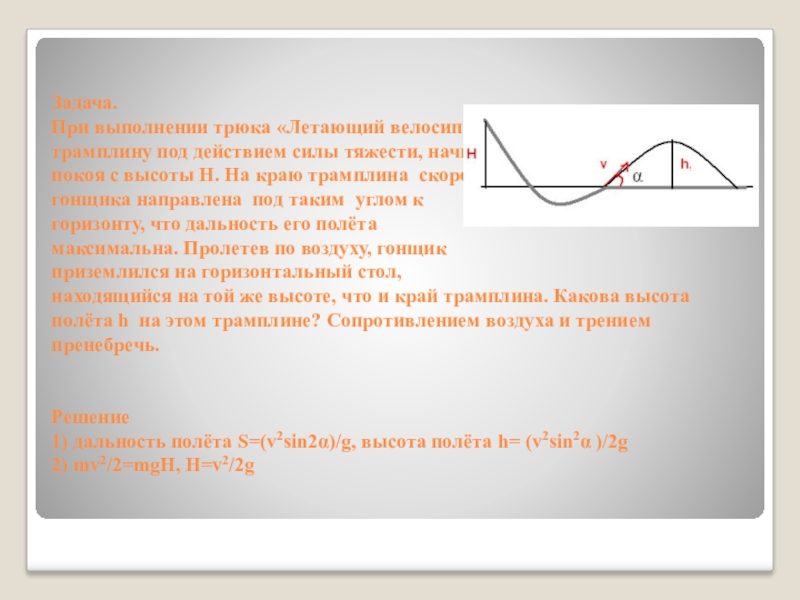
Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием
силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Слайд 59
Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием
силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
Слайд 60
Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием
силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
2) mv2/2=mgH, H=v2/2g
Слайд 61
Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием
силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
2) mv2/2=mgH, H=v2/2g
3) S максимально, если v2sin2α максимально, т.е. sin2α =1, α =45 0.
h= H sin2α =Hsin45 0=H/2.
Ответ: H/2
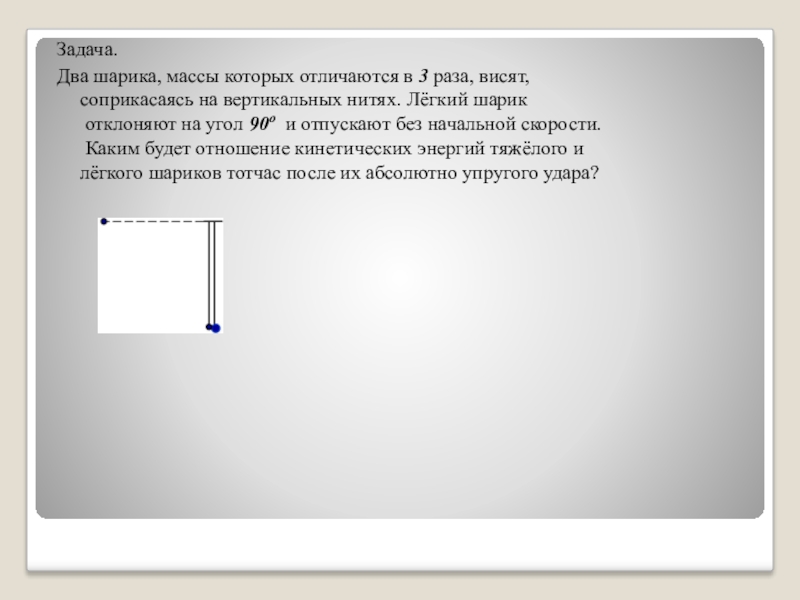
Слайд 62Задача.
Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь
на вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?
Слайд 63
Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь на
вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?
Решение.
До удара энергией будет обладать только лёгкий шарик, сначала потенциальной Ep = mgh , (где h = длине нити, т. к. угол прямой) а затем кинетической Ek = mυ2/2.
Слайд 64
Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь на
вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?
Решение.
До удара энергией будет обладать только лёгкий шарик, сначала потенциальной Ep = mgh , (где h = длине нити, т. к. угол прямой) а затем кинетической Ek = mυ2/2. Т. к. в системе действуют только потенциальные силы, и удар абсолютно упругий, то можно применить и закон сохранения импульса и закон сохранения механической энергии: mυ = mυ1 + 3mυ2, υ2 =( υ - υ1 ) / 3. mυ2 = mυ1 2 + 3mυ22, υ22 = (υ2 - υ1 2) / 3, (υ2 - υ1 2) / 3 =( υ - υ1 )2 / 32, (υ + υ1 ) = (υ - υ1 ) / 3, υ1 = - υ/2. υ2 =( υ+ υ/2 ) / 3 = υ/2.
Для тяжёлого шарика E1 = 3mυ2 /8, для лёгкого E2 = mυ2 /8. E1/ E2 = 3.
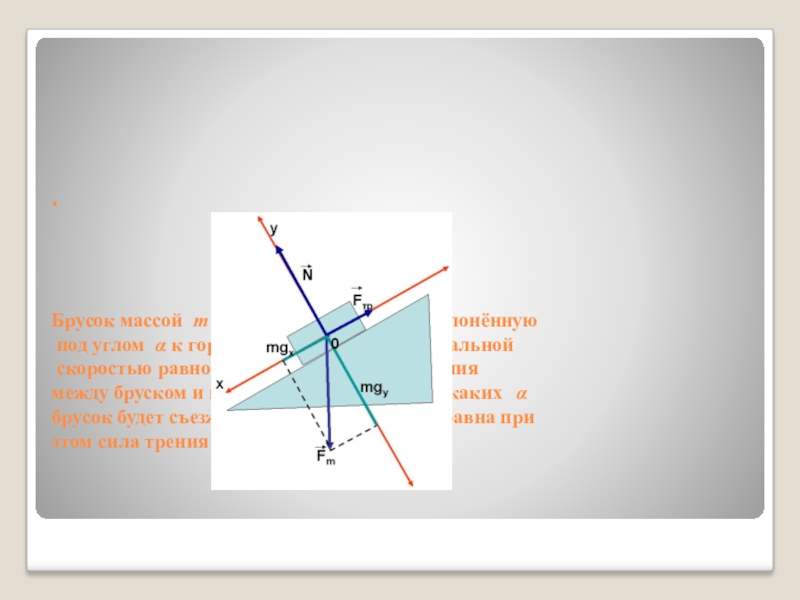
Слайд 65.
Брусок массой m кладут на плоскость, наклонённую
под углом α
к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна при
этом сила трения бруска о плоскость?
Слайд 66.
Брусок массой m кладут на плоскость, наклонённую
под углом α
к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна
при этом сила трения бруска о плоскость?
Решение.
Запишем второй закон Ньютона в векторной форме
ma=N+Fтр+Fтяж . Выберем оси координат и запишем
это уравнение в проекциях на оси
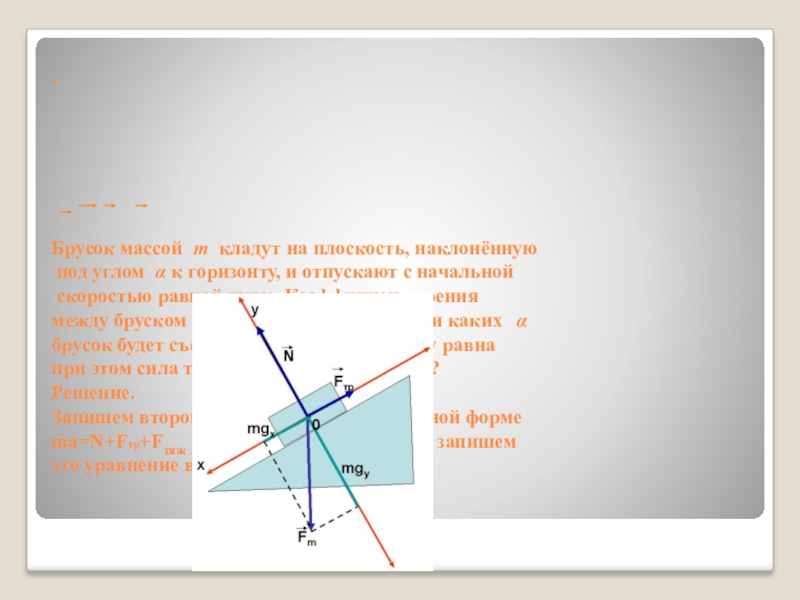
Слайд 67.
Брусок массой m кладут на плоскость, наклонённую
под углом α
к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна
при этом сила трения бруска о плоскость?
Решение.
Запишем второй закон Ньютона в векторной форме
ma=N+Fтр+Fтяж . Выберем оси координат и запишем
это уравнение в проекциях на оси
ОХ: maх=-Fтр+Fтяж sin α
ОУ: maу=N-Fтяж cos α
При равномерном скольжении a=0,
Fтр = mgsin α , mgcos α = N,
Fтр = μN = μ mgcos α. mgsin α= μ mgcos α, μ= sinα / cos α = tg α.
α = arctg μ.
Брусок начнёт съезжать с наклонной плоскости при условии α > arctg μ.
Сила трения равна Fтр = μ mgcos α.