- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Молекулалық-кинетикалық теория негiздерi
Содержание
- 1. Презентация по физике на тему Молекулалық-кинетикалық теория негiздерi
- 2. Сабақ тақырыбы: Молекулалық-кинетикалық теорияның негiзгi ұғымдарыМақсаты:
- 3. Сабақтың құрылымы:Сабақты ұйымдастыру кезеңі.Үй тапсырмасын сұрау.Жаңа сабақты түсіндіру. Бекіту.Қорытынды.Білімдерін бағалау.Үйге тапсырма.
- 4. ЖОСПАР:Молекулалық-кинетикалық теорияның негiзгi ұғымдарыМолекуллар массасы мен өлшемi.
- 5. § 1.1 Молекулалық-кинетикалық теорияның негiзгi ұғымдарыДене құрылымының
- 6. § 1.2 Молекуллар массасы мен өлшемi. Салыстырмалы
- 7. Молекуланың өлшемiн былайша анықтауға болады. Бiр молекуланың
- 8. § 1.3 Молекулалар арасындағы өзара әсерлесу күштерi.
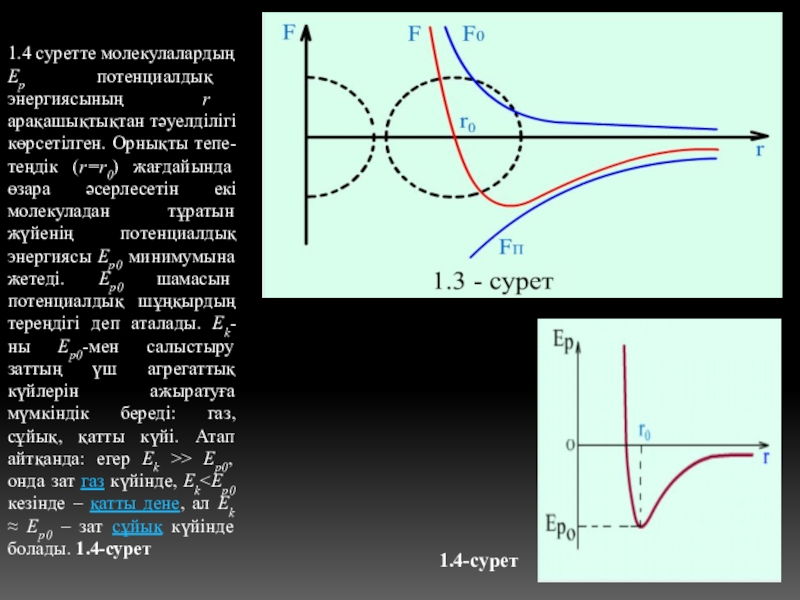
- 9. 1.4 суретте молекулалардың Ep потенциалдық энергиясының r
- 10. § 1.4 Газдың молекулалық-кинетикалық теориясының негiзгi теңдеуiИдеал
- 11. Ендi идеал газдың ыдыс қабырғасына әсер ететiн
- 12. Бұл қатынастың қорытындысы. Газдың барлық молекулаларда vx
- 13. § 1.5 Газдың макропараметрлерi. Tемпература және оны
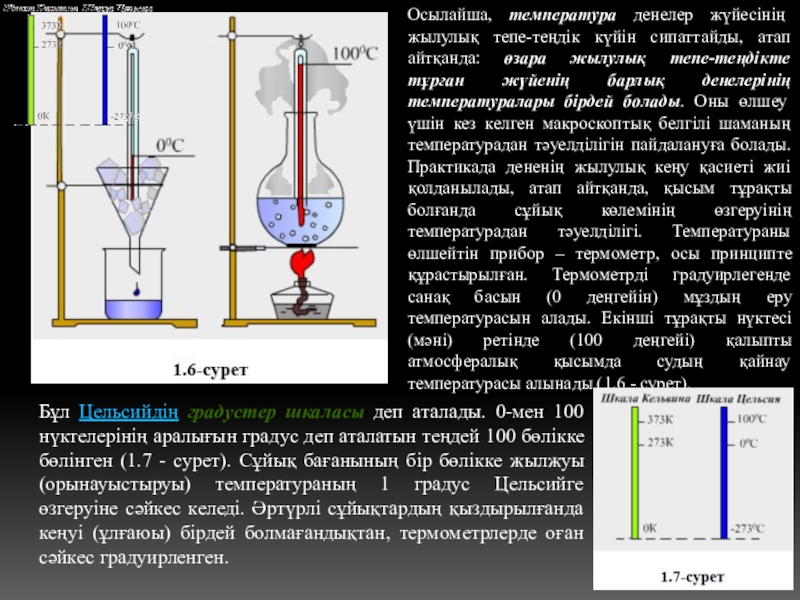
- 14. Осылайша, температура денелер жүйесiнiң жылулық тепе-теңдiк күйiн
- 15. § 1.6 Температура - идеал газ молекуласының
- 16. Температураның абсолюттi нөлi (Т = 0) деп
- 17. Осылайша, абсолюттi температура газ молекулаларының жылулық қозғалысының
- 18. § 1.7 Газ молекуласының жылдамдығы. Штерн тәжiрибесiГаз
- 19. § 1.8 Больцман тұрақтысы. Клайперон-Менделеевтiң күй теңдеуiТемпература
- 20. Молекулалық кинетикалық теорияның негiзгi теңдеуi p қысым,
- 21. § 1.9 Газдағы изопроцесстер және олардың графиктерi.Параметрлерiнiң
- 22. Қысым тұрақты болған кезде термодинамикалық жүйе күйiнiң
- 23. Үйге тапсырма беру. Молекулалық-кинетикалық теория негiздерi тарауы18 – жаттығу № 1,3,4,5
- 24. Зейін қойып тыңдағандарыңызға көп -көп РАХМЕТ!
Слайд 2Сабақ тақырыбы: Молекулалық-кинетикалық теорияның негiзгi ұғымдары
Мақсаты: Білімділік: а) Молекулалық-кинетикалық
ә) д) Молекулалық-кинетикалық теория мысалдар арқылы түсіндіру.
Дамытушылық: Тәжірібесі арқылы оқушылардың ғылыми көзқарасын қалыптастыру.
Тәрбиелік: Тәжірибелер мен мысалдар негізінде пәнге қызығушылыққа тәрбиелеу.
Сабақтың әдісі: Сын тұрғысынан ойлау бағдарламасының стратегияларының элементтерін пайдалану.
Сабақтың түрі: Жаңа сабақты меңгерту сабағы.
Сабақтың көрнекіліктері: Интерактивті тақта, слайд, плакат
Слайд 3Сабақтың құрылымы:
Сабақты ұйымдастыру кезеңі.
Үй тапсырмасын сұрау.
Жаңа сабақты түсіндіру.
Бекіту.
Қорытынды.
Білімдерін бағалау.
Үйге тапсырма.
Слайд 4ЖОСПАР:
Молекулалық-кинетикалық теорияның негiзгi ұғымдары
Молекуллар массасы мен өлшемi. Салыстырмалы молярлық және молекулалық
Молекулалар арасындағы өзара әсерлесу күштерi. Сұйық, газ тәрiздес және қатты денелердiң құрылымы
молекулалық-кинетикалық теориясының негiзгi теңдеуi
Газдың
Газдың макропараметрлерi. Tемпература және оны өлшеу
Температура - идеал газ молекуласының орташа кинетикалық энергиясының өлшемi
Газ молекуласының жылдамдығы. Штерн тәжiрибесi
Больцман тұрақтысы. Клайперон-Менделеевтiң күй теңдеуi
Газдағы изопроцесстер және олардың графиктерi
Слайд 5§ 1.1 Молекулалық-кинетикалық теорияның негiзгi ұғымдары
Дене құрылымының молекулалық кинетикалық теориясы деп
Молекулалық-кинетикалық теория (МКТ) негiзi мынадай үш қасиеттен тұрады:
барлық денелер бөлшектерден – атомдардан, молекулалардан, оң және терiс зарядталған иондардан – тұрады;
бұл бөлшектер барлық уақытта үздiксiз және бейберекет қозғалыста болады;
бөлшектер арасында өзара әсерлесу күштерi – тартылу және тебiлу күштерi бар. Ол күштер электрлiк сипатқа ие. Бөлшектердiң өзара гравитациялық әсерлесуi өте аз.
Бұл тұжырымдардың ақиқаттылығы көптеген физикалық бақылаулар мен тәжiрибелер жүргiзу арқылы дәлелденген. МКТ-ның негiзгi көзқарастарына ең нақты дәлел бола алатын мысалдар:
броундық қозғалыс құбылысы (Броун);
молекулалық диффузия құбылысы;
қазiргi заманғы приборлар көмегiмен алынған жеке атомдар мен молекулалар кескiнi. 1-шi суретте вольфрам инесiнiң ұшында атомдардың орналасуы (ақ дақтар), ал 2-шi суретте кремний пластинасы бетiнiң микрофотографиясы келтiрiлген, мұндағы дөңдер – кремнийдiң жеке атомдары.
1.1-сурет
1.2-сурет
Слайд 6§ 1.2 Молекуллар массасы мен өлшемi. Салыстырмалы молярлық және молекулалық масса.
Әртүрлi денелер молекуласының масса бiрлiгi ретiнде 12С көмiртегi изотобы атомының mocмассасының 1/12 бөлiгi алынады. Ол атомдық масса бiрлiгi (а.м.б.) деп аталады және мынаған тең:
1 а.м.б.=1,66·10-27кг. (1.1)
Заттың салыстырмалы молекулалық массасы МR деп заттың бiр молекула m0 массасының көмiртегi атомы moc массасының 1/12 бөлiгiне қатынасын айтады:
(1.2)
Зат мөлшерi деп берiлген жүйенiң бөлшектерiнiң, құрылымдық элементерiнiң, санына пропорционал ν шаманы айтады. Оны моль арқылы жазу қабылданған. Массасы 0,012 кг 12С көмiртегiнде қанша атом болса, сонша молекуладан (атомнан) тұратын зат мөлшерi бiр моль деп аталады. Бұл сан Авогадро тұрақтысы деп аталады және NA арқылы белгiленедi:
NA ≈ 6·1023 моль-1. (1.3)
Сәйкесiнше, кез келген заттың 1 молiнде атомдар саны мен молекулалар саны бiрдей болады. Егер денедегi зат мөлшерi ν мольден тұрса, онда денедегi молекулалар N саны мынаған тең:
N = ν ·NA. (1.4)
Заттың молярлық массасы М деп бiр моль мөлшерiнде алынған зат массасын айтады. Ол бiр молекула массасының m0 Авогадро санына NA көбейтiндiсiне тең:
М = m0· NA кг/моль. (1.5)
Молярлық және молекулалық массалар арасында мынадай қарапайым байланыс бар:
М = 10-3 ·Мr кг/моль. (1.6)
Кез келген зат мөлшерiнiң m массасы бiр молекуланың массасын денедегi молекулалар санына көбейткенге тең:
m = m0· N кг. (1.7)
(1.5) және (1.7) формулаларын пайдаланып (1.4) өрнегiнен мынаны алу қиын емес:
ν = m / М және N = ν·NA =
NAA ·m / M . (1.8)
Бөлшектердiң массасымен өлшемдерiн қосымша тәжiрибелiк деректердi пайдалана отырып есептеуге болады. Жеке жағдайда, молекулалардың сызықты өлшемдерiн бағалауға болады.
Слайд 7Молекуланың өлшемiн былайша анықтауға болады. Бiр молекуланың алатын V0 көлемi зат
, мұнда ρ=m/V – заттың тығыздығы. Молекуланың формасы радиусы r шар тәрiздес болсын. Сондықтан . Осыдан:
(1.9)
Мысалы, су молекуласының радиусы мына шамаға тең:
Слайд 8§ 1.3 Молекулалар арасындағы өзара әсерлесу күштерi. Сұйық, газ тәрiздес және
Молекулалар қозғалыс кезiнде бiр-бiрiмен өзара тартылыс және тебiлiс әсерiнде болады. 1.3 суретте молекулалық өзара әсерлесу күштерiнiң таралуы молекулалар арасындығы r арақашықтықтан тәуелдiлiгi келтiрiлген. Тартылу және тебiлу күштерi r-дан тәуелдiлiгi әртүрлi, сондықтан олардың қорытқы күшi нөлден өзгеше. Белгiлi бiр r = r0 арақашықтықта тебiлу күшi арасында тепе-теңдiк орнайды. Молекулалардың диаметрiмен салыстырылатын бұл арақашықтық тепе-теңдiк жағдайына сәйкес келедi. r < r0 болғанда тебiлу күшi тартылу күшiнен басым болады. Сондықтан молекулалар бiр-бiрiне ене алмайды. Олардың арасындағы арақашықтық r > r0 өскен сайын, молекулалардың тартылуы тебiлуiн жеңе бастaйды. Олардың ыршып кетуiне жол бермейдi. r >> r0 кезiнде, молекуларалық күштердiң әсерi болмайды.
Слайд 91.4 суретте молекулалардың Ep потенциалдық энергиясының r арақашықтықтан тәуелдiлiгi көрсетiлген. Орнықты
1.4-сурет
Слайд 10§ 1.4 Газдың молекулалық-кинетикалық теориясының негiзгi теңдеуi
Идеал газ деп молекулалардың өзара
Газ молекулалары барлық уақытта ретсiз жылулық қозғалыста болады, оның мөлшерлiк сипаттамасын молекуланың сызықты жылдамдығының орташа квадраты, дәлiрек айтқанда, кинетикалық энергиясының орта мәнi бередi. Жеке молекулалардың жылдамдықтары бiр-бiрiнен өзгеше болуы мүмкiн, бiрақ бұл жылдамдықтардың модулiнiң орташа мәнi белгiлi бiршама. Жеке молекулалардың жылдамдықтарын v1, v2, v3, . . . , vN арқылы белгiлеймiз. Сонда, жылдамдықтардың квадратының орташа мәнi келесi формуламен анықталады:
,
мұнда, N – газдағы молекулалардың жалпы саны. Екiншi жағынан . Қозғалыстың бейберекеттiгi әсерiнен молекулалардың барлық бағыттарда орынауыстыруы тең мүмкiндiкте. Сондықтан, жылдамдықтың проекциясының квадраттарының орташа мәндерi өзара тең: . Бұны ескере отырып, алатынымыз
(1.10)
Слайд 11Ендi идеал газдың ыдыс қабырғасына әсер ететiн күшiн табайық. Қоршаған ортаның
Идеал газ жағдайында Fn нормаль күштiң шамасы келесi өрнекпен анықталады:
(1.11)
мұнда, n – газ молекуласының концентрациясы (бiрлiк көлемдегi молекулалар саны: n=N/V), m0 - молекула массасы.
Слайд 12Бұл қатынастың қорытындысы.
Газдың барлық молекулаларда vx жылдамдық мәнi бiрдей бола
(1.12)
Егер арқылы молекуланың iлгерлемелi қозғалысының орташа кинетикалық энергиясын белгiлесек: , онда (1.12) тең-деуiн басқаша түрде жазуға болады
(1.13)
(1.12) немесе (1.13) қатынастар газдардың молекулалық-кинетикалық теориясының негiзгi теңдеулерi болып табылады. Олар, тiкелей өлшенетiн, макроскоптық шама – қысымды қозғалыстағы молекулаларды сипаттайтын микропараметрлармен байланыстырады.
Слайд 13§ 1.5 Газдың макропараметрлерi. Tемпература және оны өлшеу
Дененiң молекулалық-кинетикалық құрылымы ескерiлмегенде
Бұндай шамалар қатарына көлем V, қысым P, температура T және басқалар. Көлем мен қысым механикалық сипатталатын шамалар. Температура дененiң қызу дәрежесiн бередi, оның iшкi энергетикалық күйiн анықтайды.
Егер қандайда бiр оқшауланған жүйенi құрайтын денелер температурасы бастапқы уақытта әртүрлi болса, онда уақыттың келесi мезеттерiнде олар бiртiндеп теңесе бастайды да ақырында бiрдей болады, денелер арасында жылулық тепе-теңдiк орнайды.
Жүйенiң жылулық тепе-теңдiгi деп оның барлық макроскоптық параметрлерi қай уақытта да ұзақ өзгерiссiз қалуын айтады.
Слайд 14Осылайша, температура денелер жүйесiнiң жылулық тепе-теңдiк күйiн сипаттайды, атап айтқанда: өзара
Бұл Цельсийдiң градустер шкаласы деп аталады. 0-мен 100 нүктелерiнiң аралығын градус деп аталатын теңдей 100 бөлiкке бөлiнген (1.7 - сурет). Сұйық бағанының бiр бөлiкке жылжуы (орынауыстыруы) температураның 1 градус Цельсийге өзгеруiне сәйкес келедi. Әртүрлi сұйықтардың қыздырылғанда кеңуi (ұлғаюы) бiрдей болмағандықтан, термометрлерде оған сәйкес градуирленген.
Слайд 15§ 1.6 Температура - идеал газ молекуласының орташа кинетикалық энергиясының өлшемi
Барлық
Тәжiрибе көрсеткендей, θ=pV/N қатынасы температурадан басқа ештеңеден тәуелдi емес, сондықтан оны Т температураның бiрден-бiр өлшемi ретiнде қарастыруға болады.
θ = kТ немесе pV/N = kT, (1.14)
мұнда k – Больцман тұрақтысы деп аталатын пропорционалдық коэффициентi.
(1.14) теңдiгiмен анықталатын температура терiс шама болуы мүмкiн емес. Сондықтан ол абсолюттi температура деп аталады.
Слайд 16Температураның абсолюттi нөлi (Т = 0) деп молекулалық қозғалыстардың тоқтаған кезiн
(1.14) өрнегiн молекулалық-кинетикалық теорияның PV/N=2/3 түрiндегi негiзгi теңдеуiмен теңестiрiп
. (1.15)
Слайд 17Осылайша, абсолюттi температура газ молекулаларының жылулық қозғалысының орташа кинетикалық энергиясының өлшемi
(1.14) формуладан шығатыны мынадай өрнек
p = nkT. (1.16)
Қысым мен температура бiрдей болған жағдайда барлық газдардағы молекулалар концентрациясы да бiрдей болады (k тұрақтысы газдың қасиетiнен тәуелсiз). Басқаша айтқанда Авогадро заңының орындалуы байқалады: көлемдерi бiрдей газдарда қысым мен температура бiрдей болған жағдайда олардағы молекулалар саны да бiрдей болады.
Слайд 18§ 1.7 Газ молекуласының жылдамдығы. Штерн тәжiрибесi
Газ температурасы белгiлi болса, онда
(1.17)
Есептеуден байқалатыны,
молекулалардың жылдамдығы жоғары. Оларды салыстыру мүмкiн емес, мысалға, еркiн диффузия жылдамдығымен салыстырғанда. Соқтығысудың бейберекеттiгiнiң әсерiнен молекула траекториясының түзу сызықты бөлiктерiнде ғана жылдамдығы жоғары мәнге ие. Жалпы оның қандайда бiр бағытта орынауыстыруы салыстырмалы жоғары емес.
Арнайы тәжiрибе арқылы бұл жылдамдықты өлшеуге және есептелген мәнiмен салыстыруға болады. (1.12) формуласының дұрыстығын алғаш рет О.Штерн тәжiрибесiмен дәлелдендi. Штерн тәжiрибесiнiң жетiлдiрiлген түрi демонстрациялық моделде келтiрiлген (1.9 -сурет).
1.9-сурет
Слайд 19§ 1.8 Больцман тұрақтысы. Клайперон-Менделеевтiң күй теңдеуi
Температура үшiн pV/N = kT
k = 1.38·10-23Дж/К. (1.18)
Бұл коэффициент Больцман тұрақтысы деп аталады. Ол энергетикалық (Дж) өлшем бiрлiкпен анықталатын θ температураны, өлшем бiрлiгi Кельвинмен анықталатын, Т температурамен байланыстырады.
Слайд 20Молекулалық кинетикалық теорияның негiзгi теңдеуi p қысым, V көлем және T
pV = mkNAT/M. (1.19)
Больцман тұрақтысының k Авогадро санына NA көбейтiндiсiн универсал газ тұрақтысы деп атап, R әрпiмен белгiлейдi:
R = k NA = 8.31·103 Дж/(кмоль·К). (1.20)
Бұл енгiзiлген R тұрақтыны тағы да пайдаланып кез келген массасы m үшiн идеал газ күйiнiң теңдеуiн аламыз:
pV = mRT/M. (1.21)
Бұл Менделеев-Клапейронның күй теңдеуi деп аталады. Кейде бұл теңдеу алғашқы формасында қолданылады:
P1V1/T1 = p2V2/T2 = const, (1.22)
мұндағы 1 және 2 индекстерi газдың мүмкiн болатын кез келген екi күйiнiң параметрлерiне сәйкес.
Слайд 21§ 1.9 Газдағы изопроцесстер және олардың графиктерi.
Параметрлерiнiң бiрiнiң шамасы өзгерiссiз өтетiн
Идеал газ күйiнiң теңдеуiне сүйенiп изопроцестердiң негiзгi түрлерiнiң физикалық құбылыстарын қарастырайық.
Температура тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изотермиялық процесс деп атайды. Бұл процесс Бойль - Мариотт заңмен жазылады:
PV = const
Газ температурасын тұрақты ұстау үшiн, оның температурасын өзгертпейтiндей етiп жылуалмасып тұратын жүйе – термостат қажет. Әйтпесе, газ сығылғанда немесе созылғанда оның температурасының өзгерiсi елеулi.Изотермиялық процестiң (P,V) жазықтығындағы графигi, мзотерма деп аталатын, гиперболаны бередi (1.10 - сурет).
Слайд 22Қысым тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изобаралық процесс
Көлем тұрақты болған кезде термодинамикалық жүйе күйiнiң өзгеру процесiн изохоралық процесс деп атайды. Егер газ герметикалық ыдыста болса, онда газ көлемi тұрақты болады. Изохоралық процестiң (P,T) жазықтығындағы графигi, мзохора деп аталатын, түзу сызықты бередi (1.12 - сурет).