- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Баллистическое движение
Содержание
- 1. Презентация по физике на тему Баллистическое движение
- 2. Балли́стика (от греч. βάλλειν — бросать) — наука о движении тел, брошенных
- 3. Слайд 3
- 4. История баллистикиТарталья, 1537Г.ГалилейИ.Ньютон, 1687Б.Робинс, 1742Гуттон, Ломбард, 1797Обенгейм, 1814Магнус, Пуассон, Дидион, с 1820К.Рунге и М.Кутт, 1900
- 5. Баллистическая траектория — это траектория, по которой движется тело,
- 6. Зависимость формы траектории от угла бросания Угол,
- 7. При полете пули в воздухе угол наибольшей
- 8. При изучении движения пули в воздухе применяют
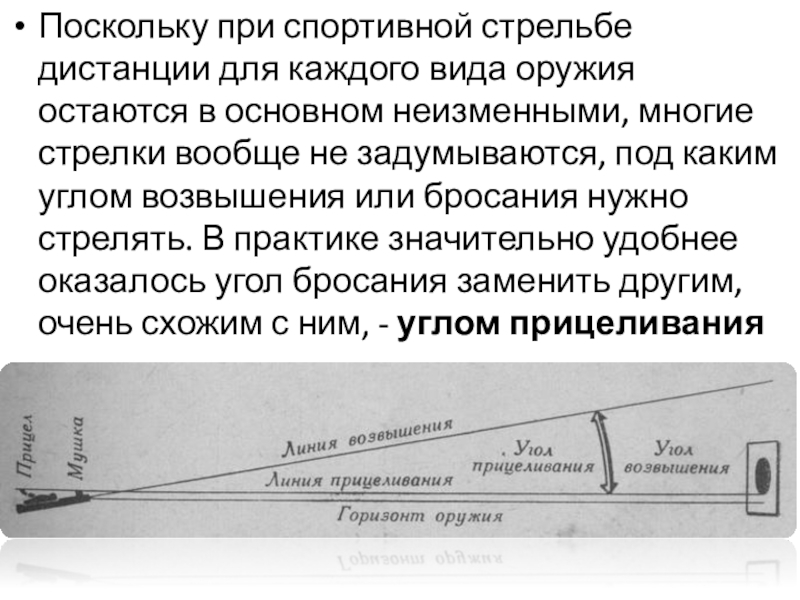
- 9. Поскольку при спортивной стрельбе дистанции для каждого
- 10. Зависимость формы траектории от величины начальной скорости
- 11. Влияние формы пули. Стремление увеличить дальность и
- 12. Влияние поперечной нагрузки. Чем тяжелее пуля, тем
- 13. Поперечная нагрузка тем больше, чем больше вес
- 14. Зависимость траектории от метеорологических условийВлияние ветра. Встречный
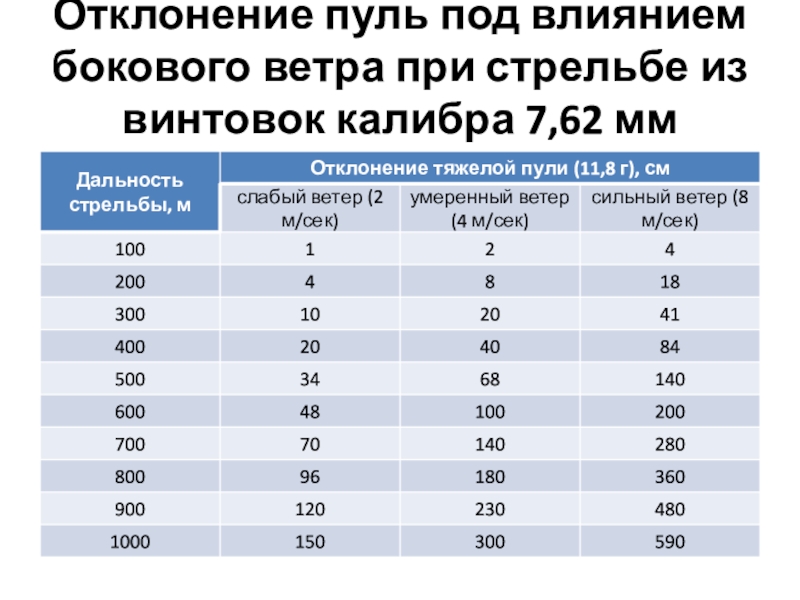
- 15. Отклонение пуль под влиянием бокового ветра при стрельбе из винтовок калибра 7,62 мм
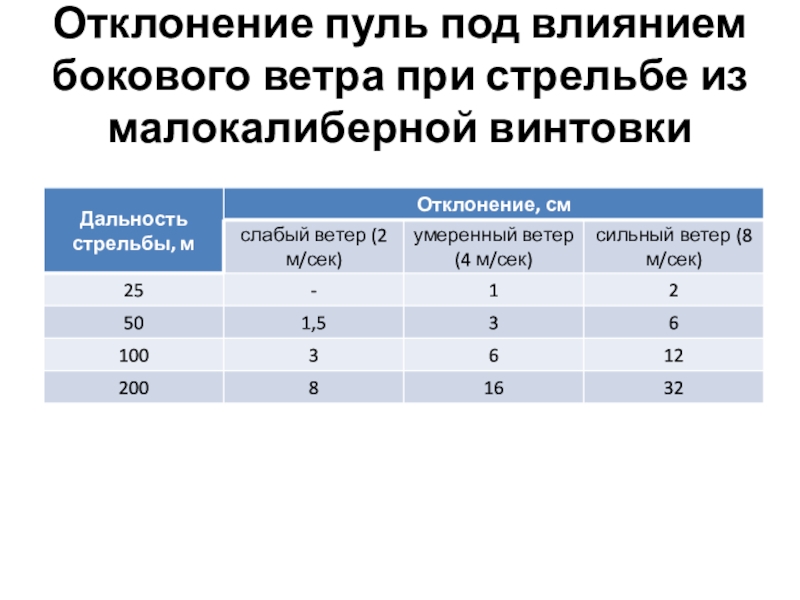
- 16. Отклонение пуль под влиянием бокового ветра при стрельбе из малокалиберной винтовки
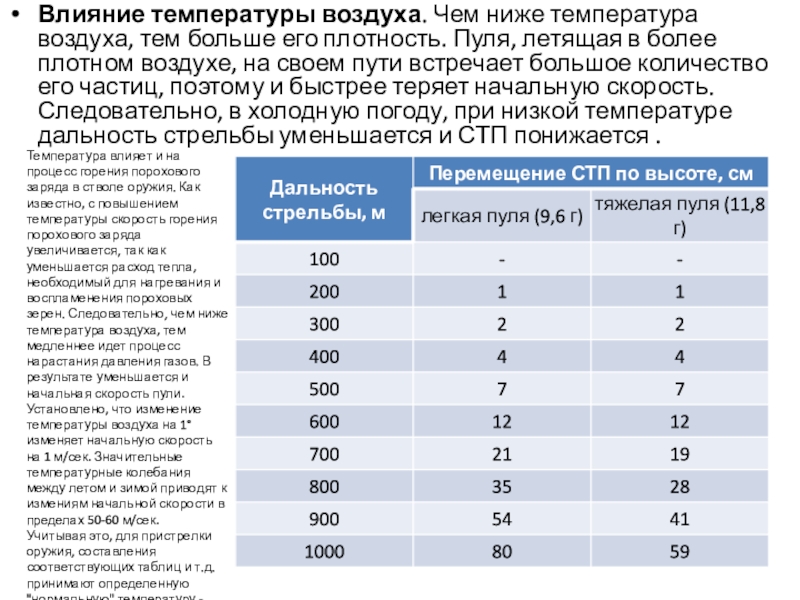
- 17. Влияние температуры воздуха. Чем ниже температура воздуха,
- 18. Рассеивание пульДаже при самых благоприятных условиях стрельбы
- 19. Слайд 19
- 20. Формулы, которым подчиняется свободное падение тел.Скорость в
- 21. Движение тела, брошенногопод углом к горизонтуухav0xv0yv0vvy=
- 22. h maxyxv0x=v0cosa Вдоль оси ОХ тело движется
- 23. v0x=v0cosa ухav0xv0yv0vvy=0lhgПо вертикали:Вдоль оси ОУ телодвижется равнозамедленно,подобно
- 24. h maxyxavvv=v0yv0yv0yv0xv0xvy =0v0v0x=v0cosa Вдоль оси ОУ тело
- 25. h maxyxv0уv0хv0уvуv0хvv0av=v0уvv=v0xНекоторые зависимости между величинамипри движении под
- 26. 150750450300600yxv0x=v0cosa Зависимость дальности полетаот угла, под которым
- 27. Движение тела, брошенного горизонтальноv0у=0,a=g ,gy= -g
- 28. h maxyxavvv=v0yv0yv0yv0xv0xvy =0v0Вдоль оси ОУ тело движется
- 29. Задача 1 Камень массой 200 г брошен с
- 30. Задача 2 Пушка и цель находятся на одном
- 31. Задача 3Прибор наблюдения обнаружил летящий снаряд и
- 32. Используя формулу для дальности полета тела, брошенного под углом к горизонту, получаем: L=(v02sin2α)/g=(2(v0cosα)(vosinα))/g=(2vxv0y)/g=(2l корень(vo2-(l/t)2))/gt=64000м Ответ: примерно 64 км.
Слайд 2 Балли́стика (от греч. βάλλειν — бросать) — наука о движении тел, брошенных в пространстве, основанная на математике и физике.
Слайд 4История баллистики
Тарталья, 1537
Г.Галилей
И.Ньютон, 1687
Б.Робинс, 1742
Гуттон, Ломбард, 1797
Обенгейм, 1814
Магнус, Пуассон, Дидион, с
К.Рунге и М.Кутт, 1900
Слайд 5 Баллистическая траектория — это траектория, по которой движется тело, обладающее некоторой начальной скоростью,
Без учёта сопротивления воздуха в центральном поле тяготения баллистическая траектория представляет собой кривую второго порядка. В зависимости от начальных скорости и направления, это будет дуга эллипса, один из фокусов которого совпадает с гравитационным центром Земли, или ветвь гиперболы; в частных случаях — окружность (первая космическая скорость), парабола (вторая космическая скорость), вертикальная прямая. Поскольку большая часть траектории баллистических ракет достаточно большой дальности (более 500 км) проходит в разреженных слоях атмосферы, где сопротивление воздуха практически отсутствует, их траектории на этом участке являются эллиптическими
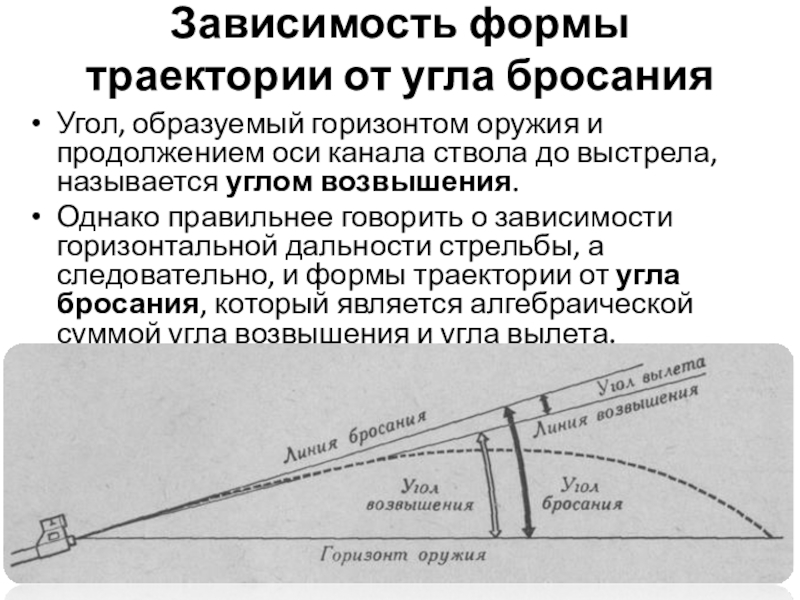
Слайд 6Зависимость формы траектории от угла бросания
Угол, образуемый горизонтом оружия и продолжением
Однако правильнее говорить о зависимости горизонтальной дальности стрельбы, а следовательно, и формы траектории от угла бросания, который является алгебраической суммой угла возвышения и угла вылета.
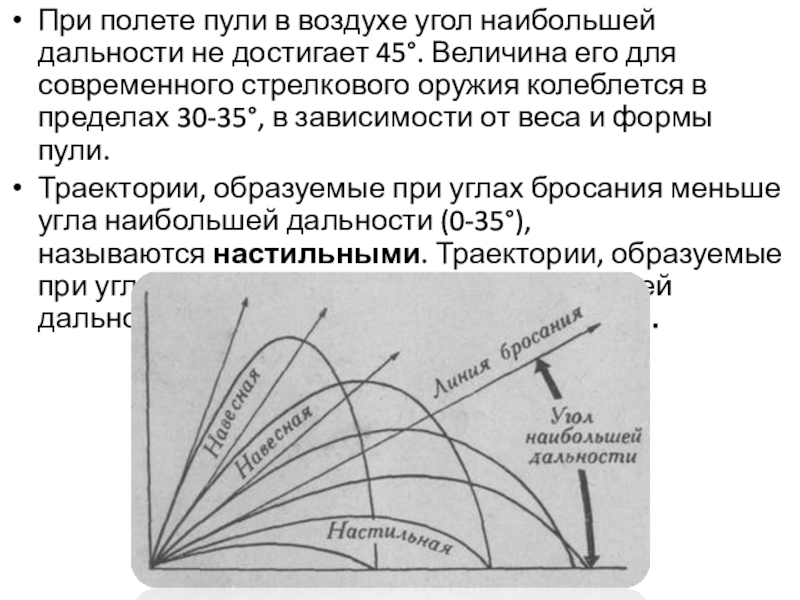
Слайд 7При полете пули в воздухе угол наибольшей дальности не достигает 45°.
Траектории, образуемые при углах бросания меньше угла наибольшей дальности (0-35°), называются настильными. Траектории, образуемые при углах бросания больше угла наибольшей дальности (35-90°), называются навесными.
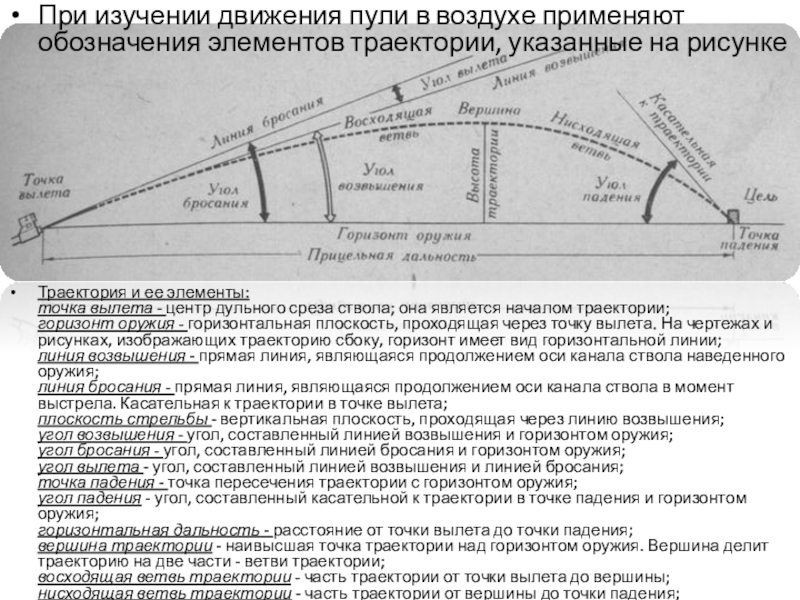
Слайд 8При изучении движения пули в воздухе применяют обозначения элементов траектории, указанные
Траектория и ее элементы:
точка вылета - центр дульного среза ствола; она является началом траектории;
горизонт оружия - горизонтальная плоскость, проходящая через точку вылета. На чертежах и рисунках, изображающих траекторию сбоку, горизонт имеет вид горизонтальной линии;
линия возвышения - прямая линия, являющаяся продолжением оси канала ствола наведенного оружия;
линия бросания - прямая линия, являющаяся продолжением оси канала ствола в момент выстрела. Касательная к траектории в точке вылета;
плоскость стрельбы - вертикальная плоскость, проходящая через линию возвышения;
угол возвышения - угол, составленный линией возвышения и горизонтом оружия;
угол бросания - угол, составленный линией бросания и горизонтом оружия;
угол вылета - угол, составленный линией возвышения и линией бросания;
точка падения - точка пересечения траектории с горизонтом оружия;
угол падения - угол, составленный касательной к траектории в точке падения и горизонтом оружия;
горизонтальная дальность - расстояние от точки вылета до точки падения;
вершина траектории - наивысшая точка траектории над горизонтом оружия. Вершина делит траекторию на две части - ветви траектории;
восходящая ветвь траектории - часть траектории от точки вылета до вершины;
нисходящая ветвь траектории - часть траектории от вершины до точки падения;
высота траектории - расстояние от вершины траектории до горизонта оружия.
Слайд 9Поскольку при спортивной стрельбе дистанции для каждого вида оружия остаются в
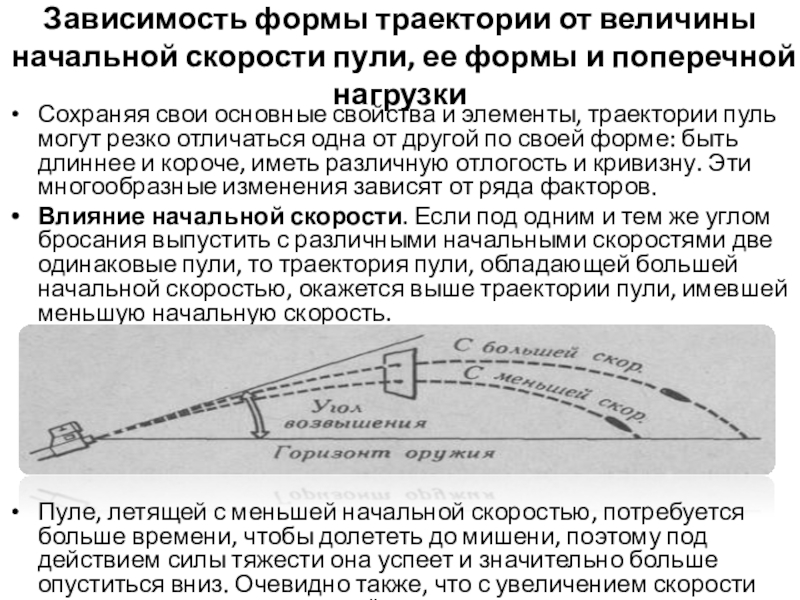
Слайд 10Зависимость формы траектории от величины начальной скорости пули, ее формы и
Сохраняя свои основные свойства и элементы, траектории пуль могут резко отличаться одна от другой по своей форме: быть длиннее и короче, иметь различную отлогость и кривизну. Эти многообразные изменения зависят от ряда факторов.
Влияние начальной скорости. Если под одним и тем же углом бросания выпустить с различными начальными скоростями две одинаковые пули, то траектория пули, обладающей большей начальной скоростью, окажется выше траектории пули, имевшей меньшую начальную скорость.
Пуле, летящей с меньшей начальной скоростью, потребуется больше времени, чтобы долететь до мишени, поэтому под действием силы тяжести она успеет и значительно больше опуститься вниз. Очевидно также, что с увеличением скорости увеличится и дальность ее лёта.
Слайд 11Влияние формы пули. Стремление увеличить дальность и меткость стрельбы требовало придать
Сгущение частиц воздуха перед головной частью пули и зона разреженного пространства позади нее являются основными факторами силы сопротивления воздуха. Головная волна, резко увеличивающая торможение пули, возникает при ее скорости, равной скорости звука или превышающей ее (свыше 340 м/сек).
Если скорость пули меньше скорости звука, то она летит у самого гребня звуковой волны, не испытывая чрезмерно большого сопротивления воздуха. Если же она больше скорости звука, пуля обгоняет все звуковые волны, образующиеся перед ее головной частью. В этом случае возникает головная баллистическая волна, которая значительно сильнее тормозит полет пули, отчего она быстро теряет скорость.
Если взглянуть на очертания головной волны и завихрения воздуха, которые возникают при движении различных по форме пуль ,то видно, что давление на головную часть пули тем меньше, чем острее ее форма. Зона разреженного пространства сзади пули тем меньше, чем больше скошена хвостовая ее часть; в этом случае сзади летящей пули будет также меньше завихрений.
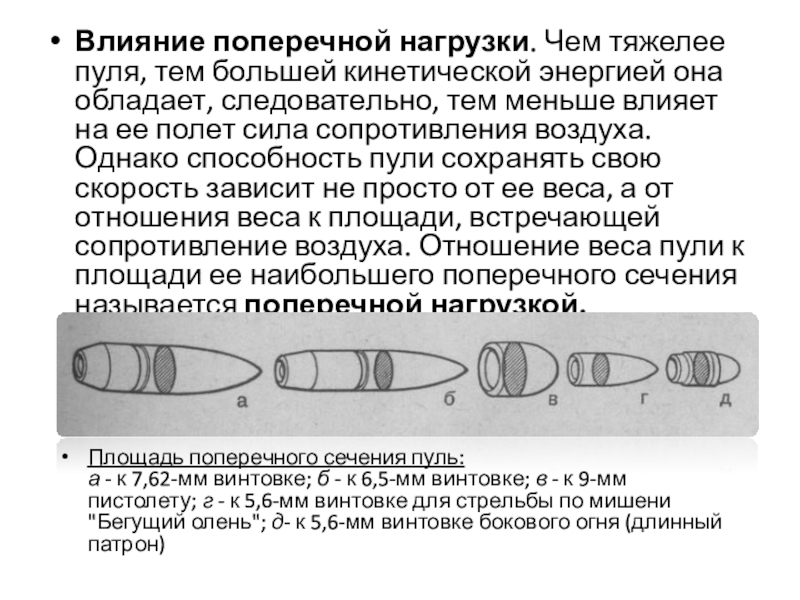
Слайд 12Влияние поперечной нагрузки. Чем тяжелее пуля, тем большей кинетической энергией она
Площадь поперечного сечения пуль:
а - к 7,62-мм винтовке; б - к 6,5-мм винтовке; в - к 9-мм пистолету; г - к 5,6-мм винтовке для стрельбы по мишени "Бегущий олень"; д- к 5,6-мм винтовке бокового огня (длинный патрон)
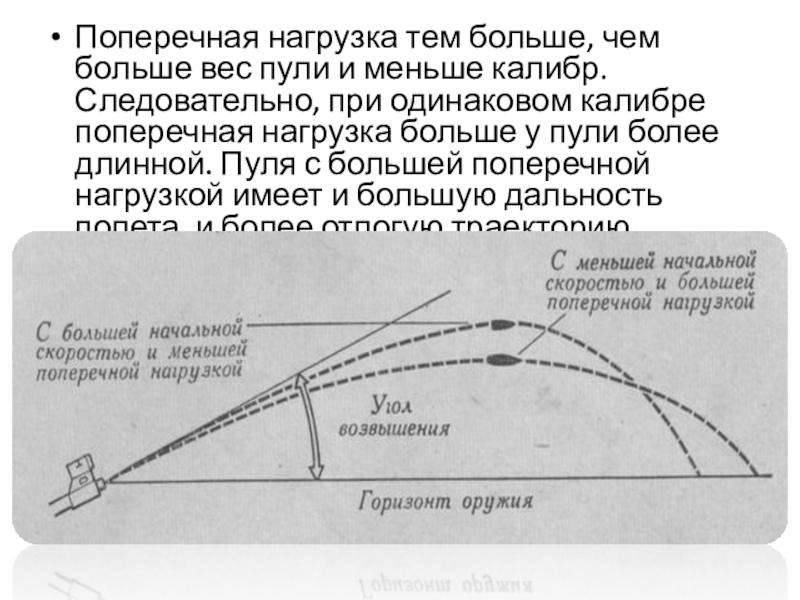
Слайд 13Поперечная нагрузка тем больше, чем больше вес пули и меньше калибр.
Слайд 14Зависимость траектории от метеорологических условий
Влияние ветра. Встречный и попутный ветры незначительно
Боковой же ветер значительно отклоняет пулю в сторону, причем даже при стрельбе на близкие расстояния.
Ветер характеризуется силой (скоростью) и направлением.
Сила ветра определяется его скоростью в метрах в секунду. В стрелковой практике различают ветер: слабый - 2 м/сек, умеренный - 4-5 м/сек и сильный - 8-10 м/сек.
Силу и направление ветра стрелки практически определяют по раазличным местным признакам: с помощью флага, по движению дыма, колебанию травы, кустов и деревьев и т.д.
Слайд 17Влияние температуры воздуха. Чем ниже температура воздуха, тем больше его плотность.
Температура влияет и на процесс горения порохового заряда в стволе оружия. Как известно, с повышением температуры скорость горения порохового заряда увеличивается, так как уменьшается расход тепла, необходимый для нагревания и воспламенения пороховых зерен. Следовательно, чем ниже температура воздуха, тем медленнее идет процесс нарастания давления газов. В результате уменьшается и начальная скорость пули.
Установлено, что изменение температуры воздуха на 1° изменяет начальную скорость на 1 м/сек. Значительные температурные колебания между летом и зимой приводят к измениям начальной скорости в пределах 50-60 м/сек.
Учитывая это, для пристрелки оружия, составления соответствующих таблиц и т.д. принимают определенную "нормальную" температуру - +15°.
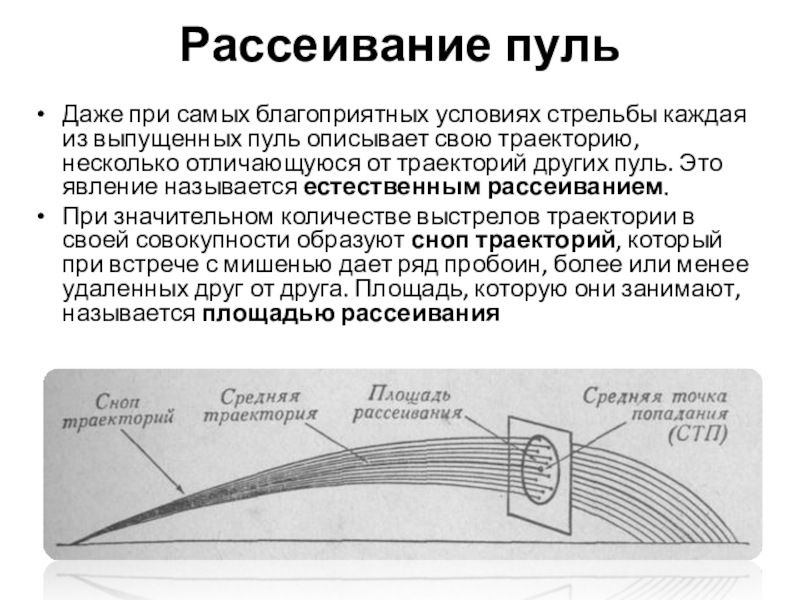
Слайд 18Рассеивание пуль
Даже при самых благоприятных условиях стрельбы каждая из выпущенных пуль
При значительном количестве выстрелов траектории в своей совокупности образуют сноп траекторий, который при встрече с мишенью дает ряд пробоин, более или менее удаленных друг от друга. Площадь, которую они занимают, называется площадью рассеивания
Слайд 20Формулы, которым подчиняется свободное падение тел.
Скорость в любой момент времени.
=
0
0
0
Путь, пройденный
v
+
=
0
gt
=
2
2
gt
h
v
+
=
2
0
2
gt
t
h
Модуль скорости в конце падения
=
2
gh
v
v
+
=
2
0
2
gh
Время свободного падения
=
2
g
h
t
0
v
v
v
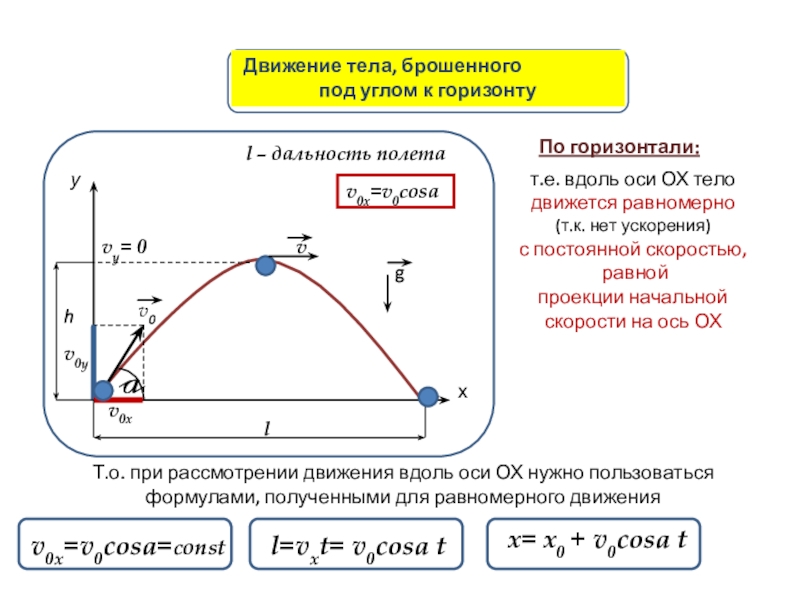
Слайд 21 Движение тела, брошенного
под углом к горизонту
у
х
a
v0x
v0y
v0
v
vy= 0
l
h
g
По горизонтали:
т.е. вдоль оси
движется равномерно
(т.к. нет ускорения)
с постоянной скоростью,
равной
проекции начальной
скорости на ось ОХ
Т.о. при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения
l=vxt= v0cosa t
x= x0 + v0cosa t
l – дальность полета
v0x=v0cosa
v0x=v0cosa=const
Слайд 22h max
y
x
v0x=v0cosa
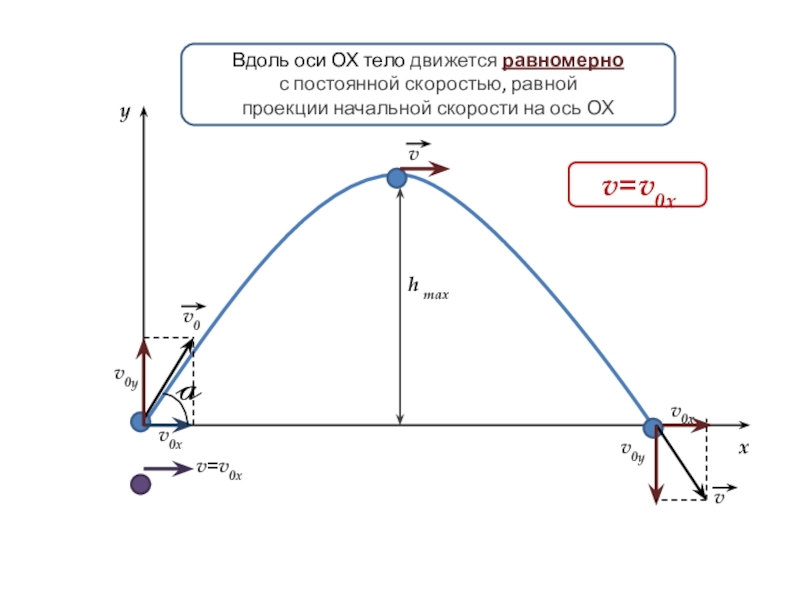
Вдоль оси ОХ тело движется равномерно
с постоянной скоростью, равной
проекции
v0х
v0
v=v0х
v0y
v0х
v0y
v
v
v0x=v0cosa
v=v0х
a
Слайд 23v0x=v0cosa
у
х
a
v0x
v0y
v0
v
vy=0
l
h
g
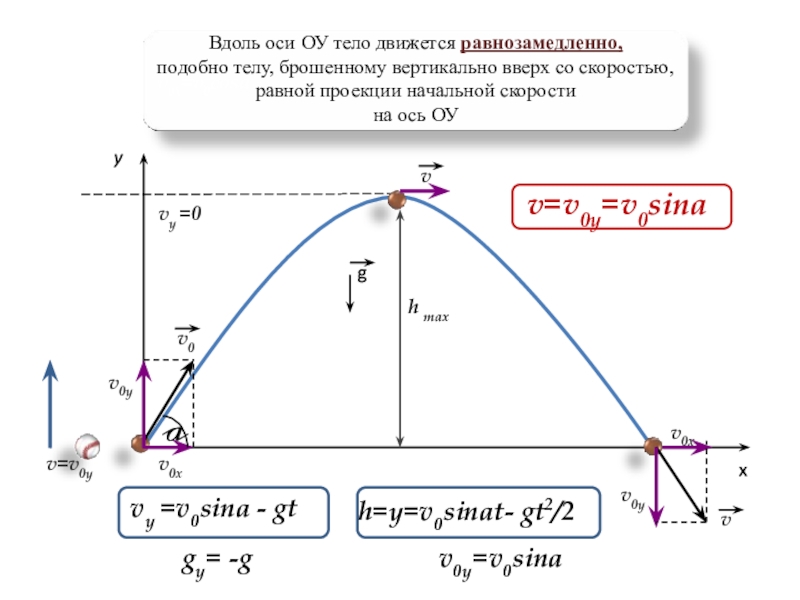
По вертикали:
Вдоль оси ОУ тело
движется равнозамедленно,
подобно телу, брошенному вертикально вверх
со скоростью, равной проекции начальной скорости на ось ОУ
h - максимальная высота
v0у=v0sina
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали
gy= -g ,
v0у=v0sina
=v0sina - gt
vy= v0y+gyt
y=y0+v0yt+gyt2/2 = v0sinat- gt2/2
=v0sina - gt
Слайд 24h max
y
x
a
v
v
v=v0y
v0y
v0y
v0x
v0x
vy =0
v0
v0x=v0cosa
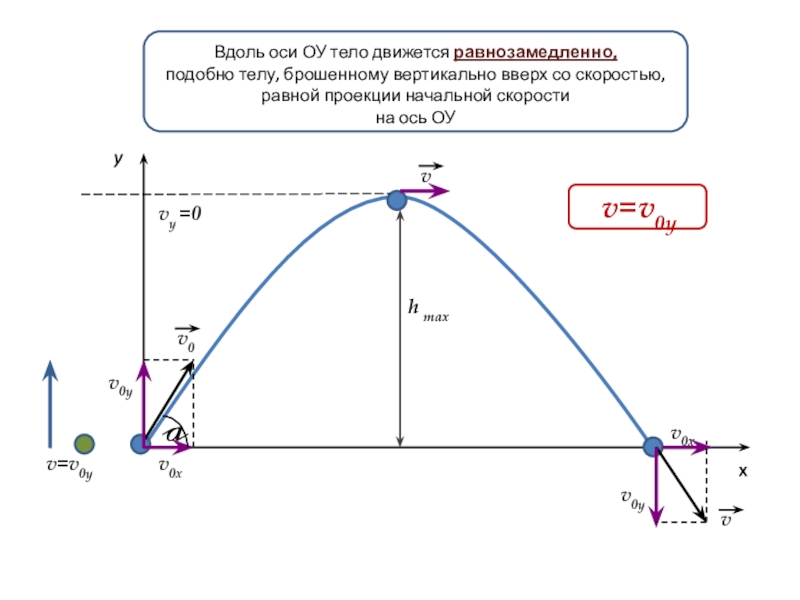
Вдоль оси ОУ тело движется равнозамедленно,
подобно телу, брошенному
на ось ОУ
v0x=v0cosa
v=v0y
Слайд 25h max
y
x
v0у
v0х
v0у
vу
v0х
v
v0
a
v=v0у
v
v=v0x
Некоторые зависимости между величинами
при движении под углом к горизонту
(баллистическом движении)
Время
больше времени
подъема тела на
максимальную высоту
t= 2tmax = 2v0sina/g
Дальность полета при одной и той же начальной скорости зависит от угла
l = x max= v02sin2a /g
v =
+ v0у2
v0x2
l = x max
Слайд 26150
750
450
300
600
y
x
v0x=v0cosa
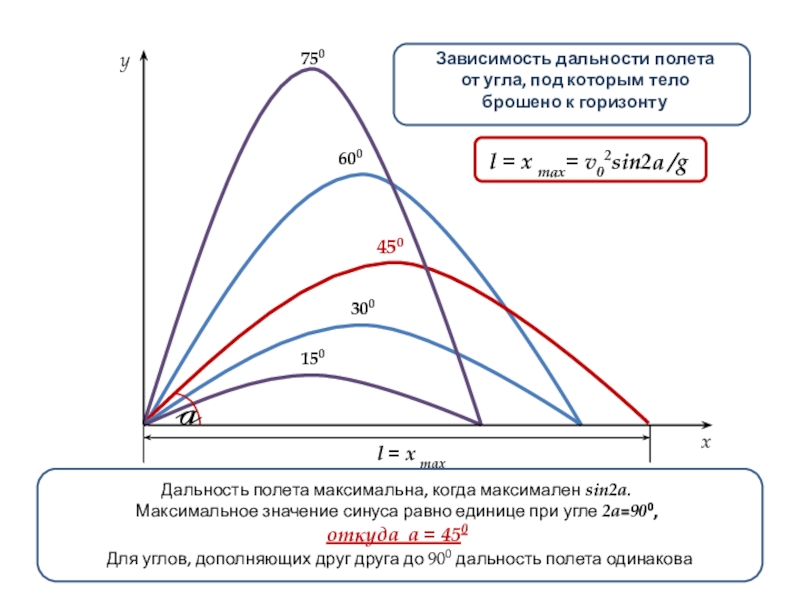
Зависимость дальности полета
от угла, под которым тело
брошено к горизонту
l
l = x max= v02sin2a /g
a
v0x=v0cosa
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900,
откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова
Слайд 27 Движение тела, брошенного
горизонтально
v0у=0,
a=g ,
gy= -g ,
y0 =h
s =h
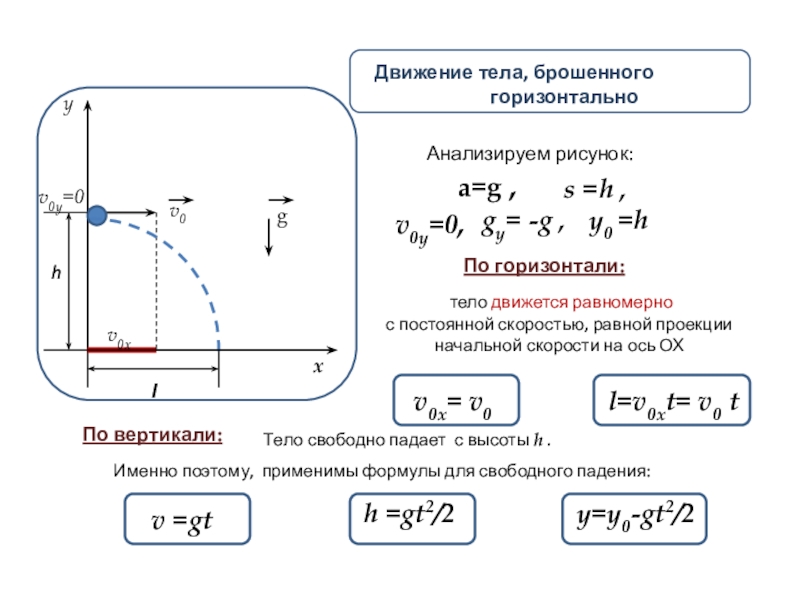
Анализируем рисунок:
По горизонтали:
тело движется равномерно
с постоянной скоростью, равной проекции начальной скорости на ось ОХ
v0x= v0
l=vxt= v0cosa t
l=v0xt= v0 t
По вертикали:
Тело свободно падает с высоты h .
Именно поэтому, применимы формулы для свободного падения:
v =gt
h =gt2/2
y=y0-gt2/2
v0
g
h
l
v0y=0
v0x
у
х
Слайд 28h max
y
x
a
v
v
v=v0y
v0y
v0y
v0x
v0x
vy =0
v0
Вдоль оси ОУ тело движется равнозамедленно,
подобно телу, брошенному вертикально
на ось ОУ
v0x=v0cosa
v=v0y=v0sina
gy= -g
v0у=v0sina
Слайд 29Задача 1
Камень массой 200 г брошен с горизонтальной поверхности под углом
Слайд 30Задача 2
Пушка и цель находятся на одном уровне на расстоянии l
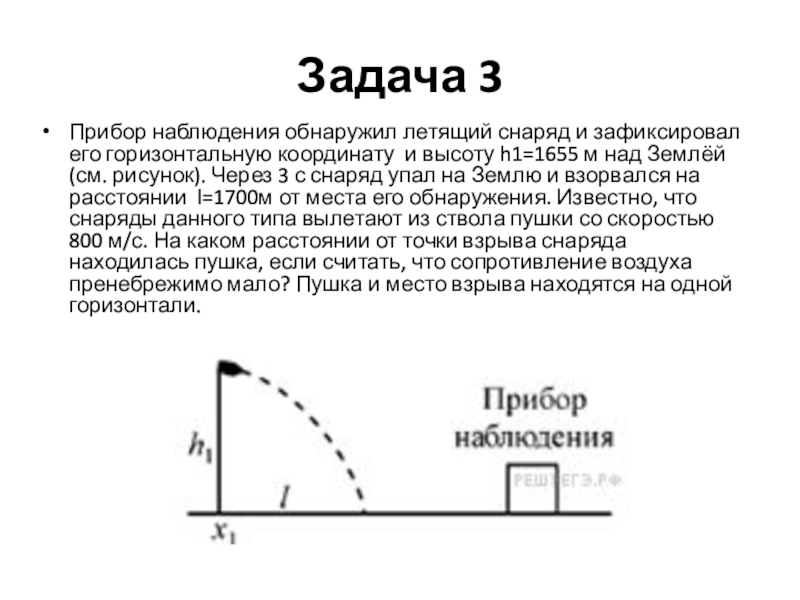
Слайд 31Задача 3
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и
Слайд 32 Используя формулу для дальности полета тела, брошенного под углом к горизонту,
L=(v02sin2α)/g=(2(v0cosα)(vosinα))/g=(2vxv0y)/g=(2l корень(vo2-(l/t)2))/gt=64000м
Ответ: примерно 64 км.