- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике Электронный задачник. Изопроцессы
Содержание
- 1. Презентация по физике Электронный задачник. Изопроцессы
- 2. ЗАДАЧИ Задача №1.Задача №2.Задача №8.Задача №9.Задача №4.Задача №5.Задача №10.Задача №3.Задача №7.Задача №11.Задача №6.
- 3. ЗАДАЧА №1
- 4. α2α10TPНа рисунке представлены две изохоры для газа
- 5. Найти:Дано:Решение:
- 6. Во втором случае: Исходя из выше написанного следует, что Ответ:
- 7. ЗАДАЧА №2
- 8. С газом некоторой массы был произведён замкнутый
- 9. 340TP21Решение. Используем для анализа процесса изображенного на
- 10. откуда следует, что на отрезке 3-4 объём
- 11. Ответ.1-2-оставался постоянным;2-3-увеличивался пропорционально Т;3-4-увеличивался;4-1-уменьшался пропорционально Т.
- 12. ЗАДАЧА №3
- 13. Начертить изотерму процесса для случая pV=40. Пользуясь
- 14. pV12342460
- 15. ЗАДАЧА №4
- 16. Как менялось температура идеального газа – увеличивалась
- 17. Решение.pV0нагрваниеохлаждениеКривая уравнения изотермы в координатах p, V
- 18. ЗАДАЧА №5
- 19. Идеальный газ совершает замкнутый процесс, изображенный на
- 20. 0р1234 Решение.Т1-2 изотермический , 2-3
- 21. pV01234
- 22. ЗАДАЧА №6
- 23. Тр01243Газ совершает замкнутый процесс. Какое количество теплоты
- 24. Cформулируем общий алгоритм решения этой задачи:
- 25. Решение:0pV4123В координатах (p,V) цикл обходится по часовой
- 26. При контакте с нагревателем система получает теплоа
- 27. от менее нагретого (холодного) тела забирается количество
- 28. а) если цикл соответствует тепловому двигателю (обход
- 29. где - температура более
- 30. ЗАДАЧА №7
- 31. Найдите работу, совершаемую одним молем идеального газа
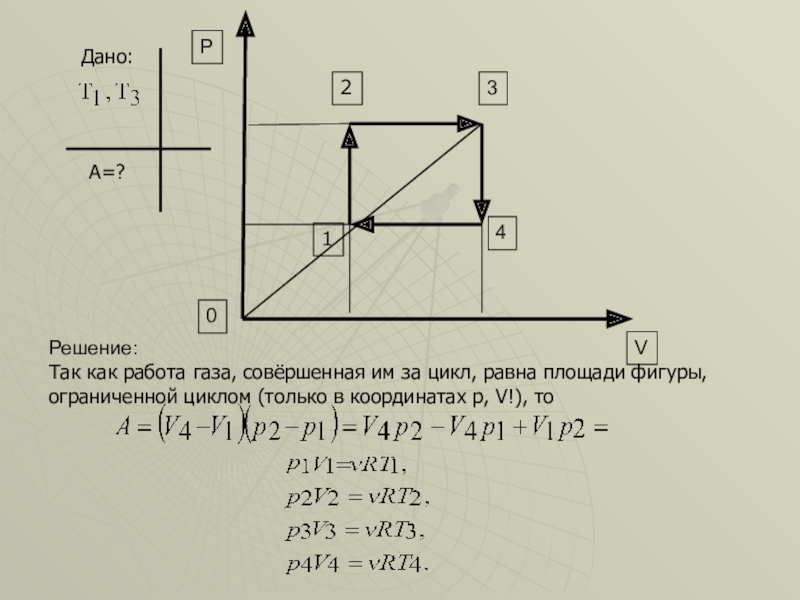
- 32. Дано:А=?340VP21Так как работа газа, совёршенная им за
- 33. В системе уравнений:(1)(2)(3)(4)Уменьшаем индексы:Из этого равенства, а
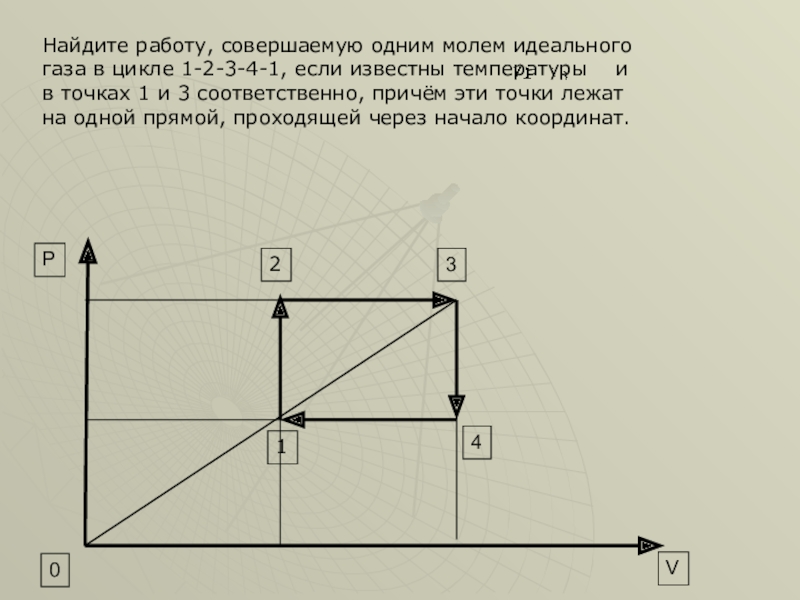
- 34. Так как точки 1 и 3 лежат
- 35. Ответ.
- 36. ЗАДАЧА №8
- 37. Может ли существовать такое вещество, которое можно
- 38. Решение:0pV12Идеальный газ не может служить примером такого
- 39. ЗАДАЧА №9
- 40. На рисунке показана теоретическая диаграмма работы компрессора
- 41. Решение:pV236547Работа за цикл изображается площадью фигуры 1
- 42. Так как точки 1 и 2 лежат
- 43. ЗАДАЧА №10
- 44. На рисунке дан график изменения состояния идеального
- 45. 0VT231Решение.Поскольку на осях координат не указан масштаб,
- 46. Переход 3 – 1 осуществляется при постоянном
- 47. Изохорный процесс при уменьшении температуры сопровождается уменьшением
- 48. Точка 3 должна находиться на изотерме
- 49. ЗАДАЧА №11
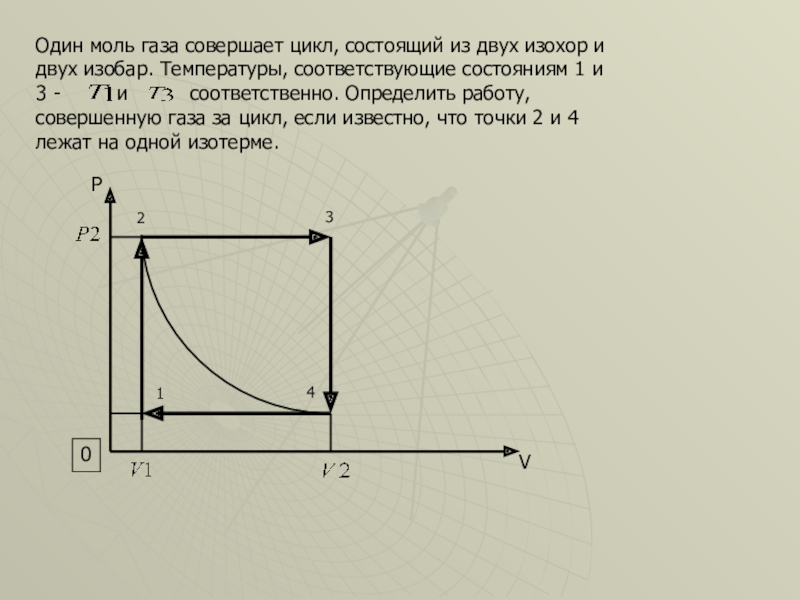
- 50. Один моль газа совершает цикл, состоящий из
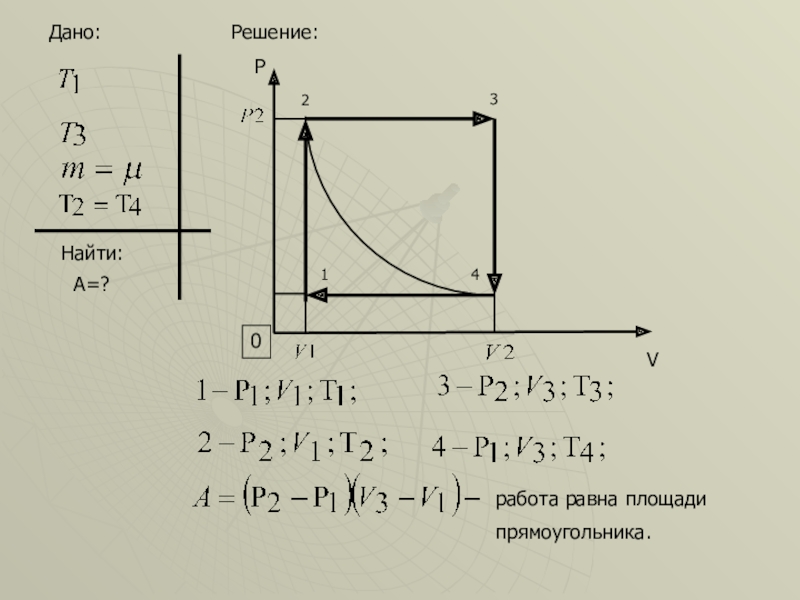
- 51. Дано:Найти:А=?PV01234Решение:работа равна площадипрямоугольника.
- 52. Так как (1)Уравнение Клайперона-Менделеева:( так как
- 53. Ответ:
Слайд 2ЗАДАЧИ
Задача №1.
Задача №2.
Задача №8.
Задача №9.
Задача №4.
Задача №5.
Задача №10.
Задача №3.
Задача №7.
Задача
Задача №6.
Слайд 4
α2
α1
0
T
P
На рисунке представлены две изохоры для газа одной и той же
и ?
Слайд 5Найти:
Дано:
Решение:
Уравнение Менделеева -
Зная, что
, можно записать в виде
В первом случае:
Отсюда следует, что
α2
α1
0
T
P
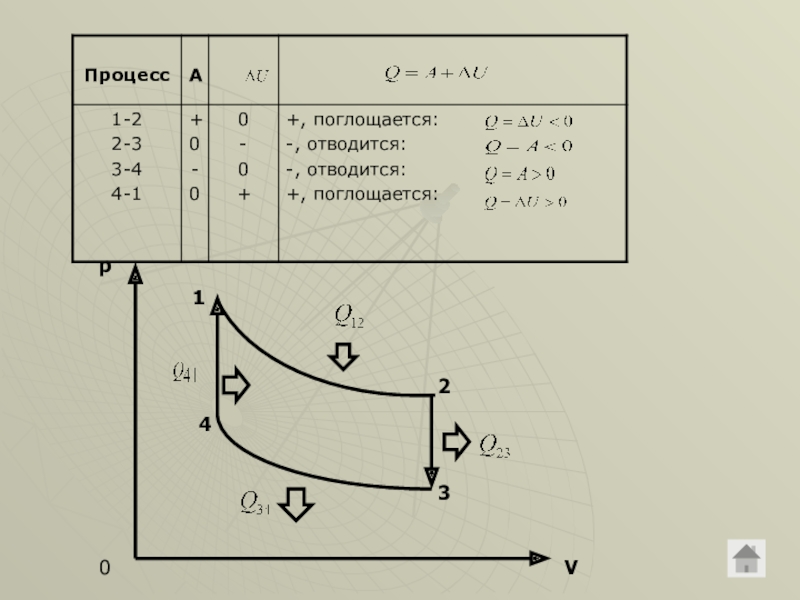
Слайд 8С газом некоторой массы был произведён замкнутый процесс, изображенный на рисунке.
3
4
0
T
P
2
1
Слайд 93
4
0
T
P
2
1
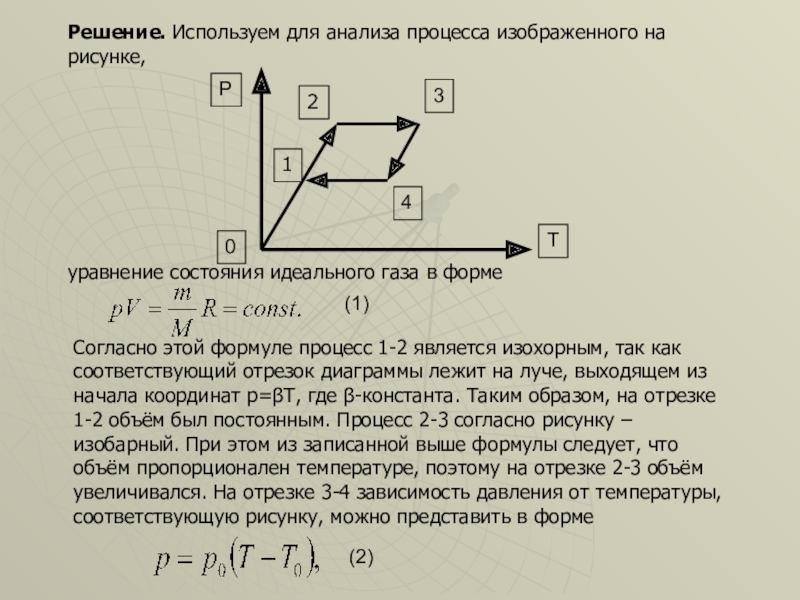
Решение. Используем для анализа процесса изображенного на рисунке,
уравнение состояния идеального газа
Согласно этой формуле процесс 1-2 является изохорным, так как соответствующий отрезок диаграммы лежит на луче, выходящем из начала координат p=βТ, где β-константа. Таким образом, на отрезке 1-2 объём был постоянным. Процесс 2-3 согласно рисунку – изобарный. При этом из записанной выше формулы следует, что объём пропорционален температуре, поэтому на отрезке 2-3 объём увеличивался. На отрезке 3-4 зависимость давления от температуры, соответствующую рисунку, можно представить в форме
(1)
(2)
Слайд 10откуда следует, что на отрезке 3-4 объём увеличился из-за уменьшения температуры.Отрезок
где и - положительные константы. При этом, согласно формуле (1), зависимость объёма от температуры с учётом изменения давления (2) имеет вид:
(3)
Слайд 11Ответ.1-2-оставался постоянным;
2-3-увеличивался пропорционально Т;
3-4-увеличивался;
4-1-уменьшался пропорционально Т.
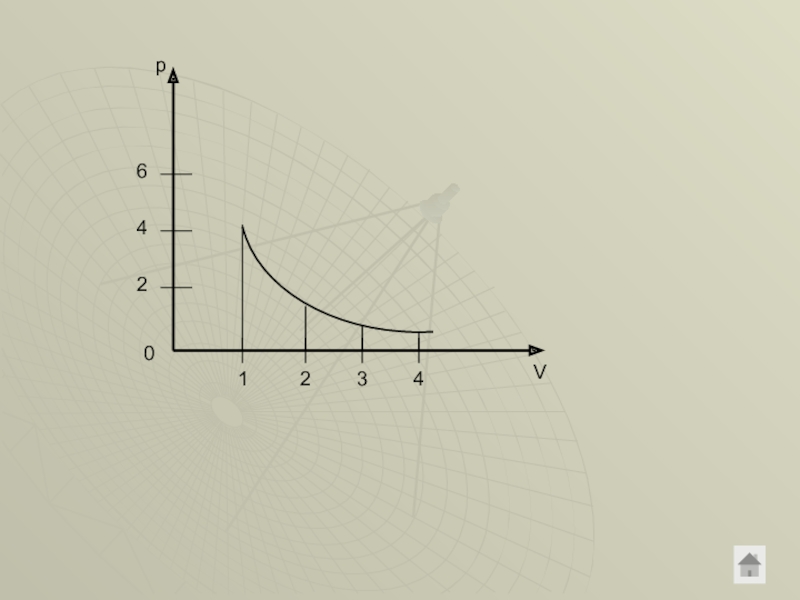
Слайд 13Начертить изотерму процесса для случая pV=40. Пользуясь графиком ответить на вопрос:
Дано:
pV=40
Т=const
p(V)=?
Решение:
Найти:
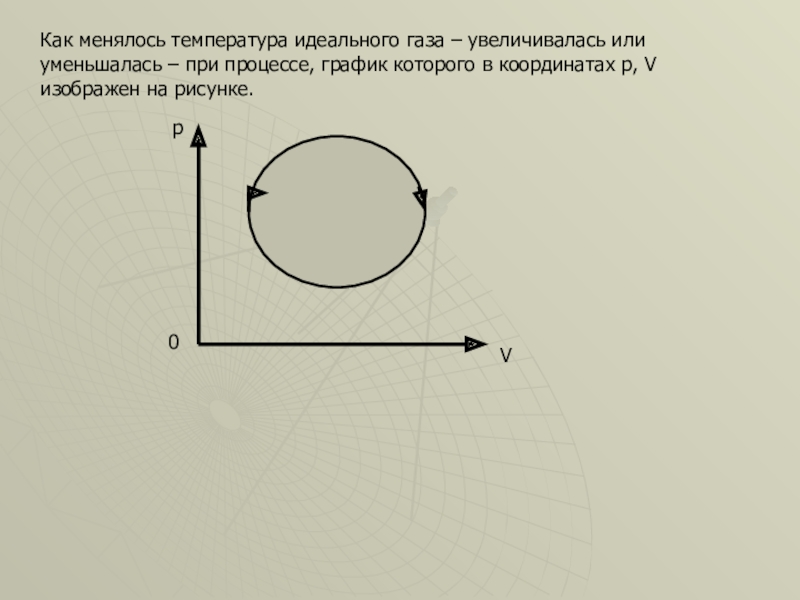
Слайд 16Как менялось температура идеального газа – увеличивалась или уменьшалась – при
p
V
0
Слайд 17Решение.
p
V
0
нагрвание
охлаждение
Кривая уравнения изотермы в координатах p, V – гипербола; pV=const, причем
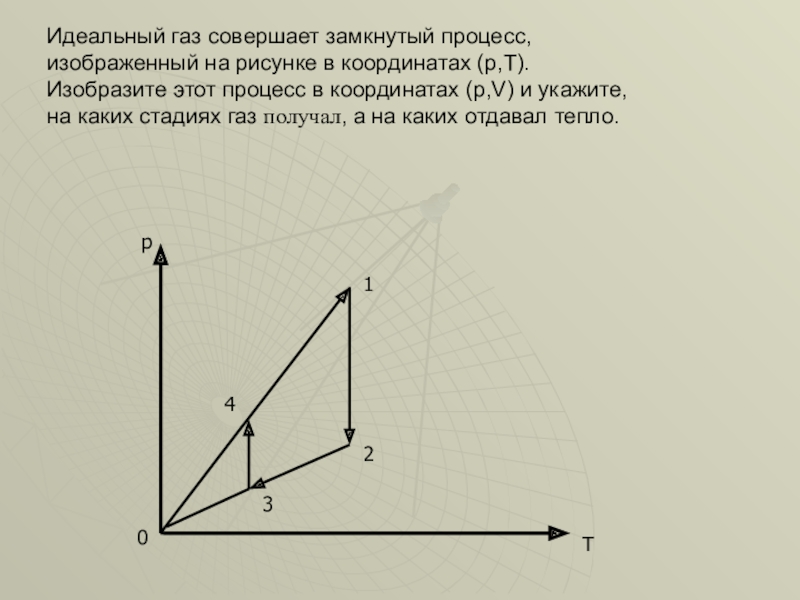
Слайд 19Идеальный газ совершает замкнутый процесс, изображенный на рисунке в координатах (p,T).Изобразите
0
р
Т
1
2
3
4
Слайд 200
р
1
2
3
4
Решение.
Т
1-2 изотермический , 2-3 изохорический, 3-4 изотермический, 4-1
, количества теплоты .
Слайд 23Т
р
0
1
2
4
3
Газ совершает замкнутый процесс. Какое количество теплоты больше: полученное от нагревателя
Слайд 24 Cформулируем общий алгоритм решения этой задачи:
перевести цикл в координаты
установить направление обхода цикла и тип машины; оценить величины поглощенного и отданного количеств теплоты и общую работу;
рассчитать КПД машины.
Слайд 25
Решение:
0
p
V
4
1
2
3
В координатах (p,V) цикл обходится по часовой стрелке, следовательно, мы имеем
Для полноты картины приведем таблицу, отвечающую разным участкам цикла: изохоры 1-2, изобары 2-3, изохоры 3-4, изотермы
4-1.
Слайд 26При контакте с нагревателем система получает тепло
а тепло
отдает холодильнику.
Если цикл запустить
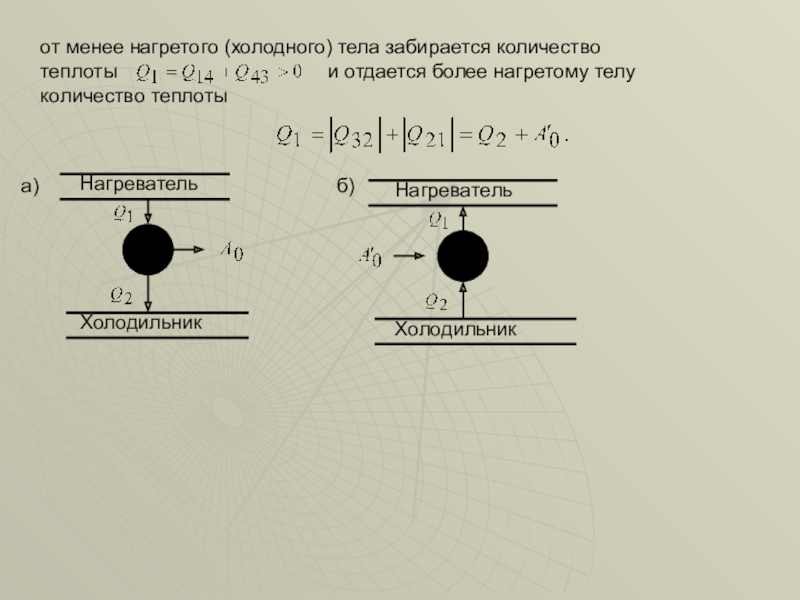
Слайд 27от менее нагретого (холодного) тела забирается количество теплоты
Нагреватель
Холодильник
а)
Нагреватель
Холодильник
б)
Слайд 28а) если цикл соответствует тепловому двигателю (обход по часовой стрелке), КПД
(1)
б) если цикл соответствует идеальной тепловой машине (прямому циклу Карно), то её КПД
где и - температуры нагревателя и холодильника соответственно;
в) если цикл соответствует холодильной машине (обход против часовой стрелки), то ее КПД (точнее, холодильный коэффициент) определяется по формуле:
(2)
Слайд 29где - температура более нагретого тела,
г) если цикл соответствует идеальной холодильной машине (обратному циклу Карно ), то ее холодильный коэффициент
д) если обратный цикл соответствует так называемому тепловому насосу, то КПД теплового насоса
для идеального цикла Карно:
Слайд 31Найдите работу, совершаемую одним молем идеального газа в цикле 1-2-3-4-1, если
3
4
0
V
P
2
1
Слайд 32Дано:
А=?
3
4
0
V
P
2
1
Так как работа газа, совёршенная им за цикл, равна площади фигуры,
Решение:
Слайд 33В системе уравнений:
(1)
(2)
(3)
(4)
Уменьшаем индексы:
Из этого равенства, а также из второго и
Исходя из уравнения Менделеева-Клайперона, можно записать:
Слайд 34Так как точки 1 и 3 лежат на прямой, проходящей через
или после следующего уменьшения индекса,
Из этого равенства, а также из второго и четвёртого уравнений последней системы сразу вытекает:
Перемножив почленно первое и третье, а затем второе и четвёртое уравнения системы:
Получим:
, или
Отсюда
Слайд 37Может ли существовать такое вещество, которое можно перевести из некого начального
0
p
V
1
2
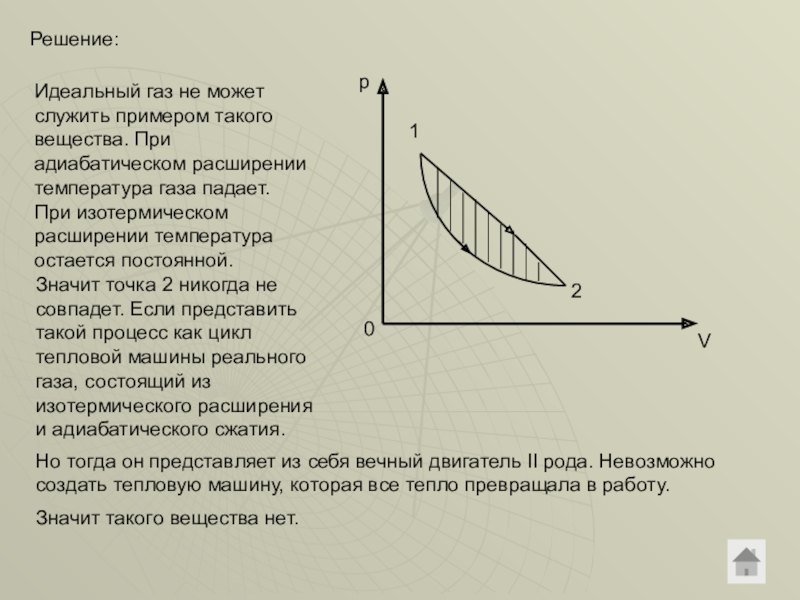
Слайд 38Решение:
0
p
V
1
2
Идеальный газ не может служить примером такого вещества. При адиабатическом расширении
Значит точка 2 никогда не совпадет. Если представить такой процесс как цикл тепловой машины реального газа, состоящий из изотермического расширения и адиабатического сжатия.
Но тогда он представляет из себя вечный двигатель II рода. Невозможно создать тепловую машину, которая все тепло превращала в работу.
Значит такого вещества нет.
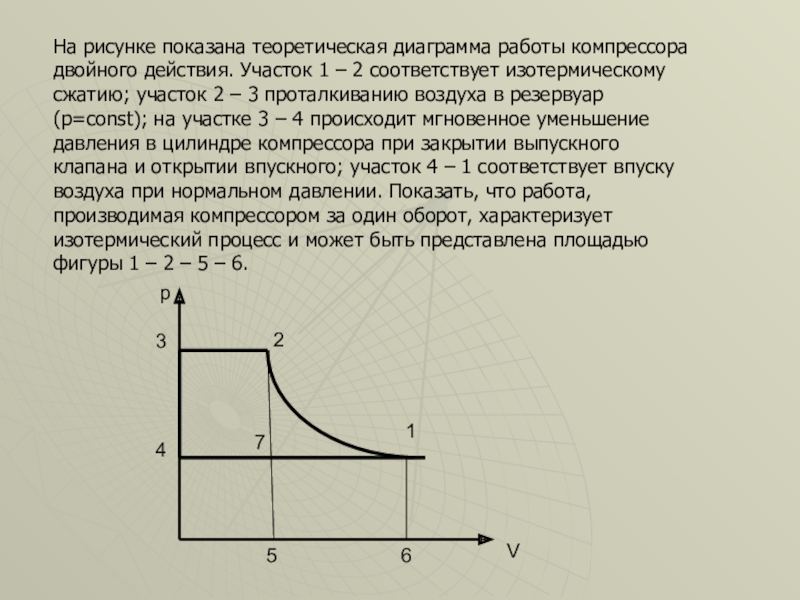
Слайд 40На рисунке показана теоретическая диаграмма работы компрессора двойного действия. Участок 1
p
V
2
3
1
6
5
4
7
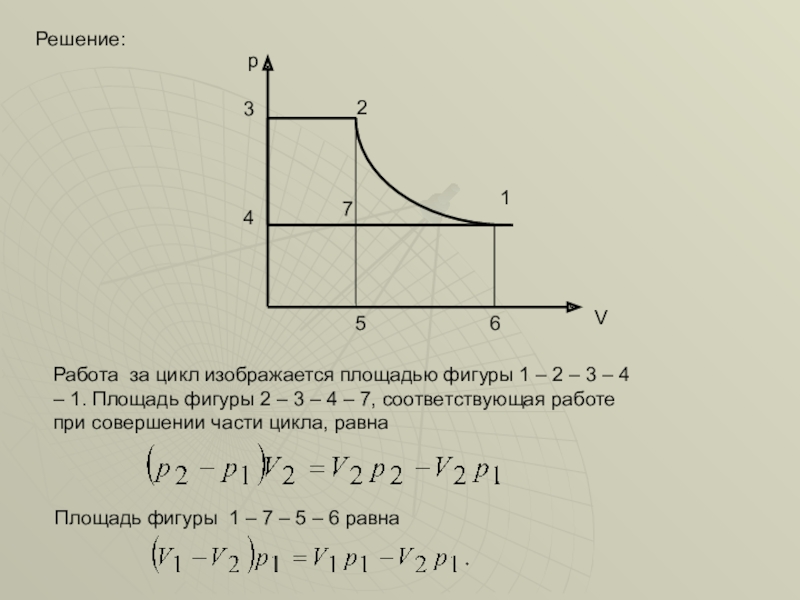
Слайд 41Решение:
p
V
2
3
6
5
4
7
Работа за цикл изображается площадью фигуры 1 – 2 – 3
Площадь фигуры 1 – 7 – 5 – 6 равна
1
Слайд 42Так как точки 1 и 2 лежат на одной изотерме, то
Следовательно,
то есть за один оборот равна работе при изотермическом процессе.
Слайд 44На рисунке дан график изменения состояния идеального газа в координатных осях
0
V
T
2
3
1
Слайд 450
V
T
2
3
1
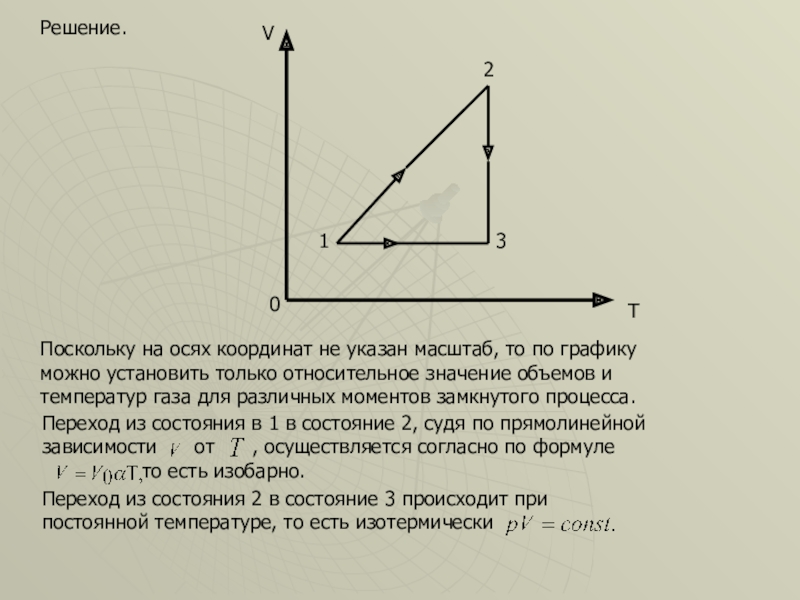
Решение.
Поскольку на осях координат не указан масштаб, то по графику можно
Переход из состояния в 1 в состояние 2, судя по прямолинейной зависимости от , осуществляется согласно по формуле
то есть изобарно.
Переход из состояния 2 в состояние 3 происходит при постоянной температуре, то есть изотермически
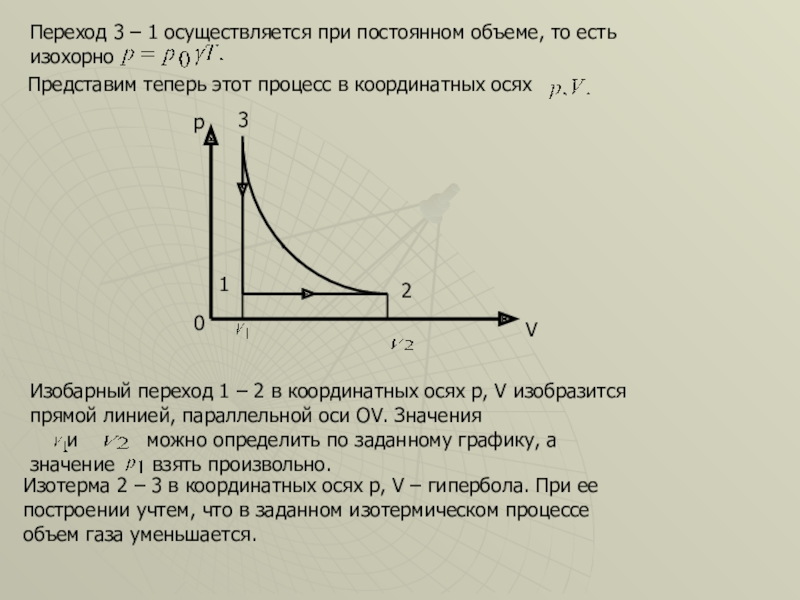
Слайд 46Переход 3 – 1 осуществляется при постоянном объеме, то есть изохорно
Представим теперь этот процесс в координатных осях
p
0
V
3
2
1
Изобарный переход 1 – 2 в координатных осях p, V изобразится прямой линией, параллельной оси ОV. Значения
и можно определить по заданному графику, а значение взять произвольно.
Изотерма 2 – 3 в координатных осях p, V – гипербола. При ее построении учтем, что в заданном изотермическом процессе объем газа уменьшается.
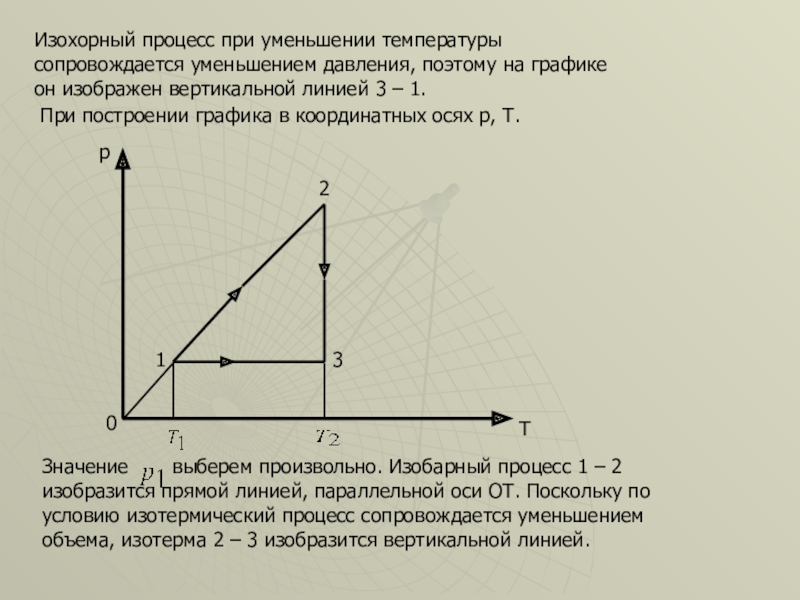
Слайд 47Изохорный процесс при уменьшении температуры сопровождается уменьшением давления, поэтому на графике
При построении графика в координатных осях p, T.
0
p
T
2
3
1
Значение выберем произвольно. Изобарный процесс 1 – 2 изобразится прямой линией, параллельной оси ОТ. Поскольку по условию изотермический процесс сопровождается уменьшением объема, изотерма 2 – 3 изобразится вертикальной линией.
Слайд 48Точка 3 должна находиться на изотерме -
После этого ясно, что изохорный процесс изобразится отрезком 3 – 1.
Слайд 50Один моль газа совершает цикл, состоящий из двух изохор и двух
P
V
0
1
2
3
4
Слайд 52Так как
(1)
Уравнение Клайперона-Менделеева:
( так как
(2)
(3)
(4)
Из
Преобразуем уравнение для работы: