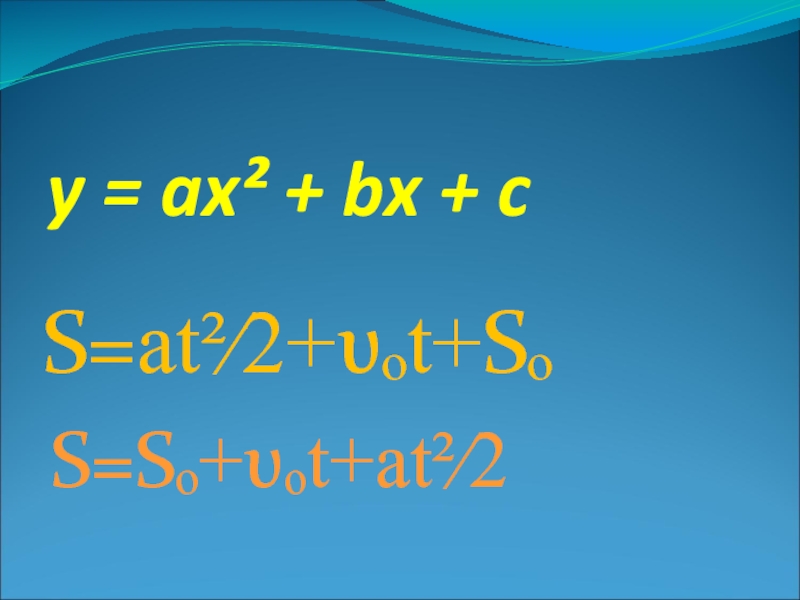математики- это только природоведение»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к интегрированному занятию по подготовке к ГИА и ЕГЭ по математике и физике
Содержание
- 1. Презентация к интегрированному занятию по подготовке к ГИА и ЕГЭ по математике и физике
- 2. Графическое решение задач
- 3. Задание 1 Постройте графическую зависимость двух переменных на компьютере y=5x²+3x-2
- 4. Слайд 4
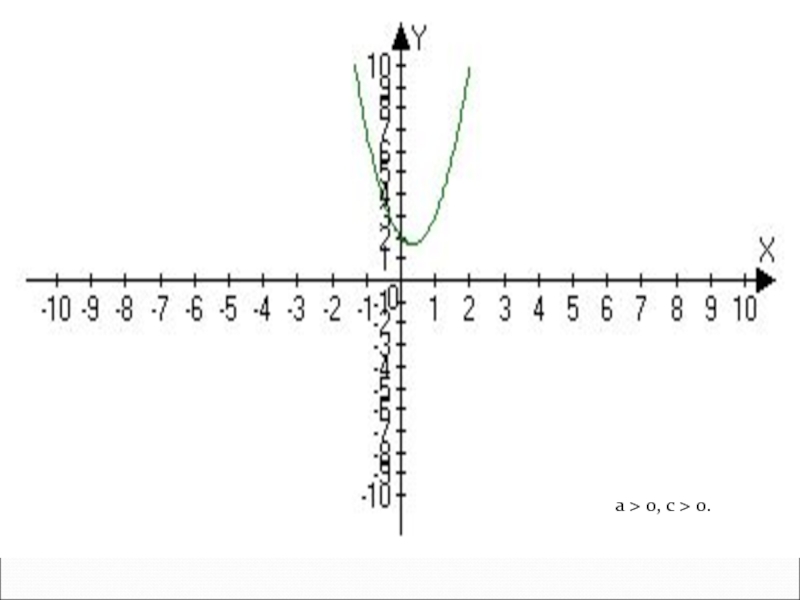
- 5. Задание 2 Постройте зависимость двух переменных у=3x²-2x+2
- 6. а > 0, с > 0.
- 7. Постройте зависимость двух переменных у=-x²+4x-3
- 8. Слайд 8
- 9. y = ax² + bx + c S=Sₒ+υₒt+at²∕2S=at²∕2+υₒt+Sₒ
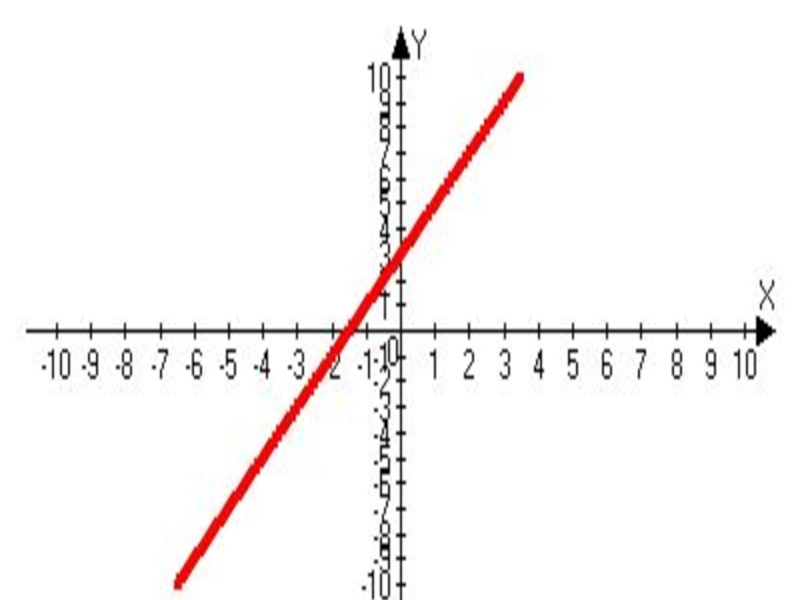
- 10. По рисунку составьте уравнение зависимости координаты тела
- 11. Найдите координату тела через 2,5с х = 2
- 12. Слайд 12
- 13. Требуется, как можно больше почерпнуть информации из графика
- 14. Задание 6. Пользуясь графиками, изображенными на рисунке,
- 15. График II.V0 = 2 м/с;a = 0,75 м/с².Движение
- 16. График III.V0 = v = 3 м/с; a
- 17. График IV.V0 = 7 м/с;a = - 1,2
- 18. Задача.Из двух точек А и В, расположенных
- 19. 1 способ (аналитический)Выберем начало оси x в точке A
- 20. 2 способ (графический)Отложим в масштабе по оси
- 21. Первое тело нагонит второе через 30 с.
- 22. Два велосипедиста едут навстречу друг другу. Один,
- 23. Ямайский бегун Усейн Болт по прозвищу «Молния»
- 24. Слайд 24
- 25. Источником составления уравнений в задачах на движение
- 26. 3) Если объекты прошли одинаковое расстояние, то
- 27. Два пешехода одновременно вышли навстречу друг другу
- 28. удобно принять за единицу все расстояниеv1 = 1/x,
- 29. Из пункта А в пункт В выехал
- 30. Пусть АВ = s км, v км/ч
- 31. Пешеход вышел из пункта А в пункт
- 32. Используя подобие треугольников AOL и KOM, а
- 33. Из двух городов навстречу друг другу одновременно
- 34. Аналогично предыдущей задаче, необходимо использовать подобие треугольников.Имеем:t/16
Графическое решение задач
Слайд 10По рисунку составьте уравнение зависимости координаты тела от времени х(t)
а=2м/с²
υₒ=3м/с
x,м
2
x,м
2
x = 2 + 3t + t²
Слайд 11
Найдите координату тела через 2,5с
х = 2 + 3·2,5 + 2,5²
= 15,75 м
А как будет выглядеть уравнение зависимости V(t)?
V=Vₒ+at
V=3+2t
Постройте график уравнения
А как будет выглядеть уравнение зависимости V(t)?
V=Vₒ+at
V=3+2t
Постройте график уравнения
Слайд 14Задание 6. Пользуясь графиками, изображенными на рисунке, определите перемещение каждого тела через
4 с. Запишите формулу скорости для каждого движения.
График I.
V0 = 0;
Для любой точки:
a = 1, 25 м/с².
Движение равноускоренное,
v=1,25t;
S= 0,625t²
При t= 4 c →
S = 0,625 • 4² = 10 м; S = 10м.
Слайд 15
График II.
V0 = 2 м/с;
a = 0,75 м/с².
Движение равноускоренное с начальной скоростью:
v
= 2 + 0,75t; S = 2t + 0,375t²;
при t = 4 c → S = 2 • 4 + 0,375 • 4² = 14 м; S = 14 м
при t = 4 c → S = 2 • 4 + 0,375 • 4² = 14 м; S = 14 м
Слайд 16
График III.
V0 = v = 3 м/с;
a = 0.
Движение равномерное:
S
= vt;
S = 3t.
При t = 4 c → S = 3 • 4 = 12 м; S = 12 м.
S = 3t.
При t = 4 c → S = 3 • 4 = 12 м; S = 12 м.
Слайд 17
График IV.
V0 = 7 м/с;
a = - 1,2 м/с.
Движение равнозамедленное:
v = 7
– 1,2t;
S = 7t – 0,6t².
При t = 4 c →
S = 7 • 4 – 0,6 • 4² = 18,4 м.
S = 18,4 м.
S = 7t – 0,6t².
При t = 4 c →
S = 7 • 4 – 0,6 • 4² = 18,4 м.
S = 18,4 м.
Слайд 18
Задача.
Из двух точек А и В, расположенных на расстоянии 90 м
друг от друга, одновременно в одном направлении начали движение два тела. Тело, движущееся из точки А, имело скорость 5 м/с, а тело, движущееся из точки B, - скорость 2 м/с. Через какое время первое тело нагонит второе? Какое перемещение совершит каждое тело?
Слайд 19
1 способ (аналитический)
Выберем начало оси x в точке A и направим её по
движению тел.
Тогда уравнение движения тел таковы:
X1 = v1t, x01 = 0, - начальная координата первого тела.
X2 = x02 +v2t;
X1 и x2 - координаты первого и второго тела. Для точки C, в которой первое тело нагонит второе, x1 = x2, t = t1.Тогда с учётом x1 и x2 получим:
V1t1 = x02 + v2t1,
где t1 - время движения тел до точки встречи С. Из этого уравнения находим время движения тел:
t1= ;
Проверим размерность: t1 = [ = с ]
t 1 = = 30c.
Найдём перемещения тел:
S1 = x1 – x01 = v1t1; S1 = 5 • 30 = 150 м
S2 =x2 - x02 = v2t1; S2 = 2•30 = 60 м
Тогда уравнение движения тел таковы:
X1 = v1t, x01 = 0, - начальная координата первого тела.
X2 = x02 +v2t;
X1 и x2 - координаты первого и второго тела. Для точки C, в которой первое тело нагонит второе, x1 = x2, t = t1.Тогда с учётом x1 и x2 получим:
V1t1 = x02 + v2t1,
где t1 - время движения тел до точки встречи С. Из этого уравнения находим время движения тел:
t1= ;
Проверим размерность: t1 = [ = с ]
t 1 = = 30c.
Найдём перемещения тел:
S1 = x1 – x01 = v1t1; S1 = 5 • 30 = 150 м
S2 =x2 - x02 = v2t1; S2 = 2•30 = 60 м
Слайд 20
2 способ (графический)
Отложим в масштабе по оси абсцисс время t движения, а по
оси ординат – значения координаты x. Запишем уравнения движения тел с учётом условия задачи:
X1 =v1t; x2 = x02 + v2t
X1= 5t; x2 = 90 + 2t.
X1 =v1t; x2 = x02 + v2t
X1= 5t; x2 = 90 + 2t.
Слайд 21
Первое тело нагонит второе через 30 с. Перемещения тел соответственно равны.
S1x = x01=
150 м;
S2x = x2 – x02 = 150 – 90 = 60 м.
Ответ: S1 = 150 м; S2 = 60 м; t1 = 30 c.
S2x = x2 – x02 = 150 – 90 = 60 м.
Ответ: S1 = 150 м; S2 = 60 м; t1 = 30 c.
Слайд 22
Два велосипедиста едут навстречу друг другу. Один, имея скорость 18 км/ч,
движется равнозамедленно с ускорением 20 см/с², другой, имея скорость 5,4 км/ч, движется равноускоренно с ускорением 0,2 м/с². Через какое время велосипедисты встретятся и какое перемещение совершит каждый из них до встречи, если расстояние между ними в начальный момент времени 130 м ?
Ответ: S1 = 60 м; S2 = 70 м; t1 = 20 c.
Ответ: S1 = 60 м; S2 = 70 м; t1 = 20 c.
Слайд 23
Ямайский бегун Усейн Болт по прозвищу «Молния» считается самым быстрым спринтером
на Земле. Он пробегает 200 метров за 17,95 секунд, из которых 3 секунды он потратил на разгон. Остальное время он двигался равномерно. Чему равна его рекордная скорость равномерного движения?
Слайд 25
Источником составления уравнений в задачах на движение служат следующие соображения:
1) Объекты,
начавшие движение навстречу друг другу одновременно, движутся до момента встречи одинаковое время. Время, через которое они встретятся, находят по формуле
t = s/(v1 + v2) (*).
2) Если одно тело догоняет другое, то время, через которое первый догонит второго, вычисляется по формуле
t = s/(v1 – v2) (**).
t = s/(v1 + v2) (*).
2) Если одно тело догоняет другое, то время, через которое первый догонит второго, вычисляется по формуле
t = s/(v1 – v2) (**).
Слайд 26
3) Если объекты прошли одинаковое расстояние, то величину этого расстояния удобно
принять за общее неизвестное задачи.
4) Если при одновременном движении двух объектов по окружности из одной точки, один из них догоняет в первый раз другого, то разность пройденных ими к этому моменту расстояний равна длине окружности
c = 2πR.
5) Для времени новой встречи при движении в противоположных направлениях получим формулу (*), если в одном направлении – то формулу (**).
6) При движении по течению реки скорость объекта равна сумме скоростей в стоячей воде и скорости течения. При движении против течения скорость движения есть разность этих скоростей.
4) Если при одновременном движении двух объектов по окружности из одной точки, один из них догоняет в первый раз другого, то разность пройденных ими к этому моменту расстояний равна длине окружности
c = 2πR.
5) Для времени новой встречи при движении в противоположных направлениях получим формулу (*), если в одном направлении – то формулу (**).
6) При движении по течению реки скорость объекта равна сумме скоростей в стоячей воде и скорости течения. При движении против течения скорость движения есть разность этих скоростей.
Слайд 27
Два пешехода одновременно вышли навстречу друг другу и через 3 часа
20 минут встретились. Сколько времени понадобилось каждому пешеходу, чтобы пройти все расстояние, если известно, что первый пришел в пункт, из которого вышел второй, на 5 часов позже, чем второй пришел в пункт, откуда вышел первый?
Слайд 28удобно принять за единицу все расстояние
v1 = 1/x, а второго – v2 =
1/y, где x часов – время в пути первого, а y – время в пути второго пешеходов.
Условия задачи позволяют составить систему уравнений:
{3⅓ · 1/x + 3⅓ · 1/y = 1, {x – y = 5.
Ответ: 10 часов и 5 часов.
Условия задачи позволяют составить систему уравнений:
{3⅓ · 1/x + 3⅓ · 1/y = 1, {x – y = 5.
Ответ: 10 часов и 5 часов.
Слайд 29
Из пункта А в пункт В выехал велосипедист. Через 3 часа
навстречу ему из пункта В выехал мотоциклист, со скоростью в 3 раза большей, чем скорость велосипедиста. Встреча велосипедиста и мотоциклиста происходит посередине, между пунктами А и В. В случае выезда мотоциклиста позже велосипедиста на 2 часа, их встреча произошла бы на 15 километров ближе а пункту А. Найти расстояние АВ.
Слайд 30
Пусть АВ = s км, v км/ч – скорость велосипедиста, 3v
км/ч – скорость мотоциклиста.
t1 = 0,5 s/v часов – время до встречи велосипедиста,
t2 = 0,5 s/3v часов – время до встречи мотоциклиста.
По условию t1 – t2 = 3, значит 0,5 s/v – 0,5s / 3v = 3, откуда s = 9v.
Если бы мотоциклист выехал на 2 часа позже велосипедиста, то они встретились бы в точке F.
AF = 0,5s – 15, BF = 0,5s + 15.
Составим уравнение: (0,5s – 15)/v – (0,5s + 15)/3v = 2, откуда s – 60 = 6v.
Получим систему уравнений:
{s = 9v, {s = 60 + 6v.
Имеем:
{v = 20, {s = 180.
Ответ: v = 20 км/ч, s = 180 км.
t1 = 0,5 s/v часов – время до встречи велосипедиста,
t2 = 0,5 s/3v часов – время до встречи мотоциклиста.
По условию t1 – t2 = 3, значит 0,5 s/v – 0,5s / 3v = 3, откуда s = 9v.
Если бы мотоциклист выехал на 2 часа позже велосипедиста, то они встретились бы в точке F.
AF = 0,5s – 15, BF = 0,5s + 15.
Составим уравнение: (0,5s – 15)/v – (0,5s + 15)/3v = 2, откуда s – 60 = 6v.
Получим систему уравнений:
{s = 9v, {s = 60 + 6v.
Имеем:
{v = 20, {s = 180.
Ответ: v = 20 км/ч, s = 180 км.
Слайд 31
Пешеход вышел из пункта А в пункт В. Вслед за ним
из пункта А выехал велосипедист, но с задержкой в 2 часа. Еще через 30 минут по направлению к пункту В выехал мотоциклист. Пешеход, велосипедист и мотоциклист двигались в пункт В без остановок и равномерно. Через некоторое время после того, как выехал мотоциклист, оказалось, что к этому моменту все трое преодолели одинаковую часть пути от А до В. На сколько минут раньше пешехода велосипедист прибыл в пункт В, если мотоциклист прибыл в пункт В на 1 час раньше пешехода?
Слайд 32
Используя подобие треугольников AOL и KOM, а так же треугольников AOP
и KON можно составить пропорцию:
x/1 = 2/2,5;
x = 4/5 ч = 48 минут.
Ответ: 48 минут.
x/1 = 2/2,5;
x = 4/5 ч = 48 минут.
Ответ: 48 минут.
Слайд 33
Из двух городов навстречу друг другу одновременно вышли два посыльных. После
встречи один из них был в пути еще 16 часов, а второй – 9 часов. Определить, сколько времени был в пути каждый посыльный.
Слайд 34
Аналогично предыдущей задаче, необходимо использовать подобие треугольников.
Имеем:
t/16 = 9/t;
t2 = 144;
t =
12.
Значит, 12 + 16 = 28 (часов) – был в пути первый, 12 + 9 = 21 (час) – был в пути второй.
Ответ: 21 час и 28 часов.
Значит, 12 + 16 = 28 (часов) – был в пути первый, 12 + 9 = 21 (час) – был в пути второй.
Ответ: 21 час и 28 часов.