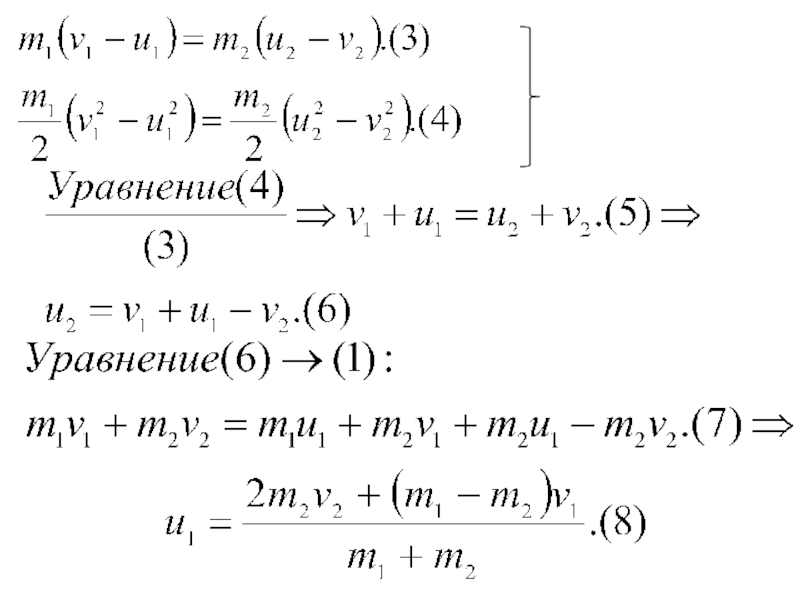- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Олимпиада по физике 8 класс
Содержание
- 1. Олимпиада по физике 8 класс
- 2. Потенциальное поле – поле консервативных сил.полная механическая
- 3. Полная механическая энергия материальной точки (тела, частицы),
- 4. Потенциальные кривыеОдномерное движение тела (материальной точки). В
- 5. Рассмотрим консервативную систему, т.е. систему, в которой
- 6. Слайд 6
- 7. • Области (ab); (cd): частица находится в
- 8. Закон сохранения энергии в механикеРассмотрим механическую систему,
- 9. Второй закон Ньютона для i точки: Под действием силы точка за время dt совершает перемещение dri:
- 10. Суммируя по всем точкам, получаем:При переходе системы
- 11. Если внешние неконсервативные силы отсутствуют, т.е. Полная
- 12. ● Замкнутая система – частный случай.В этом
- 13. Наряду с консервативными силами в системе могут
- 14. Закон сохранения энергии в механике является частным
- 15. Применение законов сохранения импульса и энергии для
- 16. Сила взаимодействия при ударе тел велика следовательно,
- 17. Если деформация упругая, то тело стремится принять
- 18. Во время удара происходит перераспределение энергии между
- 19. Абсолютно упругий удар – удар, при котором
- 20. Слайд 20
- 21. Слайд 21
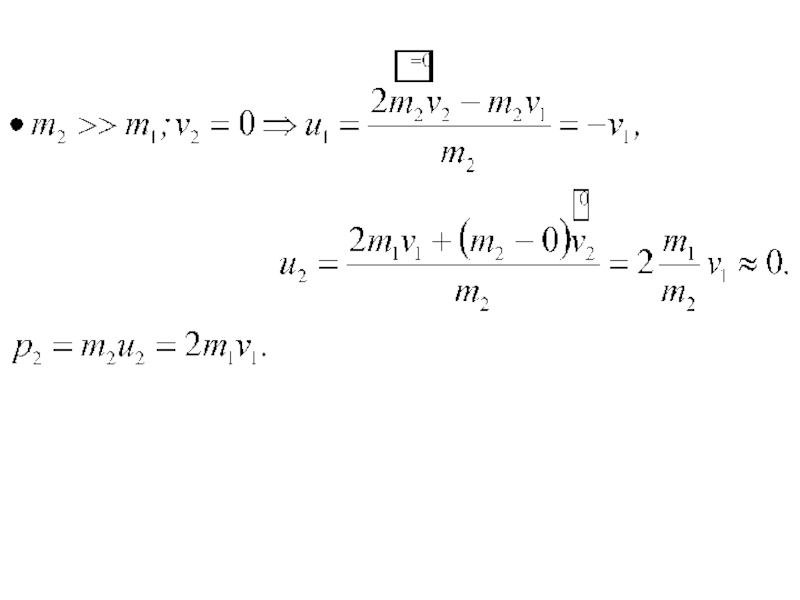
- 22. Слайд 22
- 23. При одинаковых массах происходит обмен скоростями.
- 24. Абсолютно неупругий удар – удар, при котором
- 25. ● НаковальняВся энергия переходит в теплоту или деформацию.
- 26. ● Удар молотка по гвоздю.Вся энергия переходит в механическую энергию.
Слайд 1Закон сохранения энергии в механике
Закон сохранения энергии материальной точки,
находящейся в
Слайд 2Потенциальное поле – поле консервативных сил.
полная механическая
энергия системы.
– совершается работа,
– связь силы и
потенциальной энергии
Слайд 3Полная механическая энергия материальной точки (тела, частицы), находящейся в потенциальном поле
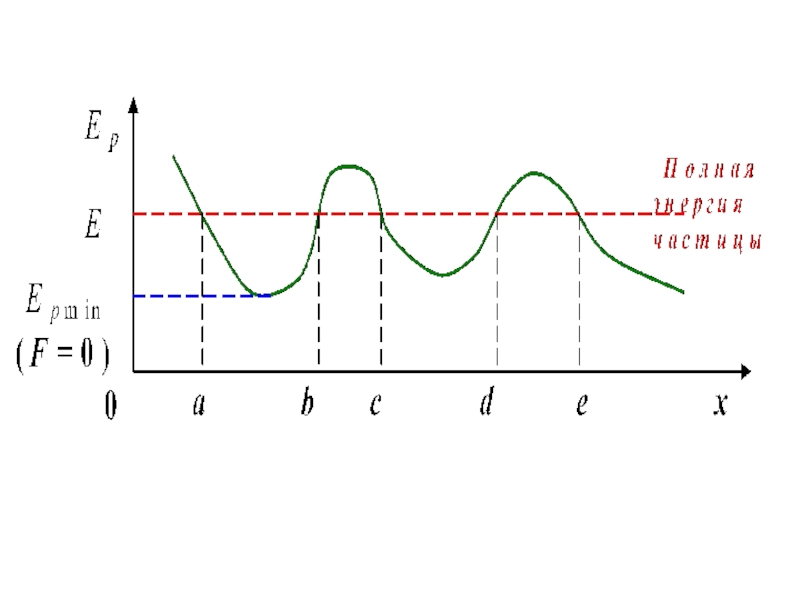
Слайд 4Потенциальные кривые
Одномерное движение тела (материальной точки). В этом случае Ер является
График зависимости Ер от некоторого аргумента называется потенциальной кривой.
Анализ потенциальных кривых определяет характер движения тел.
Слайд 5
Рассмотрим консервативную систему, т.е.
систему, в которой превращение механической
энергии в
В ней действует закон сохранения энергии:
Кинетическая энергия не может быть
отрицательной, потому
Для частиц (материальных точек)
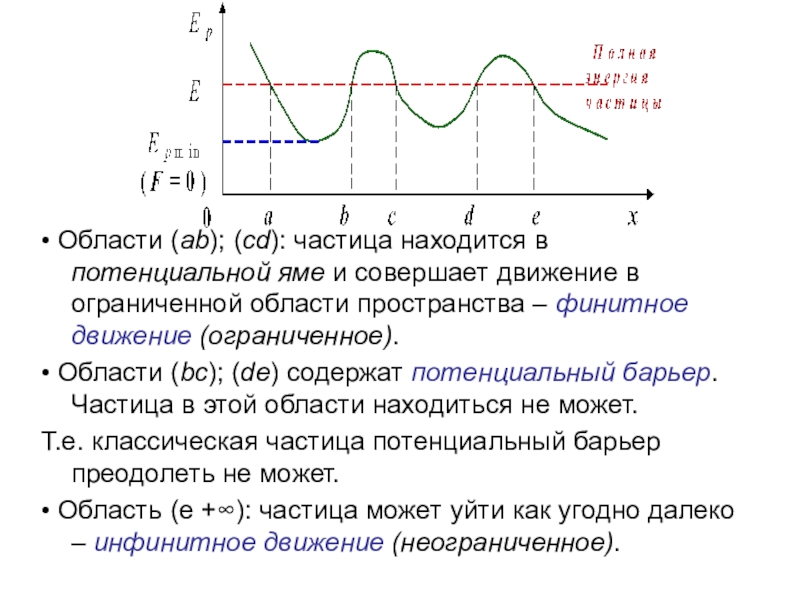
Слайд 7• Области (ab); (cd): частица находится в потенциальной яме и совершает
• Области (bc); (de) содержат потенциальный барьер. Частица в этой области находиться не может.
Т.е. классическая частица потенциальный барьер преодолеть не может.
• Область (е +∞): частица может уйти как угодно далеко – инфинитное движение (неограниченное).
Слайд 8Закон сохранения энергии в механике
Рассмотрим механическую систему, состоящую из n материальных
– внутренние консервативные силы.
– внешние консервативные силы.
– внешние неконсервативные силы.
Слайд 9Второй закон Ньютона для i точки:
Под действием силы точка за
Слайд 10Суммируя по всем точкам, получаем:
При переходе системы из одного состояния в
работа, совершаемая внешними
неконсервативными силами.
Слайд 11Если внешние неконсервативные силы отсутствуют, т.е.
Полная механическая энергия консервативной системы
Консервативной системой называется механическая система, внутренние силы которой консервативны, а внешние силы – консервативны и стационарны.
Закон сохранения механической энергии связан с однородностью времени, т.е. физические законы инвариантны относительно начала отсчета времени.
Слайд 12● Замкнутая система – частный случай.
В этом случае внешние силы не
– полная механическая энергия системы. Происходит превращение Ep → Ек, и обратно Ек → Ep .
Слайд 13Наряду с консервативными силами в системе могут существовать неконсервативные силы (диссипативные,
Слайд 14Закон сохранения энергии в механике является частным случаем фундаментального (всеобщего) закона
сумма всех видов энергии в замкнутой системе постоянна
Слайд 15Применение законов сохранения импульса и энергии для анализа упругого и неупругого
Удар – кратковременное взаимодействие двух или более тел.
Центральный удар (двух шаров) – удар, при котором движение происходит по прямой, соединяющей центры тел.
Слайд 16Сила взаимодействия при ударе тел велика
следовательно, внешними силами, действующими на
Тело во время удара претерпевает деформацию. Кинетическая энергия во время удара переходит в энергию деформации.
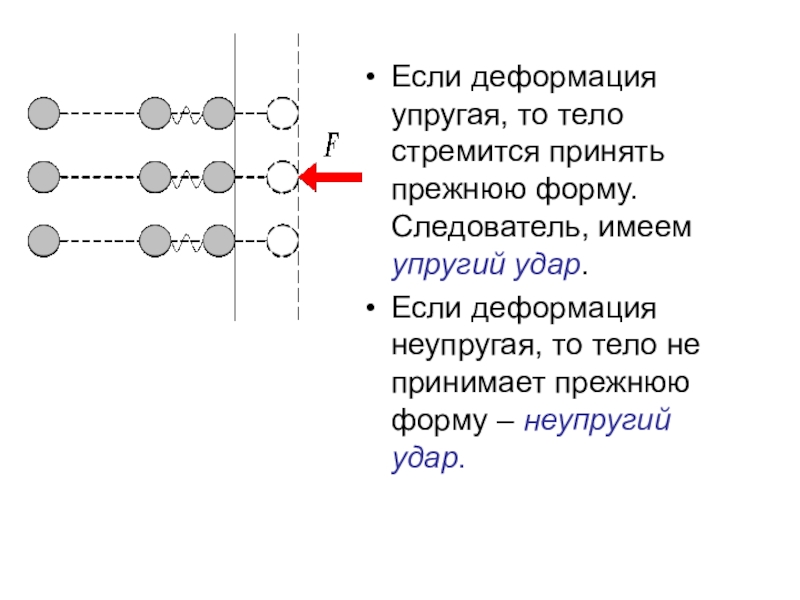
Слайд 17Если деформация упругая, то тело стремится принять прежнюю форму. Следователь, имеем
Если деформация неупругая, то тело не принимает прежнюю форму – неупругий удар.
Слайд 18Во время удара происходит перераспределение энергии между соударяющимися телами.
В общем
Коэффициент восстановления – отношение нормальных составляющих относительной скорости после удара un и до удара vn:
ε = 1 – абсолютно упругий удар.
ε = 0 – абсолютно неупругий удар.
Слайд 19Абсолютно упругий удар – удар, при котором внутренняя энергия соударяющихся тел
Закон сохранения импульса:
Закон сохранения энергии:
Слайд 24Абсолютно неупругий удар – удар, при котором полная механическая энергия соударяющихся
При абсолютно неупругом ударе тела после удара двигаются с одинаковой скоростью.