- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Мастер - класс по развитию мыслительной деятельности с детьми ЗПР
Содержание
- 1. Презентация по математике Мастер - класс по развитию мыслительной деятельности с детьми ЗПР
- 2. Известно, что математика
- 3. Психолого-педагогические исследования, а также практика обучения детей
- 4. Слайд 4
- 5. Изучение
- 6. На
- 7. Например, изучение равнобедренного треугольника можно
- 8. Какой треугольник «лишний»?1423
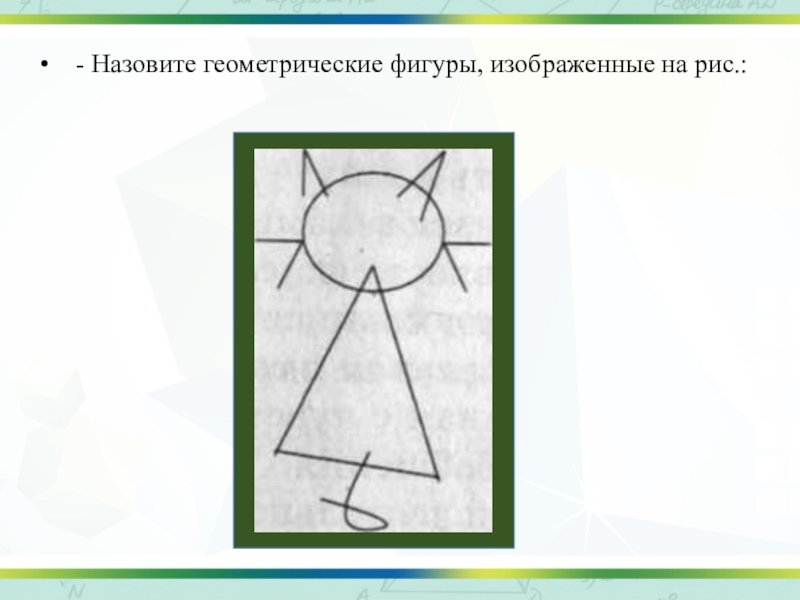
- 9. - Назовите геометрические фигуры, изображенные на рис.:
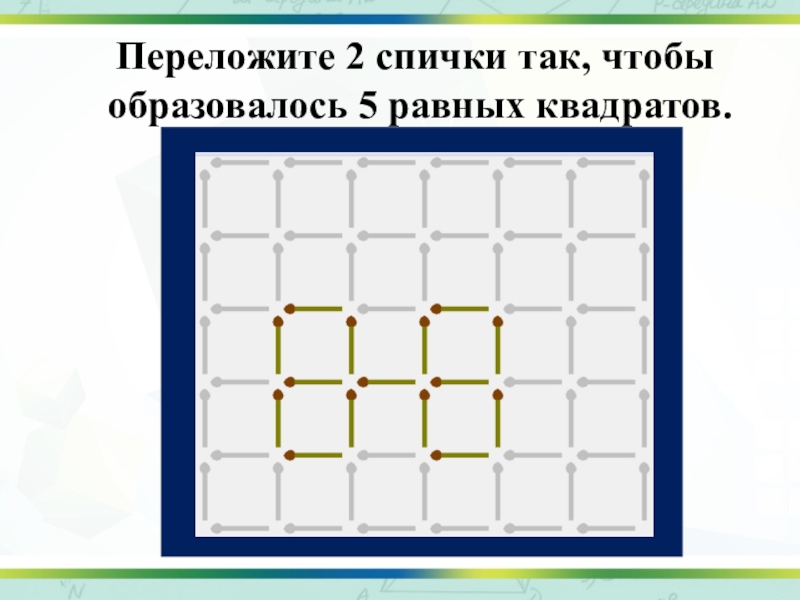
- 10. Переложите
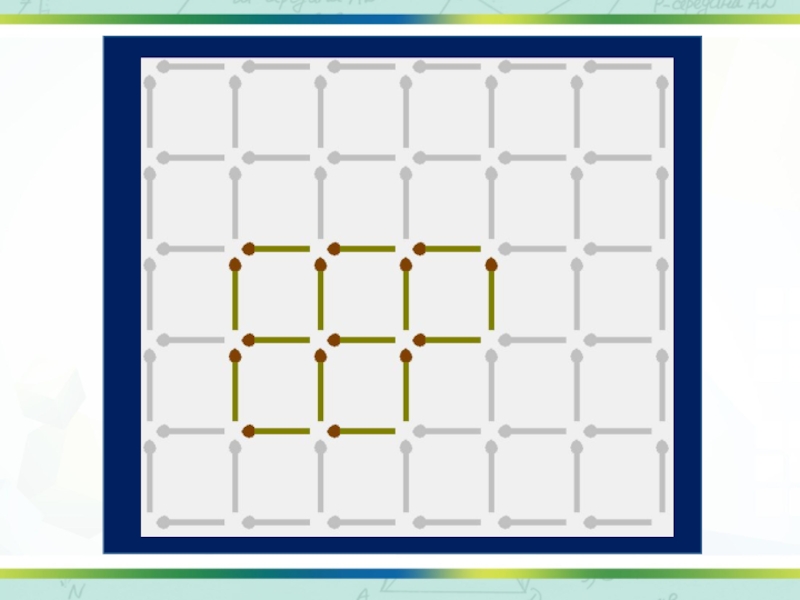
- 11. Слайд 11
- 12. Разделите круглый сыр тремя разрезами на 8 одинаковых частей.
- 13. . 2) группе заданий, направленных на развитие
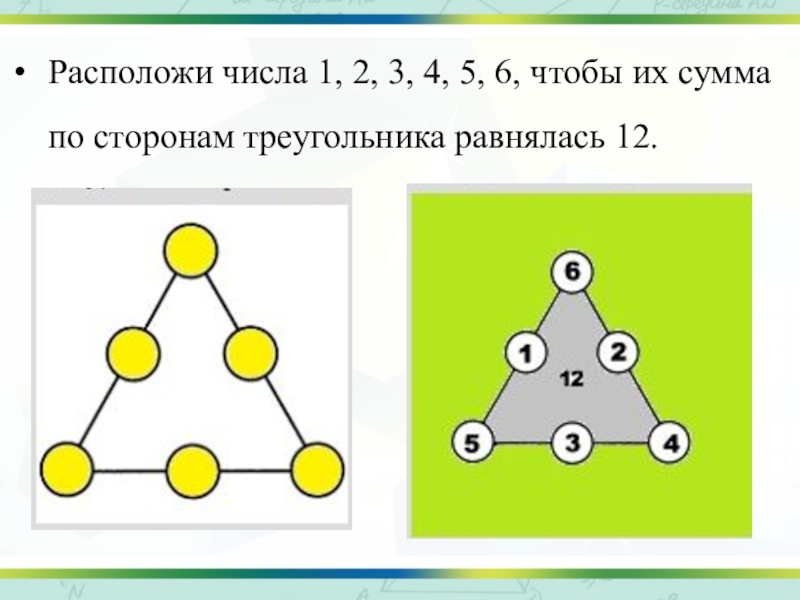
- 14. Расположи числа 1, 2, 3, 4, 5, 6, чтобы их сумма по сторонам треугольника равнялась 12.
- 15. Расставьте в записискобки так, чтобы значение получившегося
- 16. Найди «сбежавшие» числа: 56 - …
- 17. ПОМОГИТЕ ! У меня не
- 18. Слайд 18
- 19. 3) группе заданий, направленных на формирование у
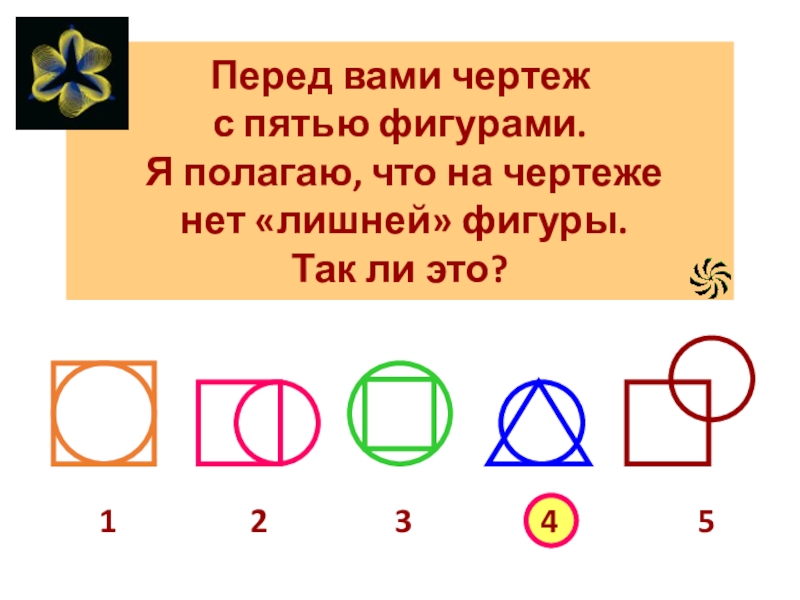
- 20. Перед вами чертеж с пятью фигурами. Я
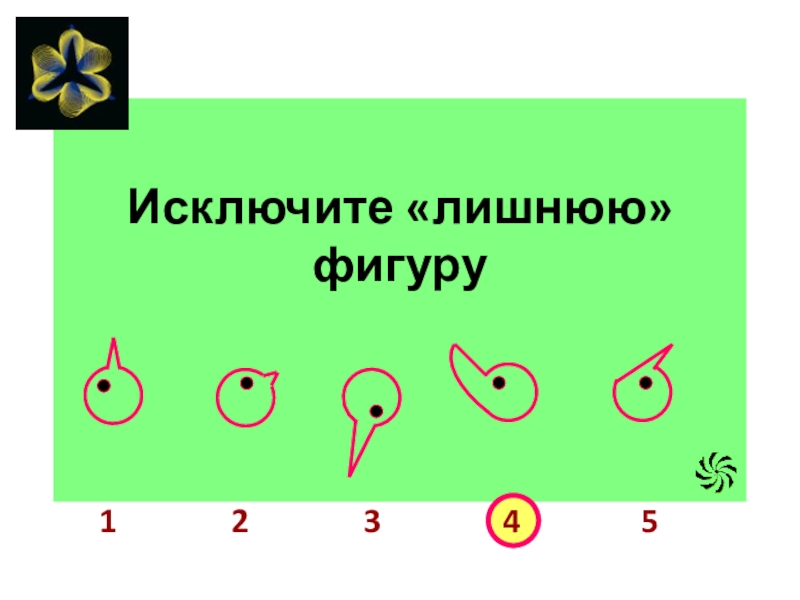
- 21. Исключите «лишнюю» фигуру12345
- 22. Слайд 22
- 23. Сколько треугольников?12
- 24. Слайд 24
- 25. Авгкспзрфдесятичнаясвщтрадробьрсмцкбгфмнщсложениепрививкасонвычитаниетрросразрядснегопрямаявеникптомчкатронспрзнаменательсвфмиокрпиктотрубакримонеёжбнрпсчислитель
- 26. 4) группе заданий, представленных задачами-шутками, считалочками, ребусами.
- 27. Летела стая гусей. Один гусь впереди и
- 28. Женщина обращается к кому-то из вашего класса
- 29. Волк и лиса соревновались в беге. Кто
- 30. ВОСТОК ТОЧКАТРЕУГОЛЬНИК
- 31. Слайд 31
- 32. Обратная связь (отображения ответов с помощью карточек)
- 33. Любое открытие, пусть самое маленькое,
- 34. У детей с ЗПР наблюдается отставание
- 35. Мастер-класс мне …понравилсябыло скучноне понравился
- 36. Удачи в стране знаний!
- 37. Спасибо за ВНИМАНИЕ!
- 38. Интернет-Ресурсыhttp://pedsovet.su/load/412 шаблон презентации http://articlekz.com/article/5790 Развитие мыслительной деятельности
- 39. Слайд 39
Слайд 1 Мастер-класс
по развитию мыслительной деятельности детей с ЗПР на
в 2 – 4 классах.
Учитель начальных классов Пешехонова М. А.
Слайд 2 Известно, что математика как учебный предмет требует
ребенка наличия определенных способностей:
умения анализировать и обобщать материал;
мыслить отвлеченно, абстрактными категориями;
гибкости мышления;
наличия специфической математической памяти.
Указанные способности, необходимые для успешного овладения
математическими знаниями, у детей с ОВЗ развиты недостаточно.
Слайд 3Психолого-педагогические исследования, а также практика обучения детей с ЗПР свидетельствуют о
Слайд 4 Показано, что специфическое отставание
недостаточное развитие способности к обобщению,
ригидность мыслительных действий,
недостаточное развитие способности к логическому мышлению.
Слайд 5 Изучение математики должно быть направлено
Занимательный математический материал, составленный на основе законов мышления, является одним из дидактических средств, способствующих формированию математических представлений детей и развитию приемов умственной деятельности.
Слайд 6 На уроках математики необходимо большое
1) упражнениям по преобразованию геометрических фигур, направленным на уточнение знаний о геометрических фигурах и их свойствах, на развитие сенсорных и мыслительных способностей, усвоение способов преобразования соединения. С этой целью используются игры на составление фигур-силуэтов, геометрических фигур, предназначенные для развития у детей пространственного воображения, логического и интуитивного мышления. Они вызывают у учащихся с задержкой психического развития интерес к конечному результату, желание решить задачу самостоятельно, проявляя настойчивость, смекалку, сообразительность. Игры такого типа совершенствуют наглядно-образное мышление школьников, создают условия для развития логических компонентов мышления.
Слайд 7 Например, изучение равнобедренного треугольника можно предварить следующим упражнением:
- Постройте
Выполнив данное упражнение, обращаем внимание на то, что в каждом из полученных треугольников две стороны равны, что дает возможность ввести понятие равнобедренного треугольника.
Слайд 13. 2) группе заданий, направленных на развитие логического мышления, умения размышлять,
Слайд 15Расставьте в записи
скобки так, чтобы значение
получившегося выражения
было бы равно
( ) ( )
Слайд 16Найди «сбежавшие» числа:
56 - … =
15 + … = 36
… + 24 = 67
… - 51 = 13
54 : … = 6
9 × … =72
64
43
21
24
9
42
7
6
8
23
Слайд 17 ПОМОГИТЕ !
У меня не
получается.
Найдите ошибку!
- 68_
1348
- 68_
1 280
1230
15
1230
- 15
1215
Слайд 193) группе заданий, направленных на формирование у учащихся мыслительных процессов: анализ,
Слайд 20Перед вами чертеж
с пятью фигурами.
Я полагаю, что на чертеже
Так ли это?
1
2
3
4
5
Слайд 24 «Потерянные» слова.
Незнайка растерял не только запятые, но и слова. Ваша задача среди букв найти слова - математические термины. Смотреть нужно по строчкам.
Авгкспзрфдесятичнаясвщтрадробьрсмцкбгфмнщсложениеприв
ивкасонвычитаниетрросразрядснегопрямаявеникптомчкатронс
прзнаменательсвфмиокрпиктотрубакримонеёжбнрпсчислитель
Слайд 25Авгкспзрфдесятичнаясвщтрадробьрсмцкбгфмнщсложениеприв
ивкасонвычитаниетрросразрядснегопрямаявеникптомчкатронс
прзнаменательсвфмиокрпиктотрубакримонеёжбнрпсчислитель
Слайд 264) группе заданий, представленных задачами-шутками, считалочками, ребусами. В задачах-шутках имеются числовые
Слайд 27Летела стая гусей.
Один гусь впереди и два позади.
Один гусь позади
один между двумя
и три в ряд.
Сколько их было?
Три, друг за другом.
Слайд 28Женщина обращается к кому-то
из вашего класса и говорит:
«Я тебе
Что это значит?
Она обращается к девочке.
Слайд 29Волк и лиса
соревновались в беге.
Кто какое место занял,
Если известно,
волк был одним из первых,
а лиса была предпоследней?
Лиса - 1 место,
волк - 2 место.
Слайд 31
с детьми с ОВЗ имеют ряд преимуществ:
1. Дают возможность охватить большой объём материала за короткий промежуток времени.
2. Позволяют по реакции класса в тот или иной мере судить об усвоении материала, готовить к изучению нового, помогают выявить ошибки.
3. Дисциплинируют учащихся, помогают настроиться на работу в начале урока.
4. В середине и в конце урока служат переключением внимания, интересной, своеобразной разрядкой после напряжения и усталости, вызванной письменной работой. При этом обеспечивается самостоятельность выполнения заданий.
5. Больше учащихся получают возможность ответить, проверить правильность решений.
6. Каждый ученик, по мере своих возможностей, может ответить на тот или иной вопрос или задание.
Слайд 33 Любое открытие, пусть самое маленькое, сделанное при решении даже
Слайд 34 У детей с ЗПР наблюдается отставание в развитии всех форм
Использование разнообразного занимательного математического материала создает благоприятные условия для развития мыслительной деятельности школьников с задержкой психического развития, а именно развивает математическое мышление, активизирует познавательную деятельность, способствует повышению интереса и положительной мотивации к математике.
Слайд 38Интернет-Ресурсы
http://pedsovet.su/load/412 шаблон презентации
http://articlekz.com/article/5790 Развитие мыслительной деятельности детей младшего школьного возраста
3) www.myshared.ru презентации онлайн
4) http://garnett.ru/10-klass/formirovanie-prostranstvennykh-i-geometricheskikh-predstavlenii-u-uchashchikhsia-spetcialnoi-ko/ Формирование пространственных и геометрических представлений у учащихся специальной (коррекционной) общеобразовательной школы VIII вида.
5) http://vsemzagadki.narod.ru/magia_chisel/chislovye_treugolniki.html Магия чисел
Новикова Е. Н. Использование элементов технологии самосовершенствования личности на уроках математики в классах коррекционно – компенсирующего обучения
Тарасова В. В. Устный счёт на уроках математики
http://miranimashek.com/photo/animacija_animashki/63-0-11619