- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Длина окружности (3 урок)
Содержание
- 1. Презентация по математике Длина окружности (3 урок)
- 2. Математический диктант 1)Если стороны многоугольника являются
- 3. Представим окружность из тонкой нити.
- 4. Вывод формулы длины окружности
- 5. O1Свойство длины окружности.Отношение длины окружности к её
- 6. По свойству пропорцииДоказательство:1) Впишем в каждую окружность
- 7. Число «пи».Число π – бесконечная десятичная дробь.π
- 8. Вывод формулы длины окружности
- 9. Вопросы для повторения.Сформулируйте основное свойство длины окружности.
- 10. Слайд 10
- 11. .Ответы.
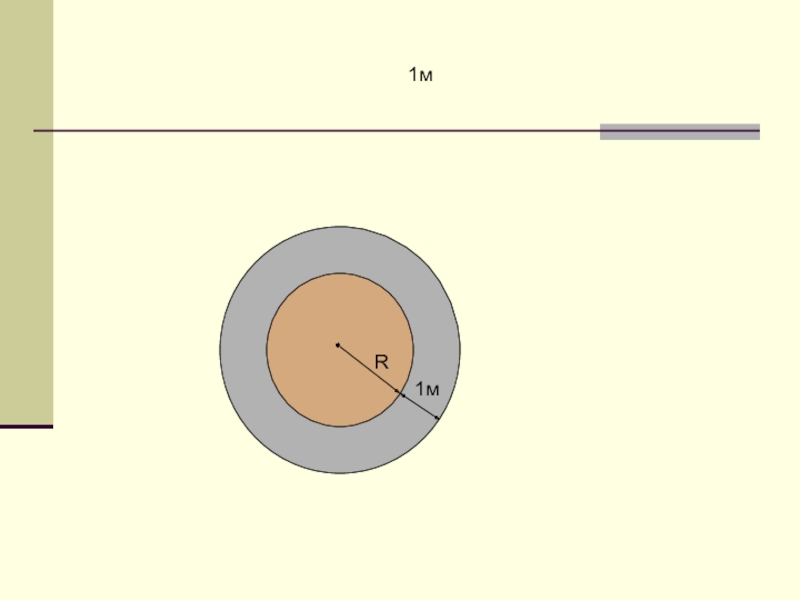
- 12. Радиус окружности увеличился на 1 м. На сколько при этом увеличилась длина окружности?
- 13. 1м1мR1м
- 14. Закрепление изученного материала (решение задач)№ 1104(а). Найти
- 15. № 1104(а). Найти длину окружности описанной около
- 16. R
- 17. № 1104 (в). Найти длину окружности
Слайд 2Математический диктант
1)Если стороны многоугольника являются хор-дами, то окружность называется…
2)Если
3) Если сторона правильного многоугольника
стягивает дугу окружности, равную 36 градусам, то многоугольник имеет …сторон.
4)Сторона правильного многоугольника, вписан-ного в окружность радиуса R, вычисляется по формуле …
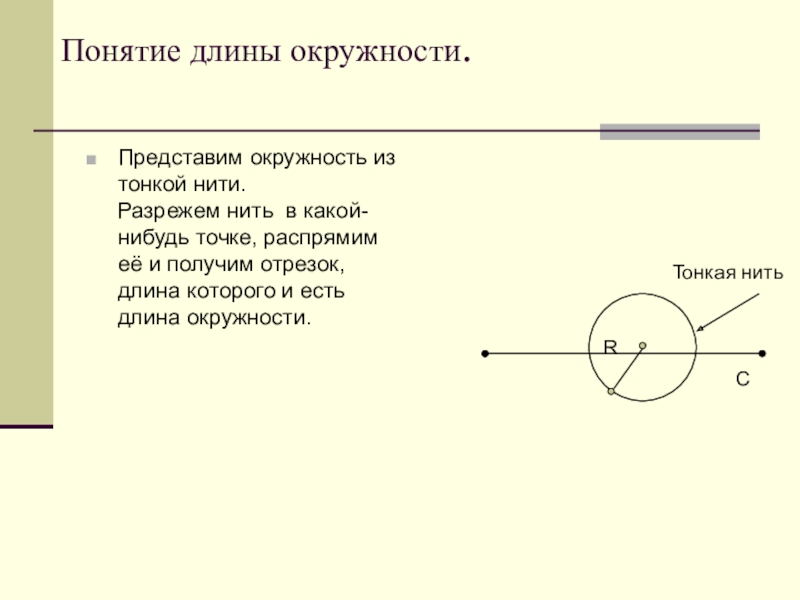
Слайд 3Представим окружность из тонкой нити. Разрежем
Понятие длины окружности.
Тонкая нить
С
Слайд 4
Вывод формулы длины окружности
Длина окружности –
Периметр любого вписанного в
окружность многоугольника является
приближённым значением
длины окружности.
При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к окружности
Слайд 5O1
Свойство длины окружности.
Отношение длины окружности к её диаметру есть одно и
Дано:
Окр (О1;R1) ,Oкр(O2;R2),
C1 – длина Oкр(O1; R1),
C2 – длина Oкр(O2; R2).
Доказать:
O2
Слайд 6По свойству пропорции
Доказательство:
1) Впишем в каждую окружность правильный n-угольник.
Если число сторон
Пусть Р1, Р2 – их периметры;
а аn1, an2 – их стороны.
Тогда P1= n.an1=
Ч.т.д.
P1→C1, P2→C2 тогда
Слайд 7Число «пи».
Число π – бесконечная десятичная дробь.
π – первая буква греческого
Впервые такое обозначение ввел в 1706 году английский математик Джонс. Общепринятым это обозначение стало в 1736 году, после одной из работ Эйлера, великого математика, физика, астронома.
π = 3,141592653589793238462643… (24 знака).
Вычисление как можно большего числа точных цифр числа π с помощью ЭВМ занимает математиков и в настоящее время. Так в 1988 году японский ученый Ясума Канеда вычислил 400 миллионов точных цифр после запятой. Это не только спортивный интерес, но это необходимо и для изучения случайных процессов…В школьном же курсе математики π =3,14.
Слайд 9Вопросы для повторения.
Сформулируйте основное свойство длины окружности. На чем основывается его
Как вычисляется длина окружности по формуле?
Какое число обозначается буквой и чему равно его приближённое значение?
Как изменится длина окружности, если радиус окружности уменьшить (увеличить в) K раз ?
Слайд 14Закрепление изученного материала (решение задач)
№ 1104(а). Найти длину окружности описанной около
(в). Найти длину окружности описанной около равнобедренного треугольника с основанием а и стороной b
Слайд 15
№ 1104(а). Найти длину окружности описанной около правильного треугольника со стороной
Выразите R через а.
Подставьте в формулу длины окружности.
Слайд 16 R
R
H
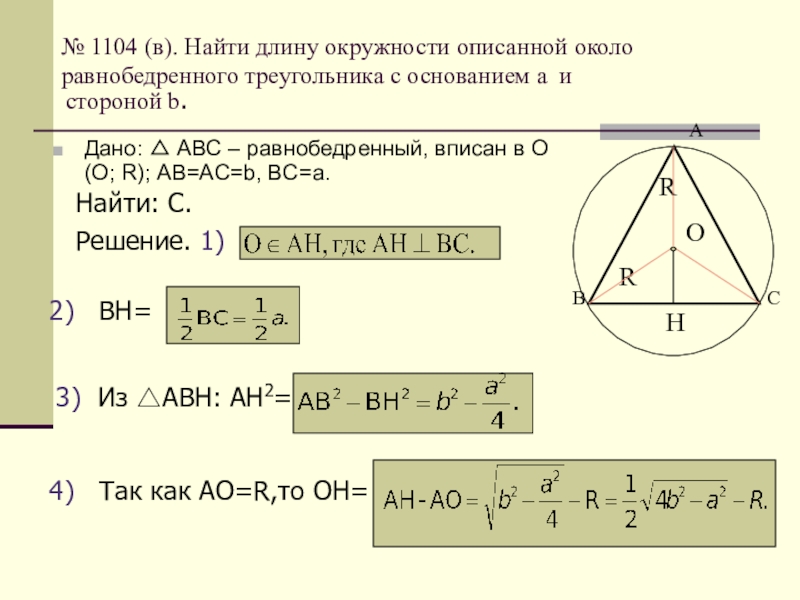
Дано: △ АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a.
№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием а и
А
В
С
ВН=
Из △АВН: АН2=
Так как АО=R,то ОН=
стороной b.
Найти: С.
Решение. 1)
Слайд 17
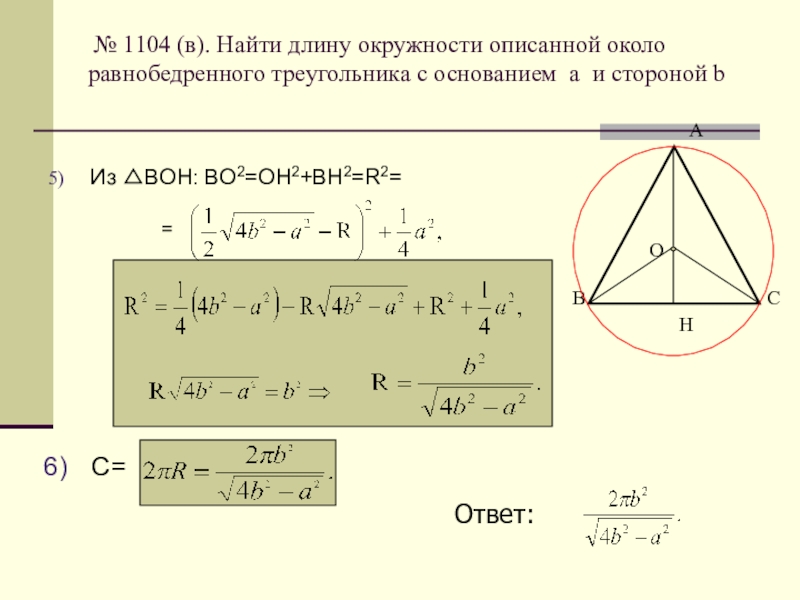
№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника
Из △ВОН: BО2=OH2+BH2=R2=
А
В
С
Н
C=
О
Ответ:
=