- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к выступлению Формирование решать задачи в различных УМК
Содержание
- 1. Презентация к выступлению Формирование решать задачи в различных УМК
- 2. Плохой учитель преподносит истину, хороший –
- 3. УМК «Начальная школа XXI века».
- 4. Мастер делает за 1 ч. 6 деталей,
- 5. Цель: Рассмотреть подходы к формированию
- 6. Введение. Главное достоинство изучения математики состоит
- 7. Работа по формированию умения решать задачи начинается
- 8. На первом этапе параллельно с формированием умения
- 9. По реке катер проплыл _______км, а по
- 10. Решение:12:3=4 (с.)Ответ: 4 слова.Придумай вопрос к задаче,
- 11. В конюшне 18 лошадей. Сколько упряжек получится,
- 12. Решение:1) * 4 =
- 13. Было - ?Взяли – 81 кн. и
- 14. Придумай вопрос к условию задачи, чтобы ее
- 15. Таким образом, в процессе решения задач ребенок
- 16. УМК «Школа 2100»
- 17. Ведущую роль в осознании текста, отношений, поиска
- 18. Найдите задачу1.«У Тани 4 гриба».2.«У Тани 4
- 19. ЗАДАЧАУ Тани 4 гриба, а у Саши
- 20. УСЛОВИЕУ Тани 4 гриба, а у Саши - 2 гриба.
- 21. ВОПРОССколько грибов у Тани и Саши вместе?ВОПРОС
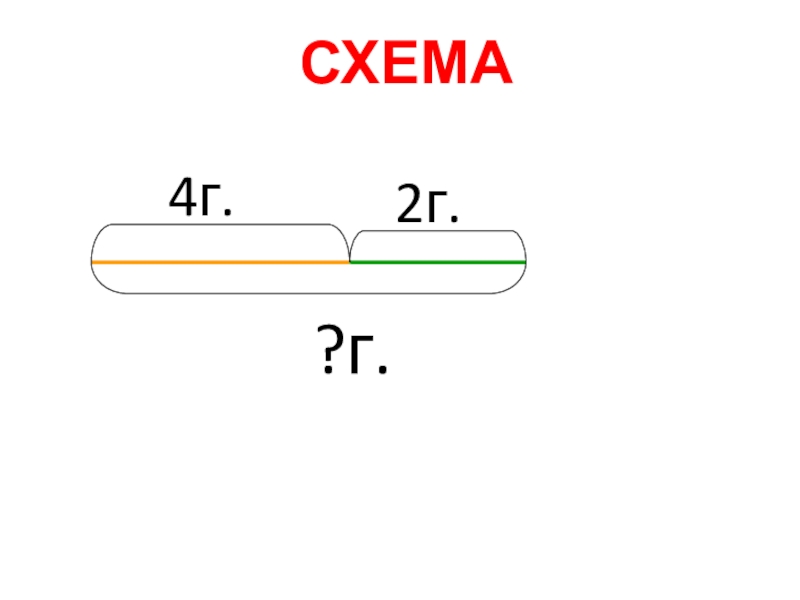
- 22. СХЕМА4г.2г.?г.
- 23. ОТВЕТ 6 грибов
- 24. ЗАПИСЬ ЗАДАЧИТаня -4г. Саша -2г.?г.4+2=6(г.)Ответ: 6 грибов.
- 25. Задание 1.Прочитай текст справа и текст слева.Петя
- 26. Задание 2Какую задачу можно придумать по рисунку
- 27. !Условие и вопрос этой задачи можно записать
- 28. Таким образом, к 3-му,
- 29. УМК «Развивающая система Л. В. Занкова».
- 30. Развивающая система Л.В.
- 31. Структура работы с задачами, которая предлагается в
- 32. Наибольшее внимание в учебниках математики по системе
- 33. В учебниках 1 класса присутствуют специальные задания,
- 34. 11. Придумайте математические рассказы по рисунку.
- 35. 23. Придумайте по рисунку два математических рассказа.
- 36. Рассмотри рисунки ниже. Чем они отличаются от
- 37. 88. Выбери из трёх текстов задачу.а) На ладонь
- 38. Слайд 38
- 39. Задание 58 (ч.2). Придумай математический рассказ к
- 40. Во втором классе начинается овладение одним их
- 41. Работа над задачами осуществляется в трёх основных
- 42. Виды заданий2 класс,ч.2 с.11271 1) Дед Мороз
- 43. Задание №112 (2 кл.). 1) Прочитай тексты
- 44. Большое внимание в программе
- 45. В учебниках различных УМК представлены задачи
- 46. Список используемой литературы Сборник программ к комплекту
- 47. 4. Демидова Т. Е.,
Слайд 2
Плохой учитель преподносит истину, хороший – учит ее находить.
А. Дистервег
Система
Л.В. Занкова
Школа 2100
Школа 21 века
Слайд 4Мастер делает за 1 ч. 6 деталей, а ученик 2 детали.
Способ 1
1. Сколько деталей сделает мастер за 6 ч?
_______________________
2. Сколько деталей сделает ученик за 6 ч?
_______________________
3. Сколько деталей сделают всего?
_______________________
Способ 2
1. Сколько деталей сделают мастер и ученик вместе за 1 ч?
_______________________
2. Сколько деталей сделают мастер и ученик вместе за 6 ч?
_______________________
Слайд 5Цель:
Рассмотреть подходы к формированию общих умений решать задачи
«Начальная школа XXI века»
«Школа 2100».
«Развивающая система Л.В. Занкова»
Слайд 6Введение.
Главное достоинство изучения математики состоит в пристальном внимании к
Система работы с текстовыми задачами позволяет сформировать у каждого ученика полноценное умение решать задачи не за счет «натаскивания» на основе ранней типизации задач и большого числа их, а за счет разнообразной творческой деятельности каждого ученика.
Слайд 7 Работа по формированию умения решать задачи начинается с первых дней обучения
Слайд 8 На первом этапе параллельно с формированием умения пересчитывать предметы начинается подготовка
На втором этапе внимание учащихся привлекается к числам, данным в задаче. Решение описывается словами: «пять и три – это восемь», «пять без двух – это три», «три по два – это шесть», «восемь на два – это четыре». Ответ задачи пока находится также пересчитыванием.
На третьем этапе после введения знаков +, -, *, :, = учащиеся переходят к обычным записям решения задач.
Слайд 9По реке катер проплыл _______
км, а по морю в ______ раз
Придумай числовые данные, подставь их в условие задачи и реши ее.
Слайд 10Решение:
12:3=4 (с.)
Ответ: 4 слова.
Придумай вопрос к задаче, чтобы она решалась двумя
Вопрос:
Петя списал с доски 12 слов. Треть этих слов он записал в тетради неверно. Сколько слов Петя написал с ошибками?
Сколько слов Петя написал без ошибок?
Реши получившуюся задачу.
Слайд 11В конюшне 18 лошадей. Сколько упряжек получится, если лошадей запрячь парами?
Ответ:
Сколько упряжек получится, если лошадей запрячь тройками?
Ответ: ___________ .
Решение задач без выполнения записей.
Слайд 12Решение:
1) * 4 =
2)
Ответ: ___________ .
Литр лимонада стоит 3 р. Ребята купили 4 двухлитровых бутылки лимонада. Сколько денег они заплатили?
Слайд 13Было - ?
Взяли – 81 кн. и 135 кн.
Осталось – 574
Рассмотри краткую запись задачи. Закончи решение.
Решение:
1) 135 2)
+ 81
Ответ: _____________ .
Слайд 14Придумай вопрос к условию задачи, чтобы ее можно было решить по
* - * = (кг)
Вопрос:
Сахар разложили в 3 мешка по 50 кг и в 4 мешка по 20 кг.
На сколько кг сахара больше в трех мешках?
Запиши решение.
Слайд 15Таким образом, в процессе решения задач ребенок учится моделировать, выбирать наиболее
Слайд 17Ведущую роль в осознании текста, отношений, поиска пути решения и выбора
Слайд 18Найдите задачу
1.«У Тани 4 гриба».
2.«У Тани 4 гриба, а у Саши
3.«У Тани 4 гриба, а у Саши - 2 гриба. Сколько грибов у Тани и Саши вместе?»
4.«На сколько яблок больше, чем груш?»
Слайд 25Задание 1.
Прочитай текст справа и текст слева.
Петя поймал утром двух крабов,
Сколько всего крабов поймал Петя?
ЗАДАЧА
Петя поймал утром двух крабов, а вечером ещё одного.
УСЛОВИЕ ЗАДАЧИ
?
Чем отличается текст задачи от текста условия?
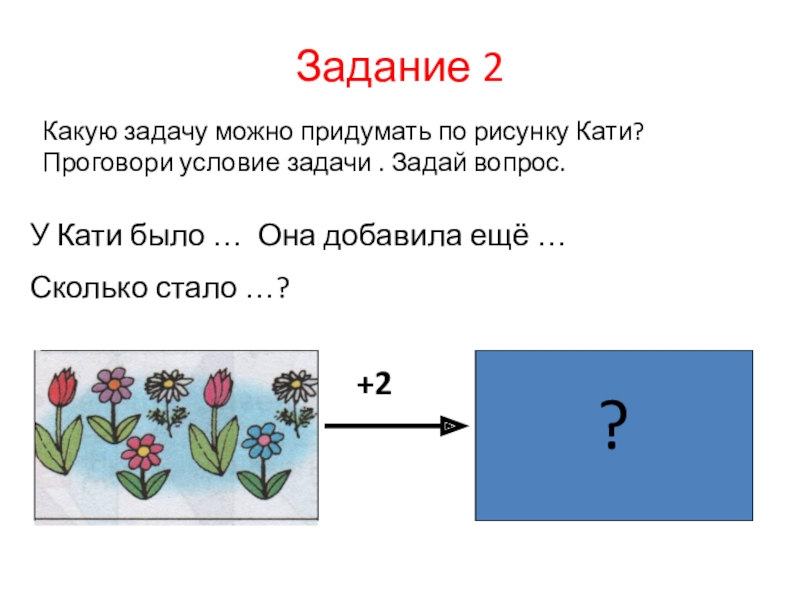
Слайд 26Задание 2
Какую задачу можно придумать по рисунку Кати? Проговори условие задачи
У Кати было … Она добавила ещё …
Сколько стало …?
+2
?
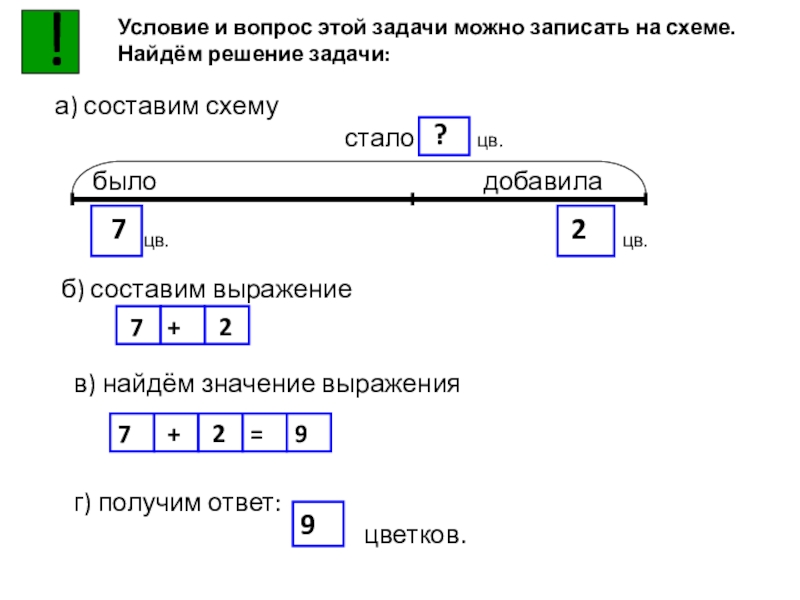
Слайд 27!
Условие и вопрос этой задачи можно записать на схеме. Найдём решение
а) составим схему
было
добавила
стало
?
цв.
7
цв.
2
цв.
б) составим выражение
7
+
2
в) найдём значение выражения
7
+
2
=
9
г) получим ответ:
9
цветков.
Слайд 28 Таким образом, к 3-му, 4-му классам учащимся предлагается
Слайд 30 Развивающая система Л.В. Занкова стремится сформировать у
Слайд 31Структура работы с задачами, которая предлагается в
занковской системе
Слайд 32Наибольшее внимание в учебниках математики по системе Л.В. Занкова (авторы И.И.
преобразование текстов, не являющихся задачами, в задачи;
изменение вопроса так, чтобы действий в решении стало больше (меньше);
изменение условия так, чтобы действий в решении стало больше (меньше);
изменение вопроса (условия, данных) так, чтобы задача стала нерешаемой;
внесение в задачу таких изменений, чтобы в ней появились лишние (недостающие) данные;
внесение в задачу таких изменений, чтобы в ней исчезли лишние (недостающие) данные;
изменение текста задачи так, чтобы в её решении появилось обратное действие.
Слайд 33В учебниках 1 класса присутствуют специальные задания, которые целенаправленно готовят детей
- восстановление развития сюжета по серии картинок (задания 7, 50: 1 кл., ч. 1);
- составление различных рассказов математического содержания к одному сюжетному рисунку (задания 97: ч.1., 45, 58, 90: ч.2., 105, 132, 135: ч.3.);
- завершение серии рисунков до полного восстановления текста (задание 84: ч.1.).
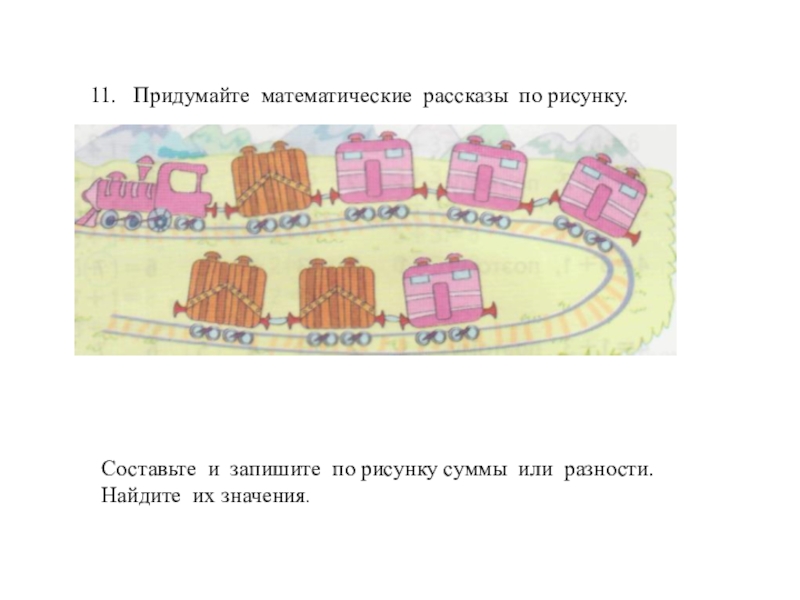
Слайд 3411. Придумайте математические рассказы по рисунку.
Составьте и запишите по рисунку
Найдите их значения.
Слайд 3523. Придумайте по рисунку два математических рассказа.
Запишите по каждому рассказу
К какому рассказу можно записать равенство 2 + 5 — 7?
К какому рассказу подойдёт равенство 5 + 2 = 7?
Слайд 36Рассмотри рисунки ниже. Чем они отличаются от верхних?
Какой математический рассказ
Чем отличаются математические рассказы, составленные по верхним и по нижним рисункам?
Лиза составила такой математический рассказ:
Было 5 снегирей. Прилетели ещё 3. Сколько снегирей стало?
В чём отличие рассказа Лизы от рассказа, составленного по верхним рисункам?
Лиза составила задачу.
Составь задачу по рисункам. Запиши её.
Слайд 3788. Выбери из трёх текстов задачу.
а) На ладонь упали снежинки. Потом ещё
несколько
б) На ладонь упало 4 снежинки. Потом ещё 2 снежинки. Была зима.
в) На ладонь упало 4 снежинки. Потом ещё 2 снежинки. Сколько всего снежинок упало на ладонь?
Реши задачу. Для этого запиши выражение и найди его значение.
Слайд 39
Задание 58 (ч.2). Придумай математический рассказ к рисунку.
Рисунок: по небу летят
По небу летели 6 чёрных птиц и 3 белых птицы. Всего летели 9 птиц.
Всего по небу летели 9 птиц. 4 птицы улетели вперёд, а 5 птиц отстали.
Летели по небу 4 птицы, их догнали ещё 5 птиц. Их стало 9.
Летели две стаи птиц. В одной стае было 3 чёрных и 1 белая птица. В другой стае столько же чёрных, а белых 2.
В небе было 9 птиц, но 4 птицы хотят улететь. Когда они улетят, останется 5 птиц.
Слайд 40 Во втором классе
начинается овладение одним их
главных аспектов математического образования
умением решать
задачи.
Слайд 41 Работа над задачами осуществляется в трёх основных направлениях:
-анализ текста с точки
-установление взаимосвязи между всеми найденными частями задачи;
-осознание роли каждой из частей в тексте задачи.
Результатом проведённых наблюдений становится: - осознание того, что данные всегда находятся в условии, а искомое – в вопросе; - осознание того, что отсутствие хотя бы одной из перечисленных частей задачи приводит к тому, что она перестаёт существовать как таковая; - осознание связи между изменением любой части задачи и её решением.
Слайд 42 Виды заданий
2 класс,ч.2 с.11
271 1) Дед Мороз и Снегурочка привезли в
Этот текст можно считать задачей?
2) Дополни текст до задачи. Реши ее.
3) Составь новую задачу, используя другие числа.
4) Сравни решения задач. В чем сходство? В чем их различие?
5) Если сможешь, дополни текст так, чтобы решение задачи стало другим. Реши задачу.
2 класс,ч.2 с.9
267 1) Реши задачу.
На столе стояло 7 стаканов с компотом. Выпили 5 стаканов компота. Сколько стаканов осталось на столе?
2) Сравни свое решение с таким:
Осталось 2 стакана. Осталось 7 стаканов.
Какое из них ты считаешь верным? Почему?
Проверь ответ: осталось 7 стаканов. Объясни, почему этот ответ верный.
3) Как нужно изменить вопрос задачи, чтобы верным был ответ: осталось 2 стакана.
Слайд 43Задание №112 (2 кл.). 1) Прочитай тексты и докажи, что это
Реши задачи и объясни выбор действий.
Придумай свою задачу, которую нужно решить тем же действием, что и первую из данных.
Измени вопрос своей задачи так, чтобы её решение стало таким же, как у второй данной задачи.
Слайд 44 Большое внимание в программе уделяется задачам с недостающими
В трёх коробках 58 ёлочных игрушек. В первой коробке 23 игрушки. Сколько игрушек в третьей коробке?
Дети дополняют задачу любыми данными о второй коробке, и получают возможность найти ответ на вопрос исходного текста.
Например: В трёх коробках 58 ёлочных игрушек. В первой коробке 23 игрушки, во второй – 18 игрушек. Сколько игрушек в третьей коробке?
Слайд 45 В учебниках различных УМК представлены задачи разного уровня сложности по
Слайд 46Список используемой литературы
Сборник программ к комплекту учебников «Начальная школа XXI века.»
Математика: 3 класс: методика обучения/ В.Н. Рудницкая, Т.В. Юдачева. – 2-е изд., перераб. – М.: Вентана – Граф, 2011. – 6-8с.
Математика: 3 класс: рабочая тетрадь № 1,2 для учащихся общеобразовательных учреждений/ В.Н. Рудницкая, Т.В. Юдачева. – 2-е изд., перераб. – М.: Вентана – Граф, 2011.














































![Презентация по обучению грамоте Звук [a], буква А](/img/thumbs/27ff9ec738c536e9548b36d4d64bc811-800x.jpg)

