- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер - класс Решение задач по технологии УДЕ
Содержание
- 1. Мастер - класс Решение задач по технологии УДЕ
- 2. Слайд 2
- 3. Слайд 3
- 4. Одним из технологических примеров УДЕ, повышающих
- 5. Слайд 5
- 6. Предлагается решить две задачи:
- 7. Заметьте: число 6 повторяется дважды.Проанализировав решения, возникают
- 8. 1.На основе этой формулы можно предложить задания:Составить
- 9. После знакомства с понятиями «увеличение» и «уменьшение»
- 10. При обучении решению текстовых задач необходимо достигнуть
- 11. Слайд 11
- 12. Слайд 12
- 13. ов.
- 14. Слайд 14
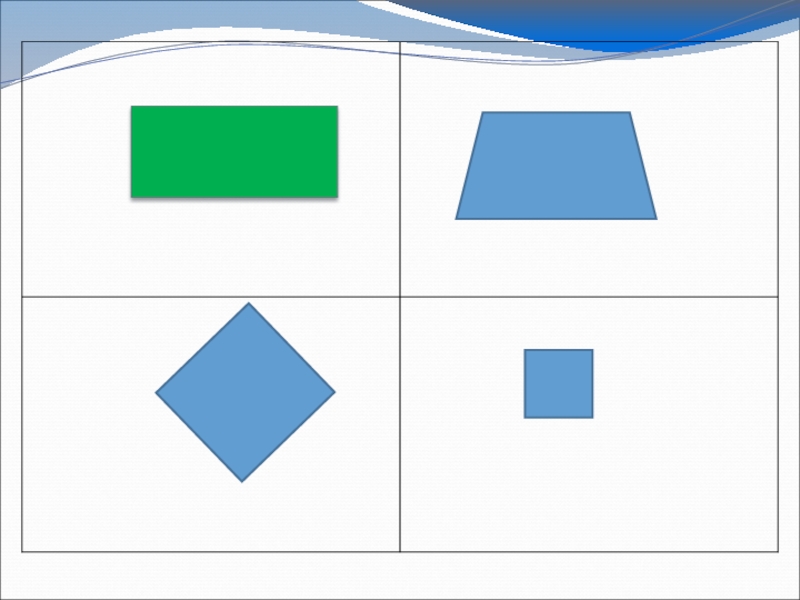
- 15. Особое внимание уделяю решению геометрических задач. Сначала
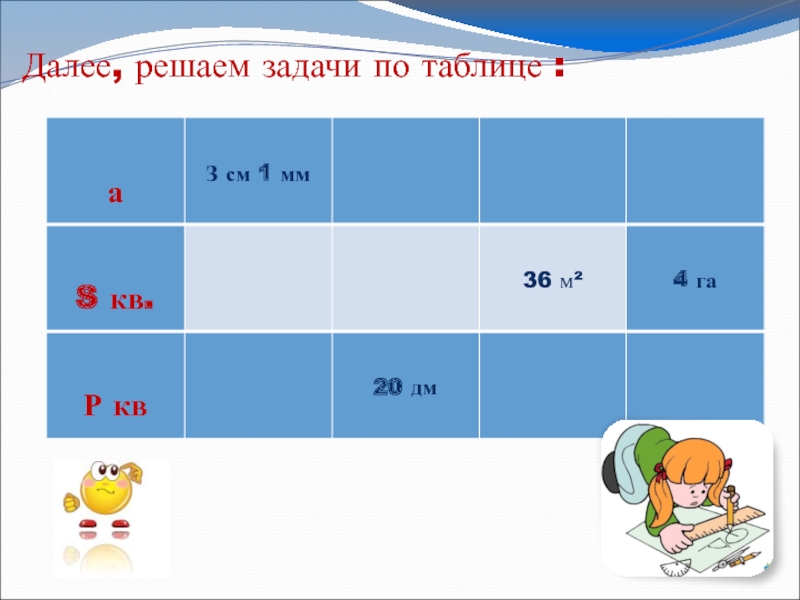
- 16. Далее, решаем задачи по таблице :
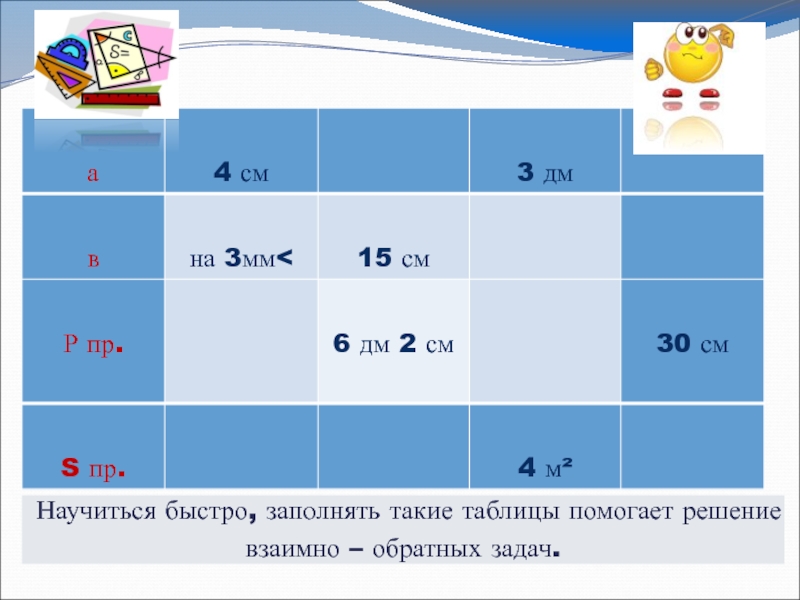
- 17. Научиться быстро, заполнять такие таблицы помогает решение взаимно – обратных задач.
- 18. За годы работы в школе я пришла
- 19. -- дает ученикам возможность умственной разминки (т.
- 20. Спасибо за внимание!
Слайд 1
учитель начальных классов
МБОУ «СОШ №4»
г. Элиста
Цебекова С.А.
Мастер- класс
Тема:
«Решение задач по технологии
Слайд 4
Одним из технологических примеров УДЕ, повышающих усвоение материала, является укрупнение
Если традиционная программа предлагает последовательное изучение материала, то при блочной подаче ученик имеет возможность сравнивать, анализировать, находить общее и различное.
Опыт работы показывает, что при такой подаче ребята легче воспринимают и усваивают материал.
Слайд 5
«Формирование и обобщение умений решать задачи на основе технологии УДЕ»
В процессе
Слайд 6
Предлагается решить две задачи:
Задача на уменьшение
В коробке лежало 6 цветных карандашей,
6 – 4 = 2 (к) –простых
6 + 2 = 8 (к)
Ответ: 8 карандашей всего.
6 – 4 + 6 =8 (к)
Задача на увеличение
В коробке лежало 6 цветных карандашей, а простых на 4 больше. Сколько всего карандашей в коробке?
6 + 4 =10(к) -простых
10 + 6 =16 (к)
Ответ: 16 карандашей всего
6 + 4 + 6 =16 (к)
Слайд 7
Заметьте: число 6 повторяется дважды.
Проанализировав решения, возникают два вопроса:
- Что общего
- Чем отличаются задачи?
Отсюда вывод:
Если в задачи на увеличение( сложение) на больше, то задача решается по формуле: а + в +с;
Если в задаче уменьшение ( вычитание) на меньше, то задача решается по формуле: а – в + а, отсюда следует:
а + в + а
Через несколько уроков дети легко смогут решать задачи, используя эту формулу.
Слайд 8
1.На основе этой формулы можно предложить задания:
Составить задачу по краткой записи
Яблок – 9 кг
Груш - ? кг, на 4 кг<
9 + 4 + 9
9 - 4 + 4
9 - 4 + 9
9 + 4
а) Преобразуйте задачу по выражению 9 – 4; 9 + 4 + 9
б) Может ли быть решением задачи 9 + 4 + 9?
2. Найди верное решение. Высота сарая а м, что в м ниже дома. Найди высоту сарая и дома?
а – в + а
а + в +а
Составь и реши задачу, если а = 3 м, в = 2 см.
?
Слайд 9
После знакомства с понятиями «увеличение» и «уменьшение» в несколько раз и
Поэтому формула расширяется:
±
а × в + а
:
Учащиеся делают вывод:
а) если в задаче число увеличиваем на несколько единиц и находим сколько всего, то а + в + а;
б) если в задаче число уменьшаем на несколько единиц и находим сколько всего, то а - в + а;
в) если в задаче число увеличиваем в несколько раз и находим сколько всего, то а * в + а;
г) если в задаче число уменьшаем в несколько раз и находим сколько всего, то а : в + а.
Так ученики без особого труда со временем приучаются записывать решение задачи по формуле и практически не делают ошибок в решении задачи, учатся различать простую задачу от составной, а также готовятся к усвоению алгебраических выражений.
Слайд 10
При обучении решению текстовых задач необходимо достигнуть двух взаимосвязанных целей:
ОБУЧИТЬ
2. приемам поиска решения любой задачи
Достичь этих целей, помогает решение взаимообратных задач по системе УДЕ.
В учебнике П.М.Эрдниева для достижения первой цели задачи обобщаются в определенные виды. Например, задачи на приведение к единице: предлагается решить задачу прямую, а далее составляются и решаются три обратные.
Слайд 11
Задача:
С 8
8 ов. – 40 кг
5 ов. - кг.
1)40 : 8 = 5 (кг) – 1 ов.
2)5 * 5 =25 (кг) с 5 ов.
Ответ: 25 кг шерсти настригли с 5 овец.
Слайд 13
ов. -40 кг
1)25 :5 = 5 (кг) 1 ов.
2)40 : 5 = 8 (ов)
Ответ: 8 овец.
По аналогии прямой задаче составляются и обратные, далее выявляется полное и частичное сходство. Полное сходство в том, что в 1 действии находили, сколько состригли с 1 овцы, различие во втором действии.
Далее отрабатываются решения любых аналогичных задач.
Слайд 15Особое внимание уделяю решению геометрических задач. Сначала отрабатываем решение задач по
S кв = а * а Р пр = (а + в) * 2 S пр = а * в
Р кв = а * 4 а = Р : 2 – а а = S : в
а = Р : 4 в = Р : 2 – в в = S : а
Слайд 18
За годы работы в школе я пришла к выводу о необходимости
-показывает учащимся возможность использование аналогий для творческого поиска, отыскания новых ассоциаций и связей. Психологические исследования творческих процессов показывают, что возможности творческого поиска расширяется благодаря сопоставлениям, сравнениям. Образное мышление на основе метафорических сравнений многие считают «природной способностью» детей, однако и эта способность нуждается в поддержке и развитии (н/р: решение прямых и обратных задач);
Слайд 19
-- дает ученикам возможность умственной разминки (т. е. использовать «разогревающие» упражнения);
-
- поддерживать живость воображения (необходимо поддерживать проявления свободного воображения в учебной обстановке, т.к они служат основой творческого мышления);
- расширение фонда знаний (усвоение информации не заменяет и само по себе не развивает умение думать, но технология УДЕ «заставляет» ребенка думать.