- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Черчение и перспектива на тему Деление окружности на равные части и построение правильных многоугольников (1 курс)
Содержание
- 1. Презентация по дисциплине Черчение и перспектива на тему Деление окружности на равные части и построение правильных многоугольников (1 курс)
- 2. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ Для
- 3. Деление на три равные части
- 4. Деление на три равные части1. Чертим центровые линии будущей окружности.
- 5. Деление на три равные части2. Из центра О проводим дугу окружности заданного радиуса (R).
- 6. Деление на три равные части3. Обозначаем точки
- 7. Деление на три равные части4. Из точки
- 8. Деление на три равные части5. Соединяем с
- 9. Деление на четыре равные части
- 10. Деление на четыре равные части1. Чертим центровые линии будущей окружности.
- 11. Деление на четыре равные части2. Из центра О проводим дугу окружности заданного радиуса (R).
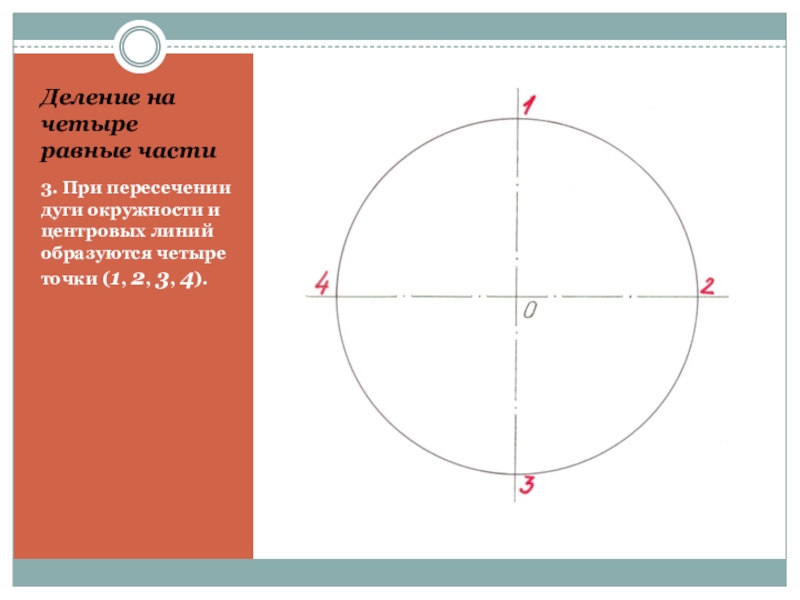
- 12. Деление на четыре равные части3. При пересечении
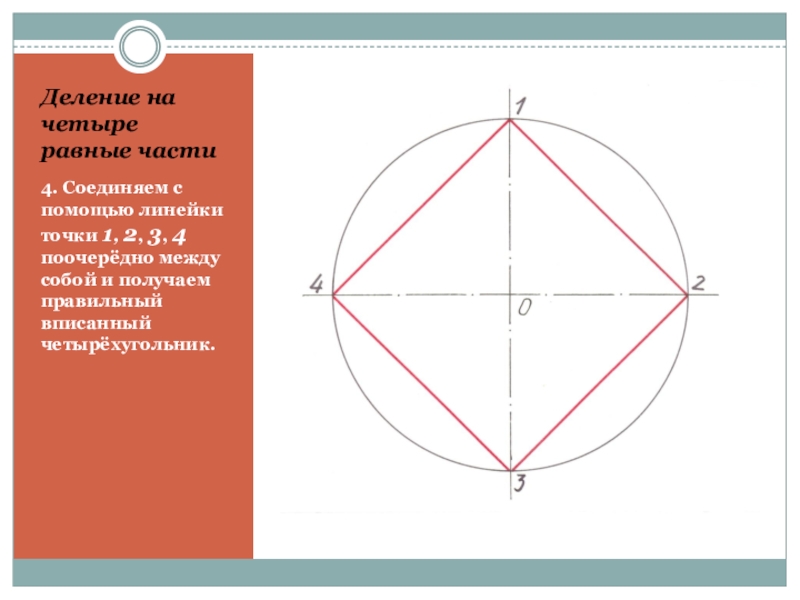
- 13. Деление на четыре равные части4. Соединяем с
- 14. Деление на пять равных частей
- 15. Деление на пять равных частей1. Чертим центровые линии будущей окружности.
- 16. Деление на пять равных частей2. Из центра О проводим дугу окружности заданного радиуса (R).
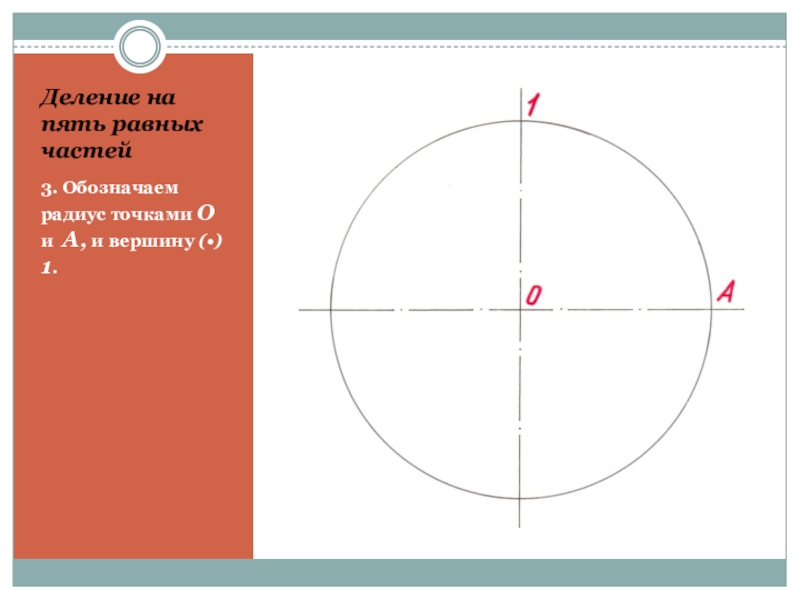
- 17. Деление на пять равных частей3. Обозначаем радиус точками О и А, и вершину (•) 1.
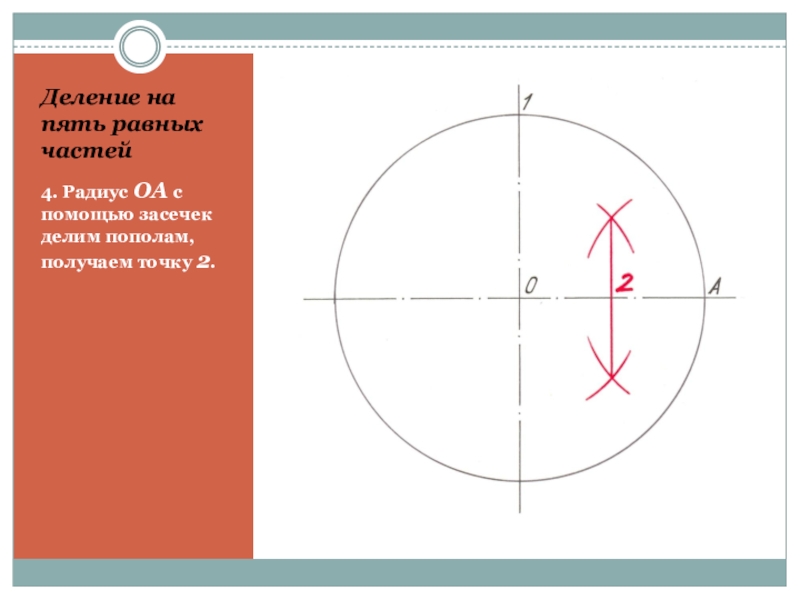
- 18. Деление на пять равных частей4. Радиус ОА с помощью засечек делим пополам, получаем точку 2.
- 19. Деление на пять равных частей5. Точку 2 соединяем с вершиной (•) 1.
- 20. Деление на пять равных частей6. Из точки
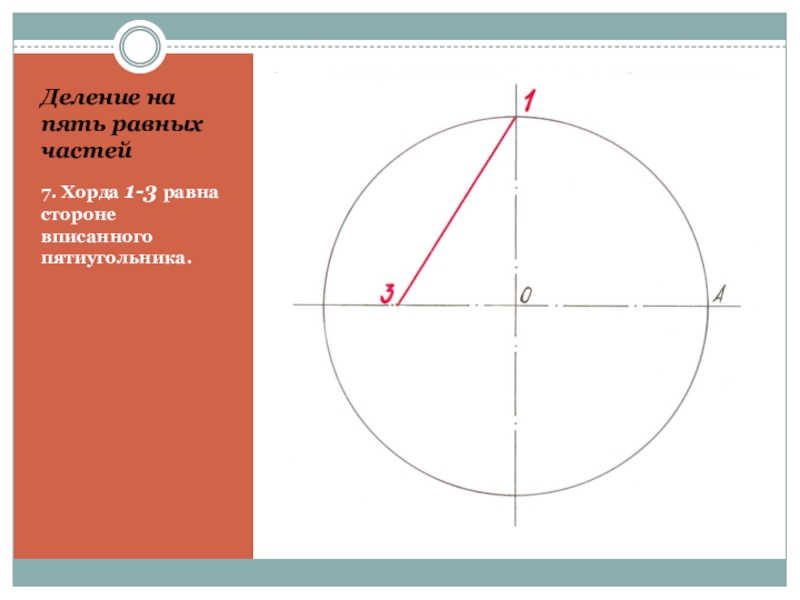
- 21. Деление на пять равных частей7. Хорда 1-3 равна стороне вписанного пятиугольника.
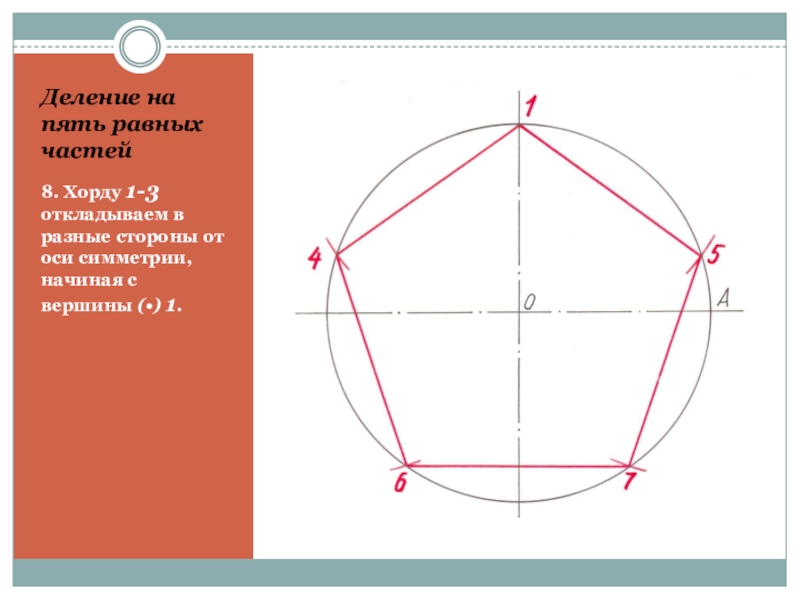
- 22. Деление на пять равных частей8. Хорду 1-3
- 23. Деление на шесть равных частей
- 24. Деление на шесть равных частей1. Чертим центровые линии будущей окружности.
- 25. Деление на шесть равных частей2. Из центра О проводим дугу окружности заданного радиуса (R).
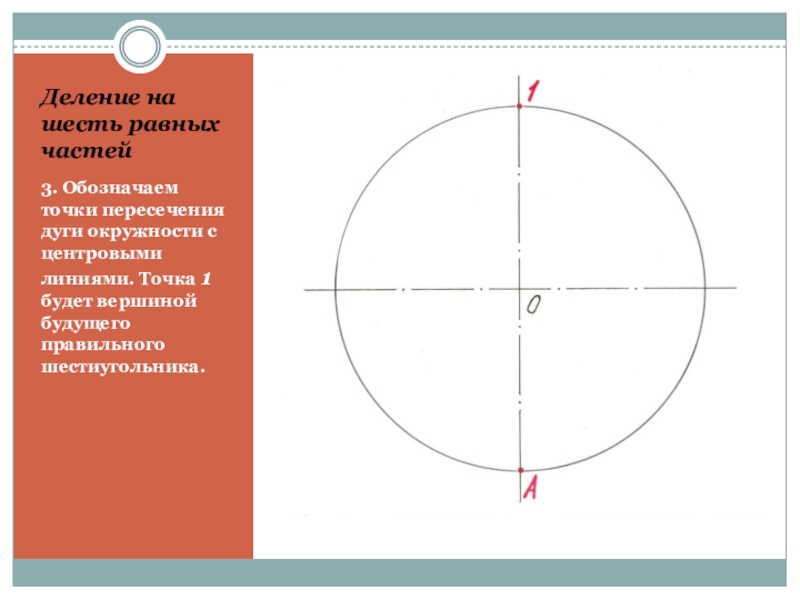
- 26. Деление на шесть равных частей3. Обозначаем точки
- 27. Деление на шесть равных частей4. Из точек
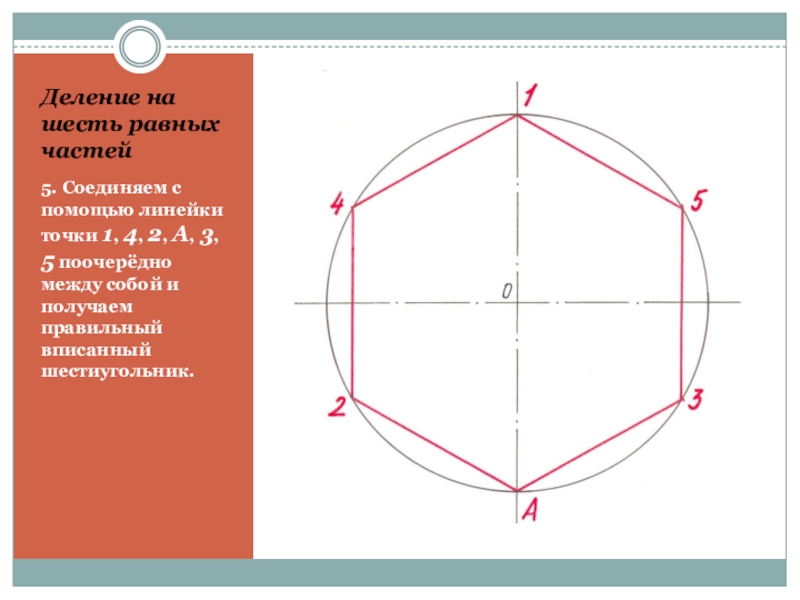
- 28. Деление на шесть равных частей5. Соединяем с
- 29. Спасибо за внимание!
ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ Для построения чертежей некоторых деталей необходимо уметь делить окружность на равные части и строить правильные многоугольники.
Слайд 1Выполнил: Е.Н. Дубровская, преподаватель художественных дисциплин
ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
Слайд 2ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
Для построения чертежей некоторых деталей
необходимо уметь делить окружность на равные части и строить правильные многоугольники.
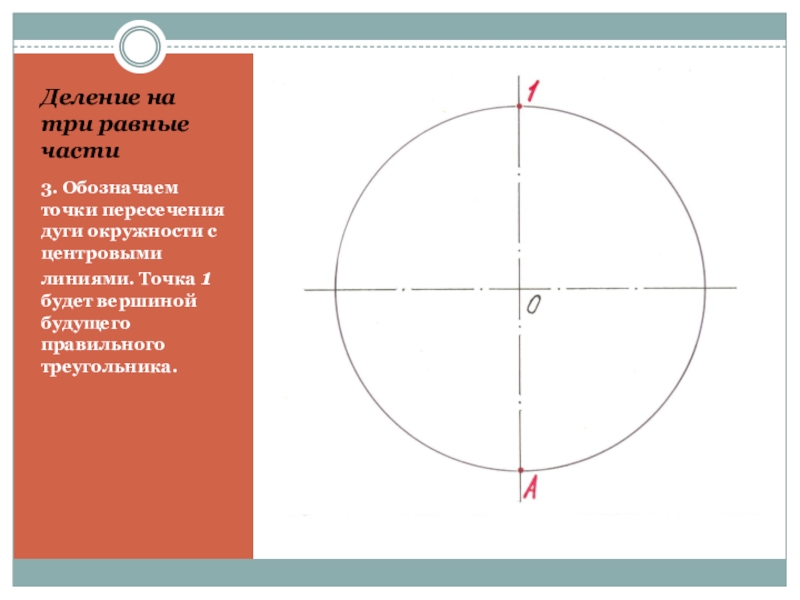
Слайд 6Деление на три равные части
3. Обозначаем точки пересечения дуги окружности с
центровыми линиями. Точка 1 будет вершиной будущего правильного треугольника.
Слайд 7Деление на три равные части
4. Из точки А тем же заданным
радиусом проводим дугу окружности. При пересечении дуг окружностей получаем две точки 2 и 3.
Слайд 8Деление на три равные части
5. Соединяем с помощью линейки точки 2,
1, 3 поочерёдно между собой и получаем правильный вписанный треугольник.
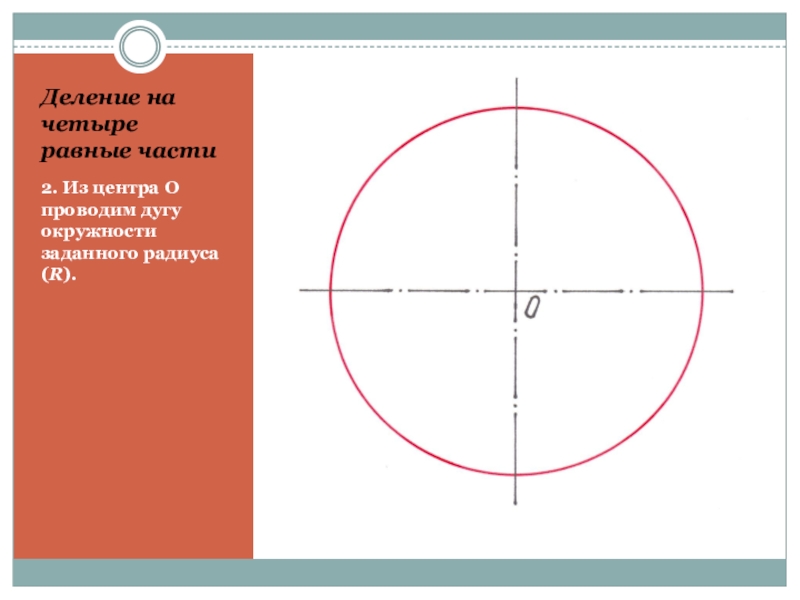
Слайд 11Деление на четыре равные части
2. Из центра О проводим дугу окружности
заданного радиуса (R).
Слайд 12Деление на четыре равные части
3. При пересечении дуги окружности и центровых
линий образуются четыре точки (1, 2, 3, 4).
Слайд 13Деление на четыре равные части
4. Соединяем с помощью линейки точки 1,
2, 3, 4 поочерёдно между собой и получаем правильный вписанный четырёхугольник.
Слайд 18Деление на пять равных частей
4. Радиус ОА с помощью засечек делим
пополам, получаем точку 2.
Слайд 20Деление на пять равных частей
6. Из точки 2 через вершину (•)
1 проводим дугу до пересечения в точке 3 с центровой линией.
Слайд 22Деление на пять равных частей
8. Хорду 1-3 откладываем в разные стороны
от оси симметрии, начиная с вершины (•) 1.
Слайд 25Деление на шесть равных частей
2. Из центра О проводим дугу окружности
заданного радиуса (R).
Слайд 26Деление на шесть равных частей
3. Обозначаем точки пересечения дуги окружности с
центровыми линиями. Точка 1 будет вершиной будущего правильного шестиугольника.
Слайд 27Деление на шесть равных частей
4. Из точек А и 1 тем
же заданным радиусом проводим дуги окружностей. При пересечении дуг окружностей получаем четыре точки 2 и 3; 4 и 5.
Слайд 28Деление на шесть равных частей
5. Соединяем с помощью линейки точки 1,
4, 2, А, 3, 5 поочерёдно между собой и получаем правильный вписанный шестиугольник.