- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи к курсу Основы теории вероятностей
Содержание
- 1. Задачи к курсу Основы теории вероятностей
- 2. На слайдах представлены задачи и их решение,
- 3. Доска Гальтона
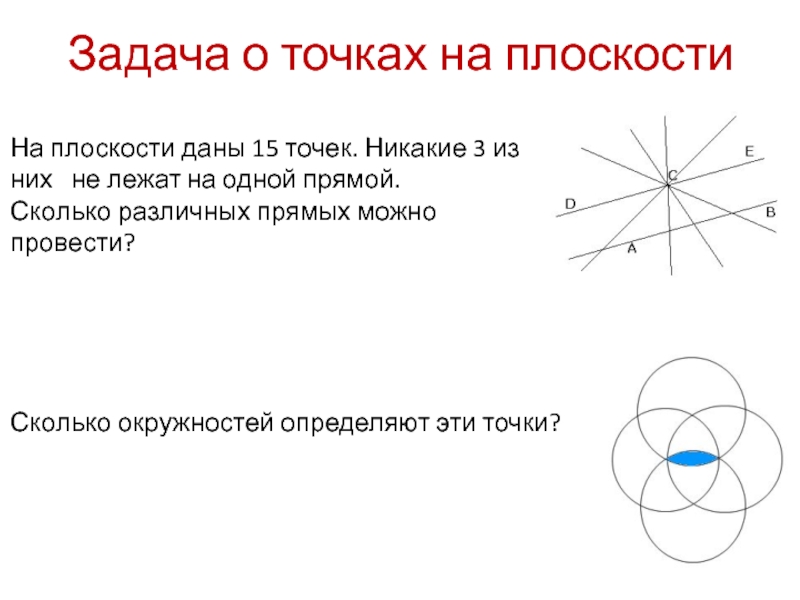
- 4. Задача о точках на плоскостиНа плоскости даны
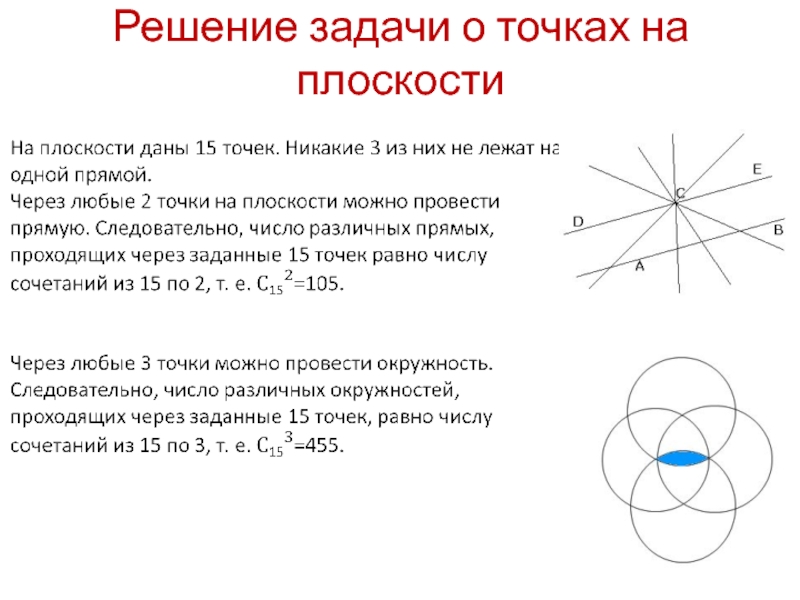
- 5. Решение задачи о точках на плоскости
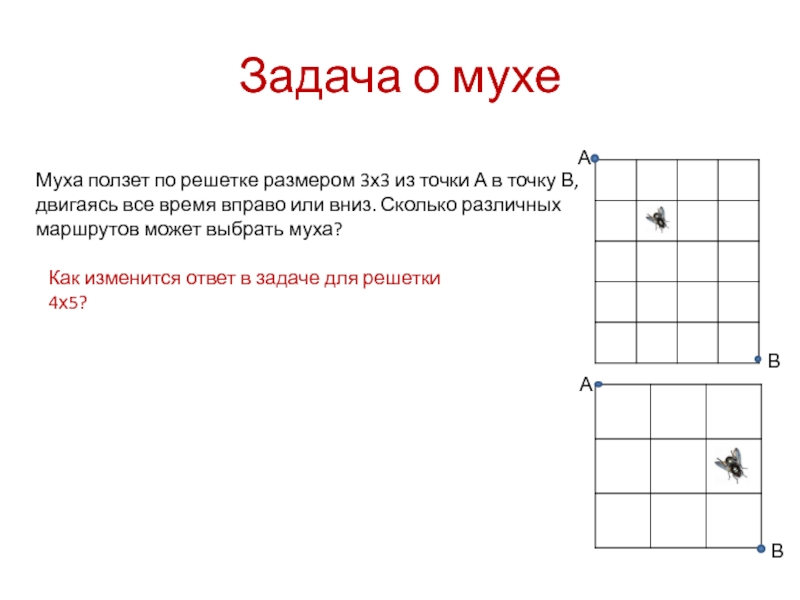
- 6. Задача о мухеАВАВМуха ползет по решетке размером
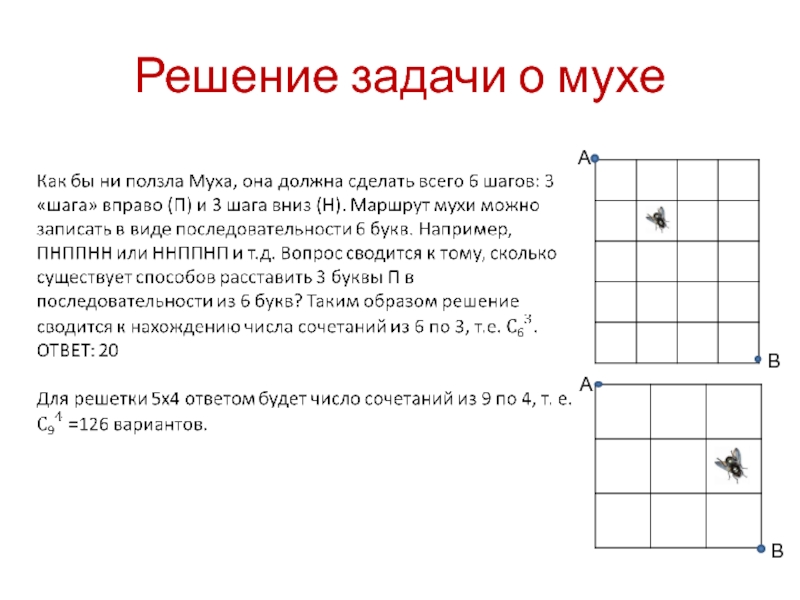
- 7. Решение задачи о мухеАВАВ
- 8. Встреча в кафе…12 друзей решили встречаться каждый
- 9. Решение задачи о встрече в кафе
- 10. Турнир по шахматамНа шахматном турнире было сыграно
- 11. Решение задачи о шахматном турниреПусть первоначально было
- 12. Задача о ладьяхБелую ладью можно поставить
- 13. Задача о встречеДва студента договорились встретиться в
- 14. Решение задачи о встрече
- 15. Задача о звездочетеНекий властелин разгневался на звездочета
- 16. Решение задачи о звездочетеПусть звездочет положит в
- 17. Задача «Блуждание в лабиринте»На рисунке изображен
- 18. Решение задачи «Блуждание в лабиринте»Пройдя от
- 19. Задача об отличном билете Назовем билет с номером
- 20. Задача «О кассире»Чтобы быстрее подсчитать мелочь в
- 21. Решение задачи «О кассире»
- 22. Задача «Игра в шахматы»Остап Бендер играет 8
- 23. Решение задачи «Игра в шахматы»
- 24. В урну, содержащую два шара , опущен
- 25. Решение задачи о шарах в урнеОбытие А-извлечен
- 26. РешениеСобытие А – в каждом из двух
- 27. РешениеВведем гипотезы о цвете извлеченных шаров из
Слайд 1Задачи к курсу «Основы теории вероятностей»
Учитель математики
высшей квалификационной
категории Кучеренко Н.
Слайд 2На слайдах представлены задачи и их решение, которые вызывают большой интерес
Слайд 4Задача о точках на плоскости
На плоскости даны 15 точек. Никакие 3
Сколько различных прямых можно провести?
Сколько окружностей определяют эти точки?
Слайд 6Задача о мухе
А
В
А
В
Муха ползет по решетке размером 3х3 из точки А
Как изменится ответ в задаче для решетки 4х5?
Слайд 8Встреча в кафе…
12 друзей решили встречаться каждый год в
одном кафе.
обмениваться впечатлениями за столиком по 4
человека. Сколько лет им понадобится, чтобы
каждый мог посидеть с каждым из остальных за
каким – либо одним столиком?
Слайд 10Турнир по шахматам
На шахматном турнире было сыграно 130
партий, все участники
по одной партии, но два участника выбыли
из соревнований после того,
как сыграли по 5 партий каждый.
Сколько было первоначально участников турнира?
Слайд 11Решение задачи о шахматном турнире
Пусть первоначально было
Х+2 игрока, а осталось
ков. Они сыграли 130-10=120 партий.
Получим уравнение
Х (Х-1)/2=120
Значит, Х=16.
Первоначально было 18 играков.
Слайд 12 Задача о ладьях
Белую ладью можно поставить на любую из 64
Она побьёт 15 клеток: 7 по вертикали, 7 по горизонтали и ту,
на которой она стоит, независимо, где бы она
не стояла. Остается 64 - 15=49 мест, чтобы поставить
черную ладью. Значит, число способов поставить обе ладьи
так, чтобы они не били друг друга равно 64*49=3136.
Ответ: 3136 способов.
Сколькими способами можно поставить на шахматном поле белую и черную ладьи так, чтобы они не били друг друга.
Решение
Слайд 13Задача о встрече
Два студента договорились встретиться в некотором месте между 9
Причем, каждый ждет другого в течение 15 минут, а затем уходит. Какова вероятность, что они встретятся?
Слайд 15Задача о
звездочете
Некий властелин разгневался на звездочета и повелел палачу отрубить ему
Слайд 16Решение задачи о звездочете
Пусть звездочет положит в каждую урну по 1
Вероятность спастись будет также равна ½, если звездочет положит
в одну урну 2 белых шара, а в другую 2 черных (рис. б). Палач
с равной вероятностью может подойти как к «белой», так и к
«черной» урне.
Пусть звездочет положит в одну урну белый шар, а в другую 1 белый и 2 черных (рис. в). Если палач подойдет к 1-ой урне, то звездочет спасется наверняка (Р=1). Если палач подойдет ко 2-ой урне, то вероятность спастись у звездочета Р=⅓. Так как Р выбора урны равна ½ , то полная вероятность спастись равна Р=(½*1)+(½*⅓)=⅔.
Если звездочет положит в одну урну черный шар, а в другую-
1черный и 2 белых (рис. г), то вероятность спастись –наименьшая:
Р=(½*0)+(½*⅔)= ⅓.
Таким образом, наибольшие шансы спастись соответствуют (рис. в).
Слайд 17Задача
«Блуждание в лабиринте»
На рисунке изображен лабиринт, в котором хранятся сокровища
Слайд 18Решение задачи
«Блуждание в лабиринте»
Пройдя от А до пункта 1, искатель
Вероятность выбора Р=⅓.Тогда вероятность попасть из А в пункт 3
равна Р= ½ * ⅓, т.е. повернуть в пункте 1 налево с Р= ½ и в пункте 2
налево с Р=⅓. Чтобы из А добраться из пункта 4, необходимо из пункта 3 с Р= ½ пройти прямо, т.е. Р= ½ * ⅓* ½. Ясно, что Р добраться из А в пункт 5 равна Р= ½ * ⅓* ½* ⅓.
Вероятность попасть из А в хранилище Р= ½ * ⅓* ½* ⅓* ½=1/72.
Вероятность попасть в западню и погибнуть равна Р=71/72.
Слайд 19Задача об отличном билете
Назовем билет с номером от 000000 до 999999
Решение
Слайд 20Задача «О кассире»
Чтобы быстрее подсчитать мелочь в конце рабочего дня, кассир
Слайд 22Задача «Игра в шахматы»
Остап Бендер играет 8 шахматных партий против членов
Слайд 24В урну, содержащую два шара , опущен белый шар, после чего
цвете шаров.
Задача о шарах в урне
Слайд 25Решение задачи о шарах в урне
Обытие А-извлечен белый шар. Возможны гипотезы
Вероятность извлечь белый шар вычисляем по формуле полной вероятности: Р(А)=1/3*1/3+1/3*2/3+1/3*1=2/3.
Слайд 26Решение
Событие А – в каждом из двух испытаний вынут белый шар.
В1
Условные вероятности: Р(А/В1)=10/16*9/15=15/40-вероятность вынуть белый шар
из первой урны в первом и втором испытании.
Р(А/В2)=7/16*6/15=7/40- вероятность подряд вынуть белый шар из второй урны.
Р(А)=1/2*15/40+1/2*7/40=1/2*22/40=11/40.
Третья задача о шарах
В одной из урн 10 белых и 6 черных шаров , в другой – 7 белых и 9 черных шаров. Произвольно выбирают урну и из нее вынимают шар. Он белый. Чему равна вероятность того, что и второй шарик, наугад вынутый из этой урны, окажется белым?
Слайд 27Решение
Введем гипотезы о цвете извлеченных шаров из каждой урны:
В1 -
В2 – из каждой урны извлечен черный шар. Р(В2)=2/10*16/20=4/25.
В3 – из урн извлечен 1белый и 1 черный шар. Р(В3)=8/10*16/20 + 2/10*4/20 = 17/25
Событие А – шар белый.
Рассмотрим условные вероятности: из двух шаров вынуть белый при этих гипотезах
Р(А/В1)=1, Р(А/В2)=0, Р(А/В3)=1/2, тогда по формуле полной вероятности
Р(А)=1*4/25+ 0*4/25 + 1/2*17/25=4/25+17/50 = ½.
Вторая задача о шарах в урне
В первой урне 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар. (Р=0,5)