- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи для повторения теории вероятностей при подготовке к экзаменам
Содержание
- 1. Задачи для повторения теории вероятностей при подготовке к экзаменам
- 2. Задачи на вероятность с игральным кубиком (игральная кость)
- 3. 1. Определите вероятность того, что при бросании
- 4. 2. Определите вероятность того, что при бросании
- 5. 3. Определите вероятность того, что при бросании
- 6. 4. Определите вероятность того, что при бросании
- 7. 5. Игральную кость бросают дважды. Найдите вероятность
- 8. 6. Игральную кость бросают дважды. Найдите вероятность
- 9. 7. Игральную кость бросают дважды. Найдите вероятность
- 10. Задачи на вероятность с монетами
- 11. 8. В случайном эксперименте симметричную монету бросают
- 12. 9. В случайном эксперименте симметричную монету
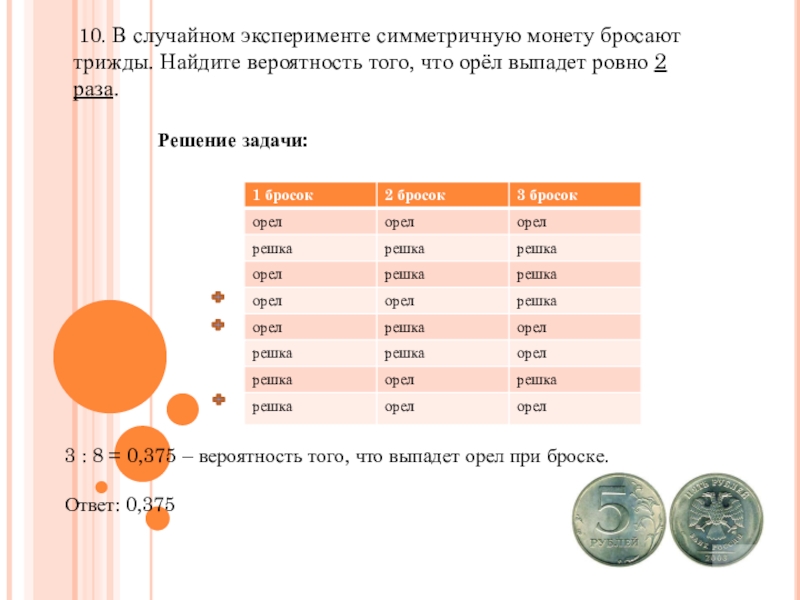
- 13. 10. В случайном эксперименте симметричную монету
- 14. 11. В случайном эксперименте симметричную монету бросают
- 15. Задачи на вероятность (разные)
- 16. 12. Известно, что в некотором регионе вероятность
- 17. 13. Известно, что в некотором регионе вероятность
- 18. 14. Стас выбирает трехзначное число. Найдите вероятность
- 19. 15. Андрей выбирает случайное трехзначное число. Найдите
- 20. 16. В каждой четвёртой банке кофе согласно
- 21. 17. На экзамене по геометрии школьнику достаётся
- 22. 18. Биатлонист пять раз стреляет по мишеням.
- 23. 19. В магазине стоят два платёжных автомата.
- 24. 20. В торговом центре два одинаковых автомата
- 25. 21. Две фабрики выпускают одинаковые стекла для
Слайд 31. Определите вероятность того, что при бросании игрального кубика (правильной кости)
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Нечетное число – 3 (1; 3; 5)
P = 3:6 = 0,5
Ответ: P=0,5
Слайд 42. Определите вероятность того, что при бросании игрального кубика (правильной кости)
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Менее 4–х очков – 3 (1; 2; 3)
P = 3:6 = 0,5
Ответ: P=0,5
Слайд 53. Определите вероятность того, что при бросании игрального кубика (правильной кости)
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Более 3–х очков – 3 (4; 5; 6)
P = 3:6 = 0,5
Ответ: P=0,5
Слайд 64. Определите вероятность того, что при бросании игрального кубика (правильной кости)
Решение задачи:
Всего событий – 6 (может выпасть 6 чисел от 1 до 6)
Более 2–х очков – 2 (3; 4; 5; 6)
P = 4:6 = 0,66…
Ответ: P=0,7
Слайд 75. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух
Решение задачи:
Сумма будет нечетна, когда:
1) в первый раз выпадет нечетное число, а во второй четное.
2) в первый раз - четное, а во второй раз нечетное.
1) 3 : 6 = 0,5 - Вероятность выпадения нечетного числа в первое бросание.
3 : 6 = 0,5 - Вероятность выпадения четного числа во второе бросание.
0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно.
2) 3 : 6 = 0,5 - Вероятность выпадения четного числа в первое бросание.
3 : 6 = 0,5 - Вероятность выпадения нечетного числа во второе бросание.
0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно,.
3) 0,25 + 0,25 = 0,5
Ответ: P=0,5
Слайд 86. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из
Решение задачи:
1) При первом броске выпадет 1, или 2, или 3, или 4, или 5, а при втором броске выпадет 5
2) При первом броске выпадет 5, а при втором броске выпадет 1, или 2, или 3, или 4, или 5
5 : 6 = 5/6 – вероятность того, что выпадут 1; 2; 3; 4; 5
1 : 6 = 1/6 - вероятность выпадения 5
5/6 · 1/6 = 5/36 - вероятность, что произойдут оба события
1 : 6 = 1/6 - вероятность выпадения 5
5 : 6 = 5/6 - вероятность выпадения 1; 2; 3; 4; 5
1/6 · 5/6 = 5/36 - вероятность, что произойдут оба события
5/36 + 5/36 = 10/36 = 5/18 = 0,277…
Ответ: 0,3
Слайд 97. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы
Решение задачи:
1) При первом броске выпадет 1, или 2, или 3, а при втором броске выпадет 4; или 5 или 6
2) При первом броске выпадет 4; или 5 или 6, а при втором броске выпадет 1, или 2, или 3.
3) При первом броске выпадет 4; или 5 или 6, а при втором броске выпадет 4, или 5, или 6.
3 : 6 = 0,5 - вероятность выпадения 1; 2; 3
3 : 6 = 0,5 - вероятность выпадения 4; 5; 6
0,5 · 0,5 = 0,25 - вероятность, что произойдут оба события
2) 3 : 6 = 0,5 - вероятность выпадения 4; 5; 6
3 : 6 = 0,5 - вероятность выпадения 1; 2; 3
0,5 · 0,5 = 0,25 - вероятность, что произойдут оба события
3) 3 : 6 = 0,5 - вероятность выпадения 4; 5; 6
3 : 6 = 0,5 - вероятность выпадения 4; 5; 6
0,5 · 0,5 = 0,25 - вероятность, что произойдут оба события
4) 0,25+ 0,25 + 0,25 = 0,75
Ответ: 0,75
Слайд 118. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,
2 : 4 = 0,5 - вероятность того, что выпадет орел при броске.
2) Ответ: 0,5
Решение задачи: Найдём число возможных исходов, переберём все варианты бросков. Составим таблицу и покажем все варианты:
Слайд 12 9. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность
1 : 8 = 0,125 – вероятность того, что выпадет орел при броске.
Ответ: 0,125
Решение задачи:
Слайд 13 10. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность
3 : 8 = 0,375 – вероятность того, что выпадет орел при броске.
Ответ: 0,375
Решение задачи:
Слайд 1411. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того,
Решение задачи:
1 : 8 = 0,125 - вероятность того, что выпадет орел при броске.
Ответ: 0,125
Слайд 1612. Известно, что в некотором регионе вероятность того, что родившийся младенец
Решение задачи:
1 - 0,512 = 0,488 – вероятность рождения девочек в регионе
2) 477 : 1000 = 0,477 – вероятность рождения девочек в 2010 г
3) 0,488 - 0,477=0,011
Ответ: 0,011
Слайд 1713. Известно, что в некотором регионе вероятность того, что родившийся младенец
Решение задачи:
1 - 0,486 = 0,514 – вероятность рождения девочек в регионе
2) 522 : 1000 = 0,522 – вероятность рождения девочек в 2011 г
3) 0,522 - 0,514 = 0,008
Ответ: 0,008
Слайд 1814. Стас выбирает трехзначное число. Найдите вероятность того, что оно делится
Решение задачи:
999 - 99 = 900 – всего трехзначных чисел
2) 999 : 48 = 20,8125 - т.е. всего 20 чисел делятся на 48
Из них два числа двузначные - это 48 и 96, то 20 – 2 = 18
4) 18 : 900 = 0,02
Ответ: 0,02
Слайд 1915. Андрей выбирает случайное трехзначное число. Найдите вероятность того, что оно
Решение задачи:
999 - 99 = 900 – всего трехзначных чисел
2) 999 : 33 = 30,29… - т.е. всего 30 чисел делятся на 33
Из них три числа двузначные - это 33, 66, 99 то 30 – 3 = 27
4) 27 : 900 = 0,03
Ответ: 0,03
Слайд 2016. В каждой четвёртой банке кофе согласно условиям акции есть приз.
Решение задачи:
1) 1 : 4 = 0,25 - вероятность выпадения приза.
2) 1 – 0,25 = 0,75 – вероятность не выпадения приза
Ответ: 0,75
Слайд 2117. На экзамене по геометрии школьнику достаётся один вопрос из списка
Решение:
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий: 0,35 + 0,2 = 0,52
Ответ: 0,52
Слайд 2218. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень
Решение:
вероятность попадания - 0,8
вероятность промаха – 0,2
События промаха и попадания независимы, значит
Ответ: 0,2
Слайд 2319. В магазине стоят два платёжных автомата. Каждый из них может
Решение:
Найдем вероятность, что неисправны оба автомата.
Эти события независимы, т.е. 0,12² = 0,0144
Событие, состоящее в том, что исправен хотя бы один
автомат – противоположное, значит 1 – 0,0144 = 0,9856
Ответ: 0,9856
Слайд 2420. В торговом центре два одинаковых автомата продают кофе. Вероятность того,
Решение:
Рассмотрим события:
А – кофе закончится в первом автомате
В – кофе закончится во втором автомате
А·В – кофе закончится в обоих автоматах
А+В - кофе закончится хотя бы в одном автомате
Значит, вероятность противоположного события (кофе останется в обоих автоматах) равна
Ответ: 0,56
Слайд 2521. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
Решение:
Вероятность того, что стекло, купленное на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135
Вероятность того, что стекло, купленное на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055
Значит, полная вероятность того, что случайно купленное в магазине стекло окажется бракованным: 0,0135 + 0,0055 = 0,019
Ответ: 0,019