- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Связь хроматического числа и степенной последовательности графа
Содержание
- 1. Связь хроматического числа и степенной последовательности графа
- 2. О раскраске графовВозникновение теории графов 1736 г.
- 3. Цели работы1) выявить зависимость хроматического числа графа
- 4. Понятие раскраски графаРаскраской графа называется такое приписывание
- 5. Примеры минимальной раскраски некоторых графовМинимальная раскраска колеса
- 6. Степенная последовательность графа
- 7. Первая задача исследованияЗадача 1. Пусть правильная степенная
- 8. Решение первой задачи исследования
- 9. Решение задачи
- 10. Построение раскраски
- 11. Вторая задача исследованияЗадача 2. Пусть правильная степенная
- 12. Решение второй задачи исследования
- 13. Вычислительные экспериментыРаспределение значений хроматического числа в зависимости от числа вершин n и от повторяющейся степени k
- 14. Результаты вычислительных экспериментов
- 15. Метод доказательства и примеры1) Выделение вершин наибольших степеней.2) Число ребер, соединяющих эти вершины
- 16. Примеры
- 17. Гипотеза и развитие задачи
- 18. Заключение
- 19. ПубликацияЗакорчемный Н.Т. Нахождение хроматического числа некоторых графов
- 20. Заключение
- 21. Благодарюза внимание!
О раскраске графовВозникновение теории графов 1736 г. – Л. Эйлер Задача о Кёнигсбергских мостахГипотеза четырех красок 1878 г. – А. Кэли Формулировка гипотезы 1976 г. – К. Аппель и В. Хейкен Компьютерное доказательство гипотезыНахождение хроматического числа
Слайд 2О раскраске графов
Возникновение теории графов
1736 г. – Л. Эйлер
Задача о Кёнигсбергских
мостах
Гипотеза четырех красок 1878 г. – А. Кэли Формулировка гипотезы 1976 г. – К. Аппель и В. Хейкен Компьютерное доказательство гипотезы
Нахождение хроматического числа графа – нерешенная в настоящее время задача
Гипотеза четырех красок 1878 г. – А. Кэли Формулировка гипотезы 1976 г. – К. Аппель и В. Хейкен Компьютерное доказательство гипотезы
Нахождение хроматического числа графа – нерешенная в настоящее время задача
Слайд 3Цели работы
1) выявить зависимость хроматического числа графа от повторяющихся степеней в
степенной последовательности графа;
2) получить формулу для оценки или определения хроматического числа графа, у которого в степенной последовательности только одно повторяющееся, не более трех раз, значение.
2) получить формулу для оценки или определения хроматического числа графа, у которого в степенной последовательности только одно повторяющееся, не более трех раз, значение.
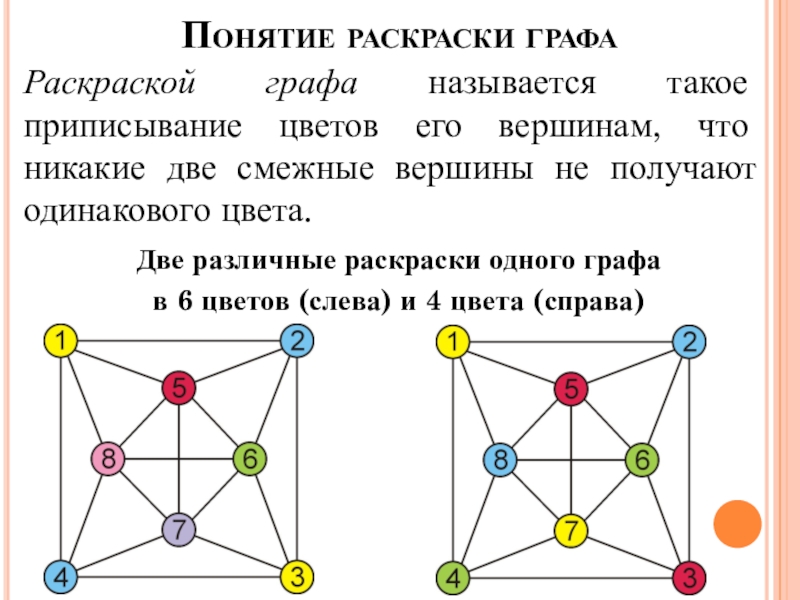
Слайд 4Понятие раскраски графа
Раскраской графа называется такое приписывание цветов его вершинам, что
никакие две смежные вершины не получают одинакового цвета.
Две различные раскраски одного графа
в 6 цветов (слева) и 4 цвета (справа)
Слайд 5Примеры минимальной раскраски некоторых графов
Минимальная раскраска
колеса с 4 вершинами в 4
цвета (слева) и колеса с 5 вершинами в 3 цвета (справа)
Слайд 7Первая задача исследования
Задача 1. Пусть правильная степенная последовательность графа с вершинами
n содержит ровно два одинаковых значения и значения 1 и
n – 1. В таком графе степени вершин – это числа 1, 2, …, n – 1 причем среди них ровно два повторяются. Задача исследования заключается в нахождении формулы хроматического числа таких графов.
Слайд 11Вторая задача исследования
Задача 2. Пусть правильная степенная последовательность графа с вершинами
n содержит ровно три одинаковых значения и значения 1 и
n – 1. В таком графе степени вершин – это числа 1, 2, …, n – 1 причем среди них ровно три повторяются, а одно отсутствует в последовательности. Задача исследования заключается в нахождении формулы хроматического числа таких графов.
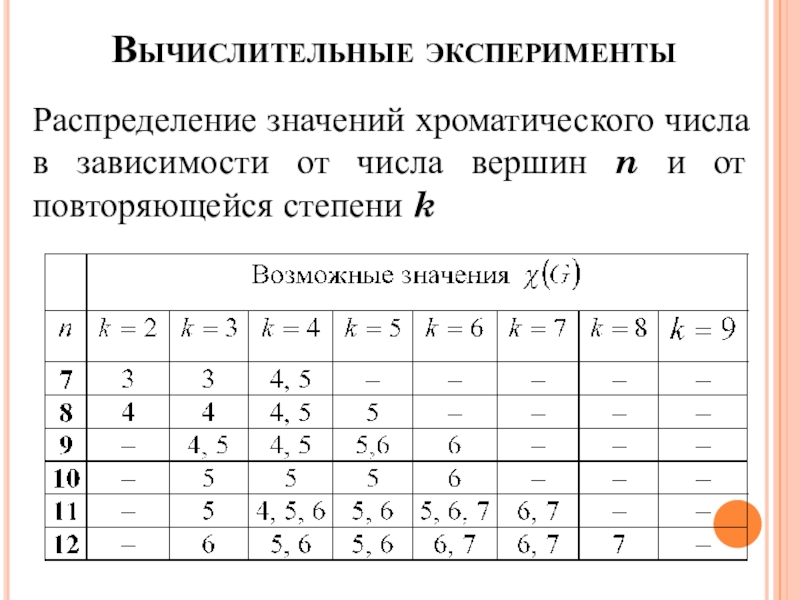
Слайд 13Вычислительные эксперименты
Распределение значений хроматического числа в зависимости от числа вершин n
и от повторяющейся степени k
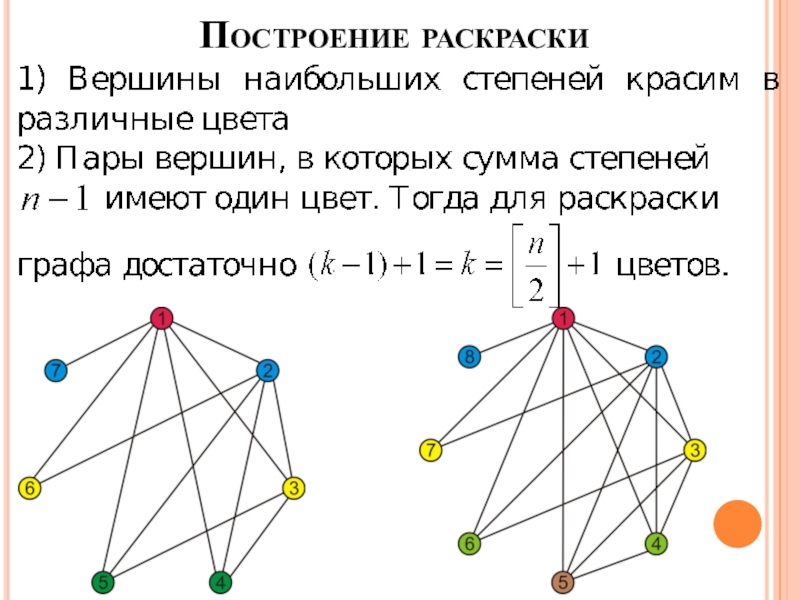
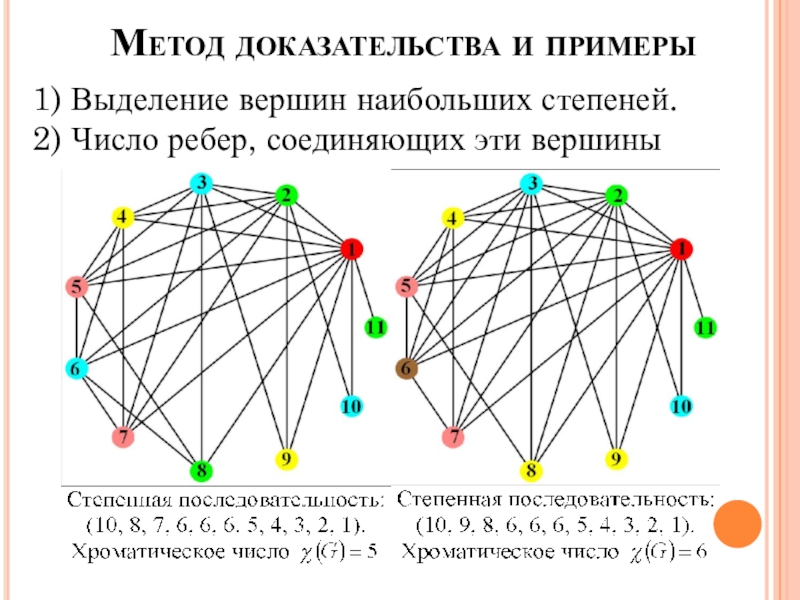
Слайд 15Метод доказательства и примеры
1) Выделение вершин наибольших степеней.
2) Число ребер, соединяющих
эти вершины
Слайд 19Публикация
Закорчемный Н.Т. Нахождение хроматического числа некоторых графов // Научные труды молодых исследователей
программы "Шаг в будущее". – 2013. – Т. 16. – С. 81 – 83.