- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Свойства функции
Содержание
- 1. Свойства функции
- 2. Понятие функцииЕсли каждому значению х из некоторого
- 3. Область определения и множество значений функцииОбластью определения
- 4. Свойства функций:монотонность Функцию y = f(x) называют
- 5. Свойства функций:ограниченность Функцию y = f(x) называют
- 6. Свойства функций:наибольшее и наименьшее значения функцииЧисло m
- 7. Свойства функций:четность или нечетность Функцию y =
- 8. Свойства функций:точки экстремумаТочку хо называют точкой максимума
- 9. Свойства функций:периодичность Говорят, что функция y =
- 10. График функцииГрафиком функции называется множество всех точек
- 11. Основные элементарныефункции, их свойстваи графики
- 12. Линейная функция y=kx+bСвойства линейной функции y =
- 13. xy0Линейная функция y=kx+bby = kx + b, k>0y = kx + b, k
- 14. Свойства функции y = k/x:D(f) = (–∞;
- 15. Обратная пропорциональность0xy
- 16. Свойства функции y = kx2 при k
- 17. Свойства функции y = kx2 при k
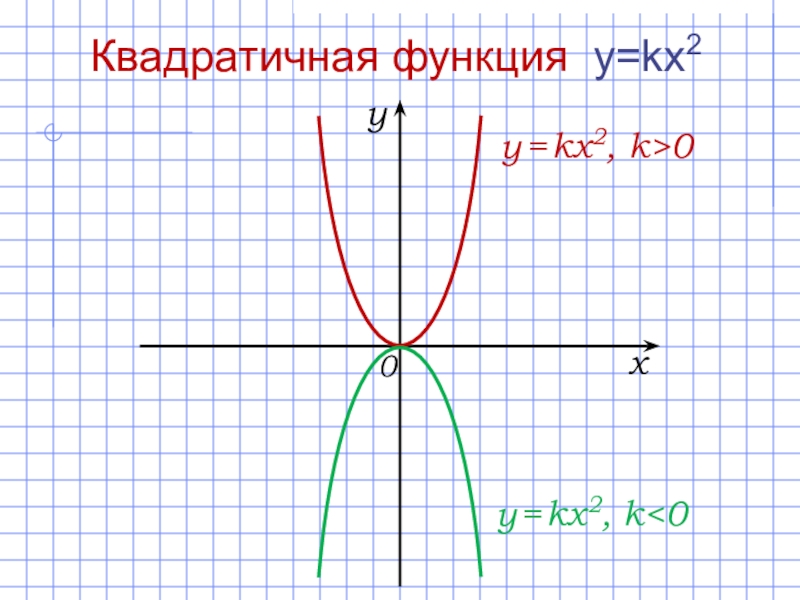
- 18. 0xyy = kx2, k>0Квадратичная функция y=kx2y = kx2, k
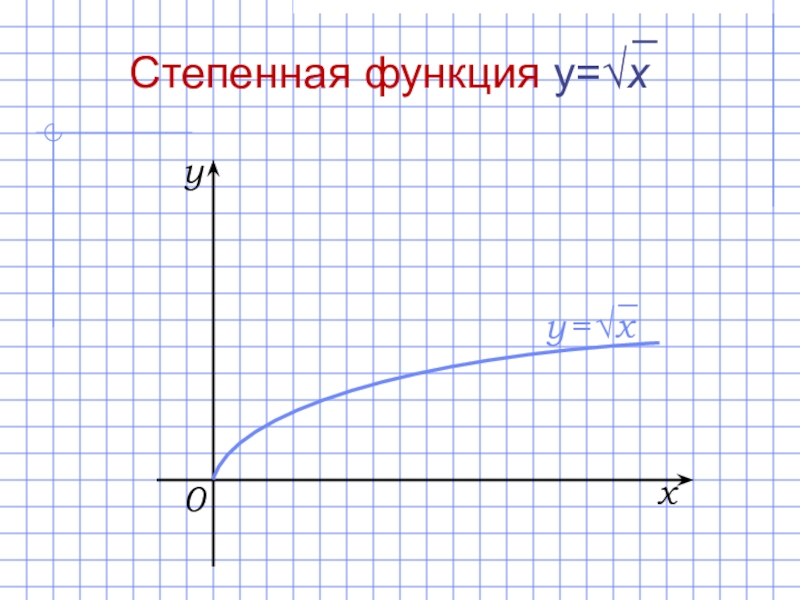
- 19. D(f) = [0; +∞).E(f) = [0; +∞).
- 20. 0xy
- 21. Свойства кубической функции y = x3:D(f) =
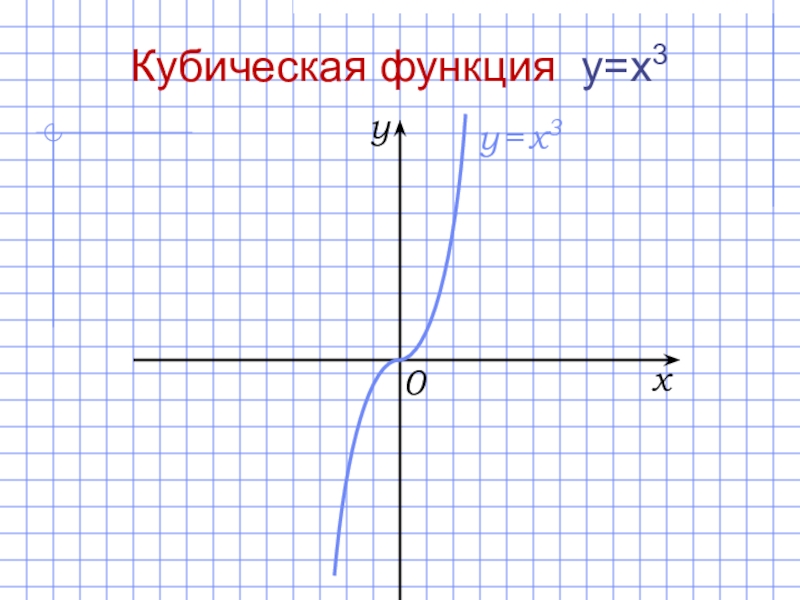
- 22. xy0y = x3Кубическая функция y=x3
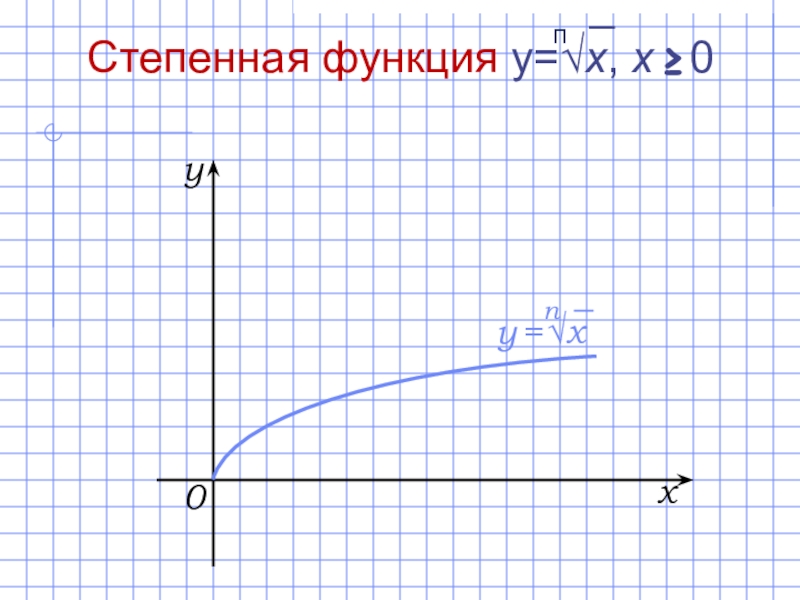
- 23. D(f) = [0; +∞).E(f) = [0; +∞).
- 24. 0xy
- 25. D(f) = (–∞; +∞).E(f) = (–∞; +∞).
- 26. xy0
Слайд 2Понятие функции
Если каждому значению х из некоторого множества чисел поставлено в
y = f(x)
При этом х называют независимой переменной или аргументом,
а у – зависимой переменной или функцией.
Слайд 3Область определения и
множество значений функции
Областью определения функции называют множество всех
Обозначается D(y)
Множество значений (или область значений) функции – это множество всех значений переменной у.
Обозначается E(y)
Слайд 4Свойства функций:
монотонность
Функцию y = f(x) называют возрастающей на множестве Х,
Функцию y = f(x) называют убывающей на множестве Х, если для любых двух элементов из этого множества, таких, что х1 < x2, выполняется условие f(x1) > f(x2).
(Функцию называют возрастающей, если большему значению аргумента соответствует большее значение функции)
(Функцию называют убывающей, если большему значению аргумента соответствует меньшее значение функции)
Слайд 5Свойства функций:
ограниченность
Функцию y = f(x) называют ограниченной снизу на множестве
f(x) > m.
Функцию y = f(x) называют ограниченной сверху на множестве Х, если существует число M, такое, что для любого значения х ∊ Х, выполняется неравенство
f(x) < M.
Если функция ограничена и снизу и сверху, то ее называют ограниченной
Слайд 6Свойства функций:
наибольшее и наименьшее значения функции
Число m называют наименьшим значением функции
существует число хо ∊ Х такое, что f(хo) = m;
для любого значения х ∊ Х выполняется неравенство
f(x) ≥ f(xo).
Число М называют наибольшим значением функции y = f(x) на множестве Х, если:
существует число хо ∊ Х такое, что f(хo) = М;
для любого значения х ∊ Х выполняется неравенство
f(x) ≤ f(xo).
Слайд 7Свойства функций:
четность или нечетность
Функцию y = f(x), х ∊ Х
Функцию y = f(x), х ∊ Х называют нечетной, если для любого значения х из множества Х выполняется равенство f(–x) = – f(x).
График четной функции симметричен относительно оси ординат.
График нечетной функции симметричен относительно начала координат.
Слайд 8Свойства функций:
точки экстремума
Точку хо называют точкой максимума функции y = f(x),
f(x) < f(xo).
Точку хо называют точкой минимума функции y = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки хо) выполняется неравенство
f(x) > f(xo).
Точки максимума и минимума объединяют общим названием – точки экстремума
Слайд 9Свойства функций:
периодичность
Говорят, что функция y = f(x), х ∊ Х
f(x – Т) = f(x) = f(x + T).
Функцию, имеющую отличный от нуля период называют периодической.
Если функция y = f(x), х ∊ Х имеет период Т, то любое число, кратное Т (т.е. число вида kT, k ∊ Z), также является ее периодом.
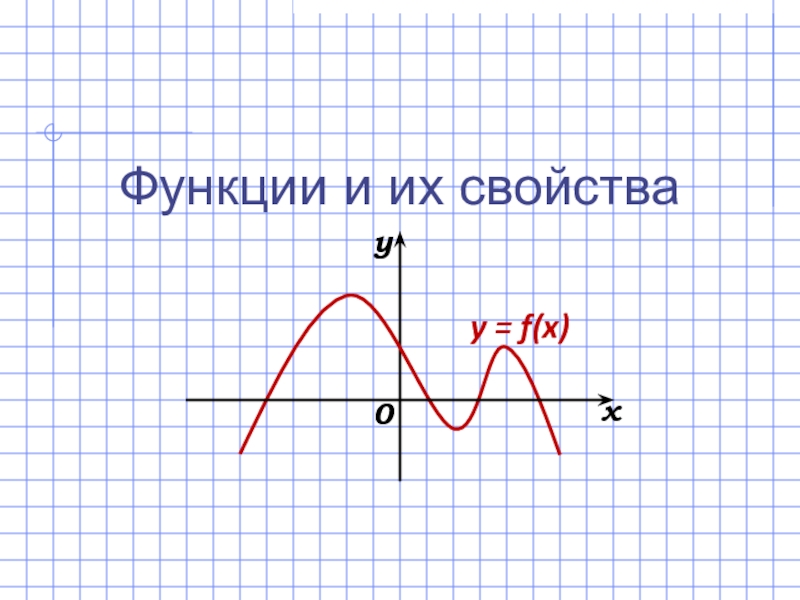
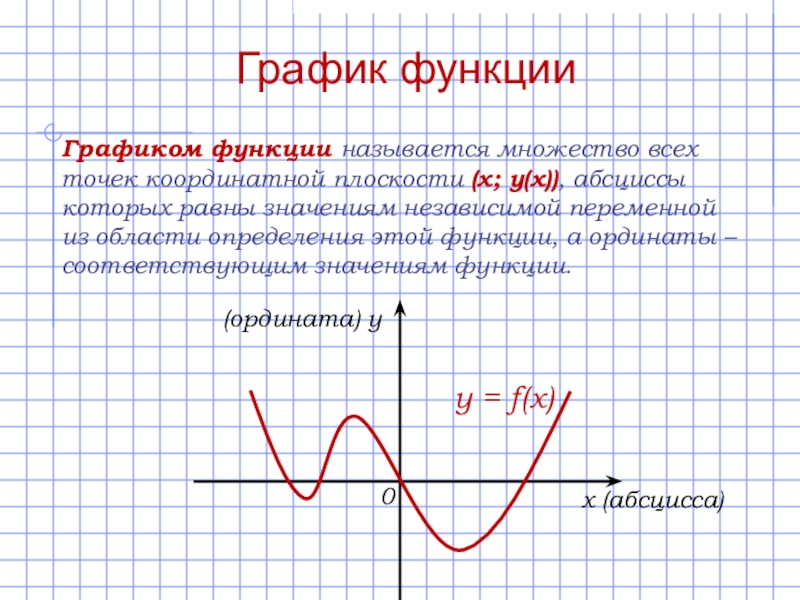
Слайд 10График функции
Графиком функции называется множество всех точек координатной плоскости (х; у(х)),
x (абсцисса)
(ордината) y
y = f(x)
0
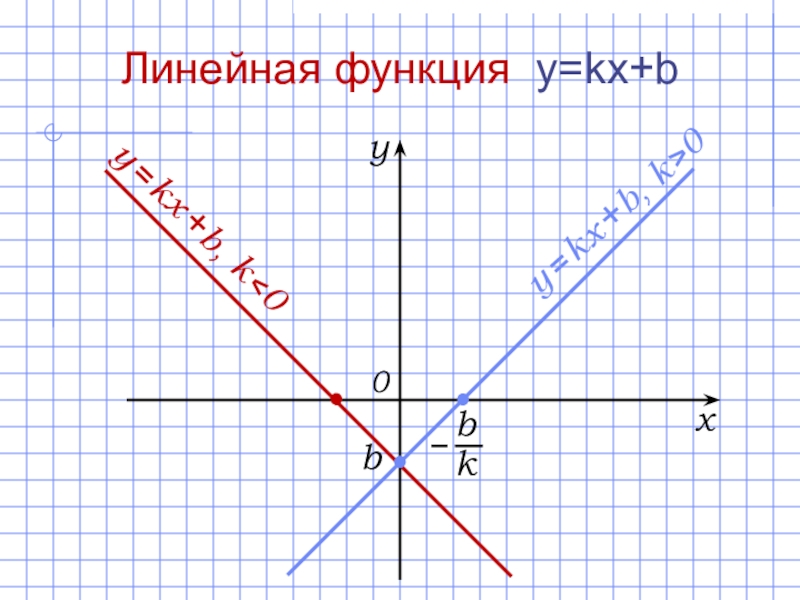
Слайд 12Линейная функция y=kx+b
Свойства линейной функции y = kx + b:
D(f) =
E(f) = (–∞; +∞).
Если b = 0, то функция нечетная.
а) Нули функции: (– b/k; 0);
б) точка пересечения с Оу: (0; b).
а) возрастает, если k > 0;
б) убывает, если k < 0.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–∞; +∞).
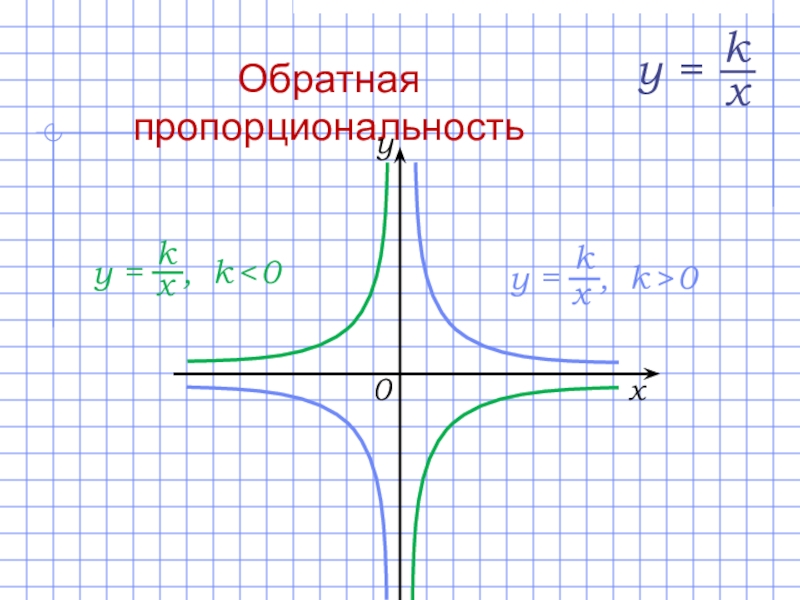
Слайд 14Свойства функции y = k/x:
D(f) = (–∞; 0) ∪ (0; +∞).
E(f)
Функция нечетная.
а) Нули функции: нет;
б) точка пересечения с Оу: нет.
а) если k < 0, то (–∞; 0) и (0; +∞) – промежутки возрастания функции;
б) если k > 0, то (–∞; 0) и (0; +∞) – промежутки убывания функции.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на каждом из промежутков
(–∞; 0) и (0; +∞).
Обратная пропорциональность
Слайд 16Свойства функции y = kx2 при k > 0:
D(f) = (–∞;
E(f) = [0; +∞).
Функция четная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
а) [0; +∞) – промежуток возрастания функции;
б) (–∞; 0] – промежуток убывания функции.
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве (–∞; +∞).
Выпукла вниз.
Квадратичная функция y=kx2
Слайд 17Свойства функции y = kx2 при k < 0:
D(f) = (–∞;
E(f) = (–∞; 0].
Функция четная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
а) [0; +∞) – промежуток убывания функции;
б) (–∞; 0] – промежуток возрастания функции.
Ограничена сверху, не ограничена снизу.
а) унаиб. = 0;
б) унаим. – не существует.
Непрерывна на множестве (–∞; +∞).
Выпукла вверх.
Квадратичная функция y=kx2
Слайд 19
D(f) = [0; +∞).
E(f) = [0; +∞).
Функция ни четная, ни
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
[0; +∞) – промежуток возрастания функции.
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; +∞).
Выпукла вверх.
Слайд 21Свойства кубической функции y = x3:
D(f) = (–∞; +∞).
E(f) = (–∞;
Функция нечетная.
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
Возрастает на множестве (–∞; +∞).
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–∞; +∞).
Кубическая функция y=x3
Слайд 23
D(f) = [0; +∞).
E(f) = [0; +∞).
Функция ни четная, ни
а) Нули функции: (0; 0);
б) точка пересечения с Оу: (0; 0).
[0; +∞) – промежуток возрастания функции.
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; +∞).
Выпукла вверх.
Слайд 25
D(f) = (–∞; +∞).
E(f) = (–∞; +∞).
Функция нечетная.
а) Нули функции:
б) точка пересечения с Оу: (0; 0).
Возрастает на множестве (–∞; +∞).
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего, ни наименьшего значений.
Функция непрерывна на множестве (–∞; +∞).












![Свойства функции Свойства функции y = kx2 при k < 0:D(f) = (–∞; Свойства функции y = kx2 при k < 0:D(f) = (–∞; +∞).E(f) = (–∞; 0].Функция четная.а) Нули](/img/thumbs/bf9580dc50f6522559406a229e27845b-800x.jpg)