- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Способы решения квадратных уравнений
Содержание
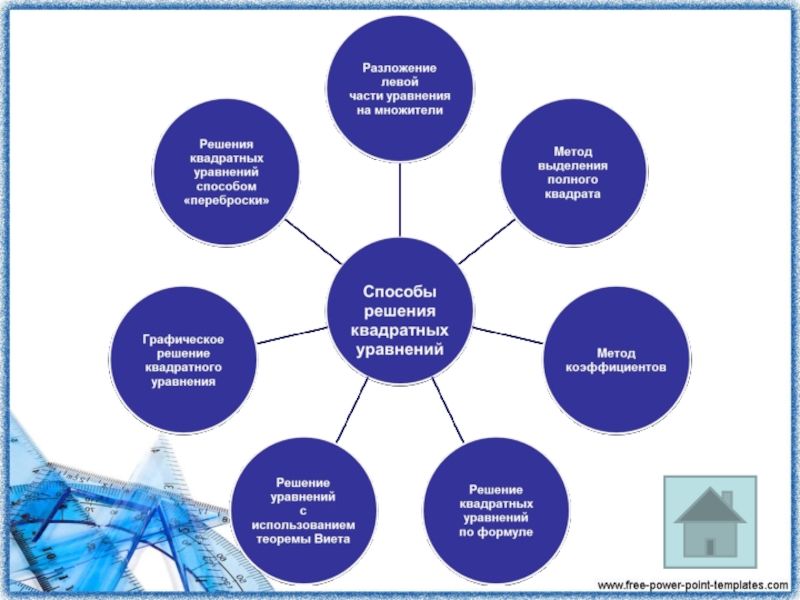
- 1. Способы решения квадратных уравнений
- 2. Цель урока:познакомиться с различными способами решения квадратных
- 3. Из истории о квадратных уравнениях Необходимость решать уравнения
- 4. Индийский ученый Брахмагупта (VII в.), изложил общее
- 5. В алгебраическом трактате Аль -Хорезми дается классификация
- 6. Итальянские математики Тарталья, Кардано, Бомбелли среди первых
- 7. Квадратное уравнение.Квадратным уравнением называется уравнение вида ax²+bх+с=0,
- 8. Слайд 8
- 9. Решение квадратных уравнений по формуле Примеры для решения: 2х2-5х+2=0, х2-10х-24=0.
- 10. Разложение левой части уравнения на множителиВынесение общего
- 11. Метод выделения полного квадрата Данный метод заключается в
- 12. Метод коэффициентов Пусть дано квадратное уравнение ах2 +
- 13. Решение уравнений с помощью теоремы Виета Как известно,
- 14. б) Если свободный член q приведенного уравнения (1) отрицателен
- 15. Графический метод решения квадратного уравненияПреобразуем уравнение х2
- 16. Решение квадратных уравнений методом «переброски» При этом способе
- 17. Домашнее задание Подобрать по 2 уравнения к каждому из предложенных способов и решить их.
Слайд 1Способы решения квадратных уравнений
Подготовила Шиловская Ольга Васильевна
Преподаватель ГАПОУ АО КЛТТ
Слайд 2Цель урока:
познакомиться с различными способами решения квадратных уравнений.
Задачи урока:
Изучить различные
Оборудование урока:
Компьютер;
мультимедийный проектор;
презентация к уроку.
Слайд 3Из истории о квадратных уравнениях
Необходимость решать уравнения не только первой, но
Слайд 4Индийский ученый Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений,
ах2 + bх = с, а > 0
В уравнении коэффициенты, кроме а, могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.
Формулы решения квадратных уравнений были впервые изложены итальянским математиком Леонардо Фибоначчи (XIIIв.). х² + bх = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь
в 1544 г.
Слайд 5 В алгебраическом трактате Аль -Хорезми дается классификация линейных и квадратных уравнений.
«Квадраты равны корням», т. е. ах² = bх.
2) «Квадраты равны числу», т. е. ах² = с.
3) «Корни равны числу», т. е. ах² = с.
4) «Квадраты и числа равны корням», т. е. ах² + с = bх.
5) «Квадраты и корни равны числу», т. е. ах² + bх = с.
6) «Корни и числа равны квадратам», т. е. bх + с = ах².
Слайд 6
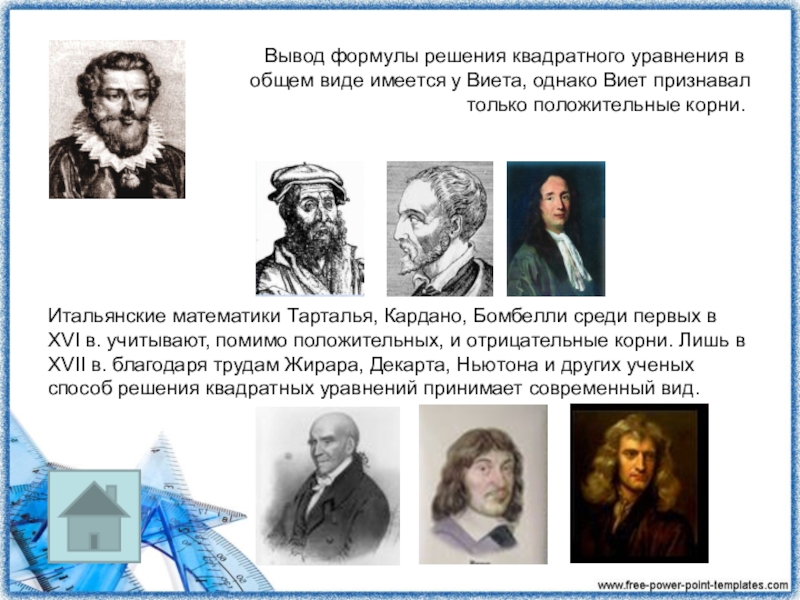
Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают,
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни.
Слайд 7Квадратное уравнение.
Квадратным уравнением называется уравнение вида ax²+bх+с=0, где х – переменная,
Числа a, b, с – коэффициенты квадратного уравнения. Число a – первый коэффициент, b – второй коэффициент, с – свободный член.
Если в квадратном уравнении ax²+bx+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент a=1 называется приведенным квадратным уравнением.
Слайд 10Разложение левой части уравнения на множители
Вынесение общего множителя за скобки;
Использование формул
Способ группировки.
Например: Решить уравнение 9x²-6x+1=0.
Разложим левую часть на множители, используя формулы сокращенного умножения (квадрат разности двух чисел или выражений).
Получим: 9x²-6x+1=(3x-1)²=(3x-1)(3x-1)=0.
Так как произведение равно нулю, то, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 1∕3. Это означает, что число -1∕3 является корнем уравнения 9x²-6x+1=0.
Подобный пример: х2 + 10х - 24 = 0.
Слайд 11Метод выделения полного квадрата
Данный метод заключается в приведении квадратного уравнения общего
Например: Решить уравнение x²+2x-15=0.
Разложим левую часть на множители, используя формулы сокращенного умножения (квадрат разности).
Получим: x²+2x-15=x²+2x+1-1-15= (x+1)²-16= 0.
Отсюда, (x+1)²=16. Следовательно, х + 1 = 4, или х + 1 = -4
х1 = 3, х2 = -5.
Подобный пример: х2 + 6х - 7 = 0.
Слайд 12Метод коэффициентов
Пусть дано квадратное уравнение ах2 + bх + с =
Если, а+ b + с = 0 , то
Если b = a + c, то
Например: 1) 2x²+3x-5=0.
Так как a+b+c=2+3+(-5)=0, то
2) -x²+7x+8=0.
Так как b=a+c, т. е. 7=-1+8, то
Слайд 13Решение уравнений с помощью теоремы Виета
Как известно, приведенное квадратное уравнение имеет
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x2 + 8x + 7 = 0; x1 = - 7 и x2 = - 1, так как q = 7 > 0 и p= 8 > 0.
Слайд 14б) Если свободный член q приведенного уравнения (1) отрицателен
(q < 0), то
Например,
x2 + 4x – 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.
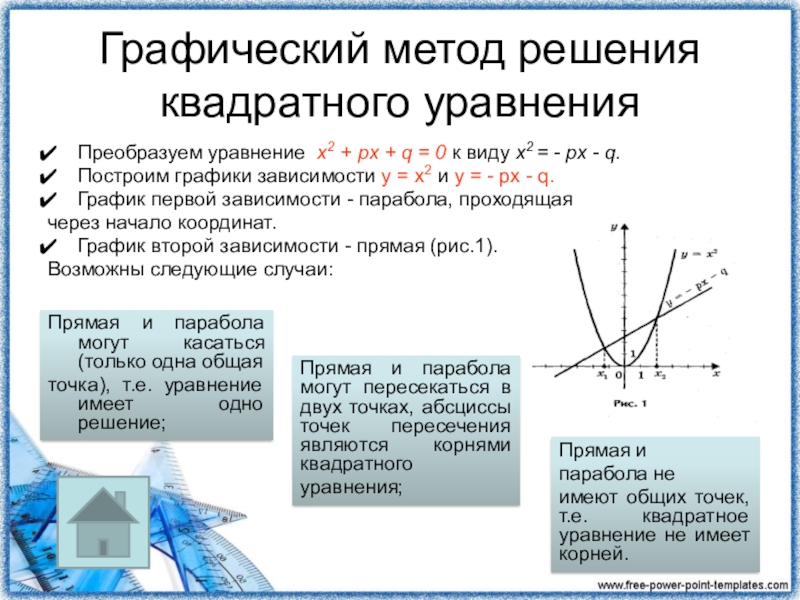
Слайд 15Графический метод решения квадратного уравнения
Преобразуем уравнение х2 + px + q
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая
через начало координат.
График второй зависимости - прямая (рис.1).
Возможны следующие случаи:
Прямая и парабола могут касаться (только одна общая
точка), т.е. уравнение имеет одно решение;
Прямая и
парабола не
имеют общих точек, т.е. квадратное уравнение не имеет корней.
Прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного
уравнения;
Слайд 16Решение квадратных уравнений методом «переброски»
При этом способе коэффициент а умножается на
Решим уравнение 6x²+x-1=0.
«Перебросим» коэффициент 6 к свободному члену, в результате получим уравнение
у2 +у -1 = 0.
Согласно теореме Виета у₁ = -3, у₂ = 2, то х1 = -3/6=-1∕2, х₂ = 2/6=1∕3.
Ответ: -1/2 и 1/3.
Подобный пример: 2х2 – 11х + 15 = 0.