- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Способы нахождения приближенного значения числа пи
Содержание
- 1. Способы нахождения приближенного значения числа пи
- 2. Изучить историю происхождения числа π, как самого
- 3. Число π («пи») определяется как отношение длины
- 4. 1) длина окружности пропорциональна ее диаметру;2) площадь
- 5. Такое приближение использовалось, например, в Древнем Вавилоне
- 6. от площади квадрата, описанного вокруг круга, отнимались
- 7. для вычисления площади круга использовалось правило S
- 8. У древнегреческих математиков с их превалирующим интересом
- 9. Изучая задачу о квадратуре круга, Гиппократ Хиосский
- 10. Древнейшие известные попытки вычисления собственно квадратуры круга
- 11. Архимед доказал, что площадь круга равна половине
- 12. Клавдий Птолемей, использовав правильный 720-угольник, нашел, что
- 13. Далее метод вписанных и описанных многоугольников уступил место
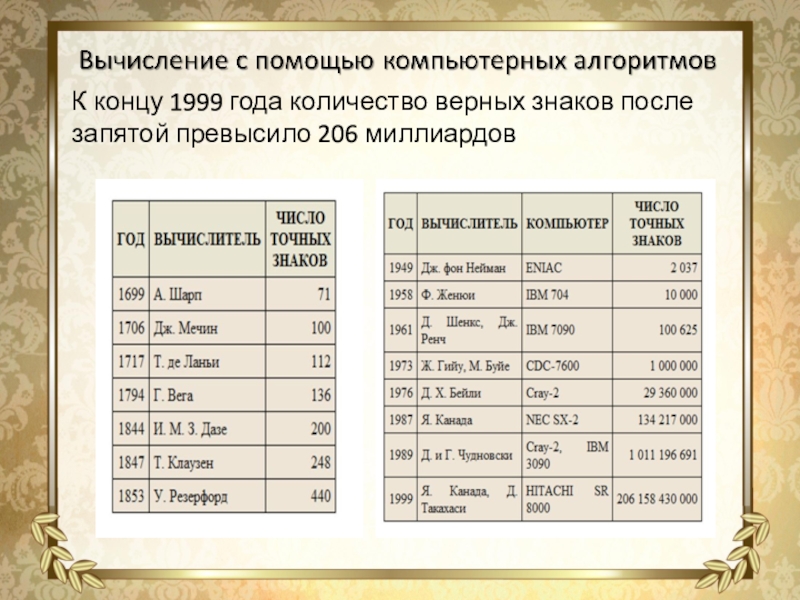
- 14. К концу 1999 года количество верных знаков после запятой превысило 206 миллиардов
- 15. На листе картона начертить квадрат. Вписать в
- 16. Это фактически метод статистических испытаний. Свое экзотическое
- 17. Мы изучили историю происхождения числа π Ознакомились
- 18. - Значение числа π в современном мире
Слайд 2Изучить историю происхождения числа π, как самого известного в мире иррационального
Цель работы
Слайд 3Число π («пи») определяется как отношение длины окружности C к ее
Другая известная формула, в которой встречается π, – формула площади круга S = πr2, или S = πd2/4.
В принципе π можно было бы определить как отношение площади круга к квадрату радиуса.
Приближения числа Пи
Слайд 41) длина окружности пропорциональна ее диаметру;
2) площадь круга пропорциональная квадрату радиуса;
3)
Десятичная дробь, выражающая число π, бесконечна, хотя можно вычислить различные конечные дроби – десятичные приближения для π. Наиболее популярное приближение – с точностью до сотых: π ≈ 3,14.
За этими формулами скрываются
три нетривиальных математических факта:
Слайд 5
Такое приближение использовалось, например, в Древнем Вавилоне в III–II вв. до
длину окружности находили по правилу, которое в современных обозначениях можно записать
C = 3d,
площадь круга находили по правилу S = C2/12.
Значение π = 3 использовалось и древними иудеями, где упоминалось в библейских текстах
Самое простое приближение для π
полагает его равным 3
Слайд 6от площади квадрата, описанного вокруг круга, отнимались площади треугольников с длиной
Геометрические приближения площади круга,
Древний Вавилон :
Слайд 7для вычисления площади круга использовалось правило S = (8d / 9)2,
Геометрические приближения площади круга,
Древний Египет :
Слайд 8У древнегреческих математиков с их превалирующим интересом к геометрическим построениям и
Задача о квадратуре круга
Слайд 9Изучая задачу о квадратуре круга, Гиппократ Хиосский (V в. До н.
Задача о квадратуре круга
и вычисление числа π
Слайд 10Древнейшие известные попытки вычисления собственно квадратуры круга принадлежат Антифонту и Бризону
Антифонт последовательно вписывал в круг правильные многоугольники, каждый раз удваивая количество сторон, и полагал, что в конце концов многоугольник совпадет с окружностью. Бризон строил два квадрата – вписанный в окружность и описанный вокруг нее – и считал, что площадь квадрата, лежащего между ними, равна площади круга.
Задача о квадратуре круга
и вычисление числа π
Слайд 11Архимед доказал, что площадь круга равна половине произведения длины окружности на
или, в десятичных дробях, 3,1409... < π < 3,1428... (подлинное значение π = 3,14159...).
Таким образом, он не только нашел приближенные значения π, но и оценил точность этих приближений. Уже найденная Архимедом верхняя оценка, равная 22/7, дает приближение π с точностью 0,04 %. Эту дробь часто называют «архимедовым числом».
«Архимедово число»
Слайд 12Клавдий Птолемей, использовав правильный 720-угольник, нашел, что π ≈ 377/120, что
В начале XVII в. профессор математических и военных наук Лейденского университета Лудольф ван Цейлен [4] довел количество точных знаков (после запятой) числа π до 35. Современники называли найденное им приближение π «числом Лудольфа». Эти знаки он завещал выбить на надгробном камне. Интересно, что, поскольку в то время привычная нам позиционная запись десятичных дробей еще не вполне прижилась, на надгробии было написано не 3,14159265358979323846264338327960288, а
Результаты вычисления числа «пи» различными учеными
Слайд 13 Далее метод вписанных и описанных
многоугольников уступил место
новым методам, разработанным
с
анализа – использованию
бесконечных сумм, которые
дают приближенные значения числа π нужной точности.
Рекорд для XIX в. поставил Уильям Шенкс, нашедший в результате 527знаков после запятой.
Компьютеры позволили существенно увеличить количество точных цифр в десятичном разложении π, причем, если раньше вычислители тратили на них многие годы, то теперь компьютеры справлялись с этим менее чем за день работы.
Вычисление с помощью математического анализа
Слайд 15На листе картона начертить квадрат. Вписать в него круг. Вырезать квадрат.
Естественно, что в данном случае приближенное значение зависит от точности взвешивания. Если взвешиваемые картонные фигуры будут довольно большими, то возможно даже на обычных весах получить такие значения масс, которые обеспечат приближение числа с точностью до 0,1.
Вычисление опытным путём
с помощью взвешивания
Слайд 16Это фактически метод статистических испытаний. Свое экзотическое название он получил от
Для опыта приготовим кусок картона, нарисуем на нем квадрат и впишем в квадрат четверть круга. Если такой чертеж некоторое время подержать под дождем, то на его поверхности останутся следы капель. Подсчитаем число следов внутри квадрата и внутри четверти круга. Очевидно, что их отношение будет приближенно равно отношению площадей этих фигур, так как попадание капель в различные места чертежа равновероятно.
Вычисление опытным путём: метод Монте-Карло
Слайд 17
Мы изучили историю происхождения числа π
Ознакомились с учёными, находившими его
Рассмотрели популярные методы вычисления π:
- метод геометрического приближения;
- метод квадратуры круга;
- метод вписанных и описанных правильных многоугольников;
- метод математического анализа;
- метод взвешивания;
- метод Монте- Карло.
Таким образом для достижения поставленной
цели были выполнены следующие задачи:
Слайд 18- Значение числа π в современном мире представляет собой не только
- С числом π связано много интересных фактов, поэтому оно вызывает интерес к изучению;
- История числа π это череда усилий величайших умов человечества по уточнению его знаков и поисков алгоритмов для их нахождения.
Заключение