- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение типовых заданий ЕГЭ второй части задание 15-2
Содержание
- 1. Решение типовых заданий ЕГЭ второй части задание 15-2
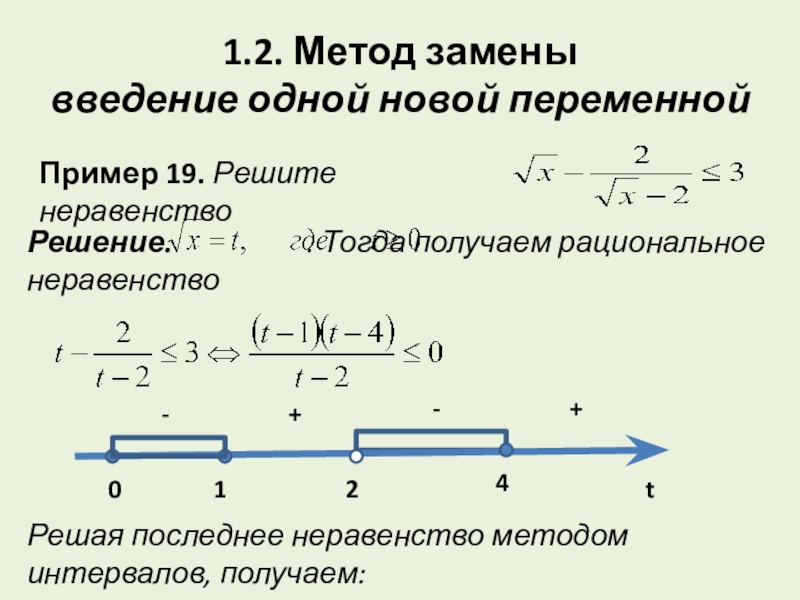
- 2. 1.2. Метод замены введение одной новой переменнойПример
- 3. Пример 20. (МИОО, 2009). Решите неравенствоРешение. Пусть , тогда получаем систему неравенств
- 4. Выполняя обратную замену, получаемОтсюда получаем
- 5. Пример 21. (ЕГЭ 2010). Решите неравенствоРешение. В
- 6. Отсюда С учетом последнего неравенства, запишем полученную
- 7. Решим последнее неравенство:С учетом ограничения на t
- 8. Пример 22. (МФТИ, 2009). Решите неравенствоРешение. Область
- 9. Полагая , получим неравенствоИспользуем геометрический способ решения последнего
- 10. Аналогично искомые точки находятся слева от точки
- 11. введение двух новых переменныхПример 23. (Тренировочная работа
- 12. Заметим, что 2x2 - x + 5
- 13. тригонометрическая подстановкаЕсли область определения данного неравенства совпадает
- 14. Пример 23. Решите неравенствоРешение. Для решения неравенства
- 15. Уравнение примет вид cost - 4sin 3
- 16. то в силу возрастания функции y =
- 17. Замечание. Если учесть, чтото ответ можно записать в следующем виде:
- 18. 1.3. Разбиение области определения неравенства на подмножестваРазбиение
- 19. возрастания функции y = 2 t ).
- 20. Объединим решения, полученные в первом и втором
- 21. Рассмотрим два случая.1. Пусть x >2 .Тогда
- 22. Так как уравнение x2 - 2x +
- 23. Решение. ОДЗ неизвестной данного неравенства находим из
- 24. Поскольку при x -3 верно
- 25. следует at bt . Поэтому
- 26. Значит исходное неравенство на рассматриваемом промежутке выполняетсятолько
- 27. Используемая литература:Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
Слайд 1(типовые задания С3) - 1
Методы решения неравенств
с одной переменной
Методическая разработка Амачкиной
МОУ СОШ №12,
г. Балашиха, Московской области.
Слайд 21.2. Метод замены
введение одной новой переменной
Пример 19. Решите неравенство
Решение. . Тогда получаем
Решая последнее неравенство методом интервалов, получаем:
Слайд 3Пример 20. (МИОО, 2009). Решите неравенство
Решение. Пусть , тогда получаем систему неравенств
Слайд 5Пример 21. (ЕГЭ 2010). Решите неравенство
Решение. В соответствии с определением логарифма,
Сделаем замену 7 = t . Так как неравенство выполняется при всех x , то по свойству степени с основанием больше единицы получаем
Слайд 6Отсюда С учетом последнего неравенства, запишем полученную выше систему
Исходное неравенство с
Используя свойство логарифма (при допустимых значениях переменной сумма логарифмов с одинаковым основанием равна логарифму произведения), получим
Слайд 7Решим последнее неравенство:
С учетом ограничения на t получаем 0 < t
Выполнив обратную замену, имеем 7 -x2 < 7 -16
Отсюда x2>16
Слайд 8Пример 22. (МФТИ, 2009). Решите неравенство
Решение. Область определения данного неравенства определяется
Так как при допустимых значениях x справедливо
Равенство то, сделав замену
log 2 (x +1) = t , получим неравенство
Слайд 9Полагая , получим неравенство
Используем геометрический способ решения последнего неравенства (см. раздел «Геометрические
Слайд 10Аналогично искомые точки находятся слева от точки –2 на расстоянии меньше
Последнее неравенство равносильно совокупности двух неравенств
Слайд 11введение двух новых переменных
Пример 23. (Тренировочная работа МИОО, ЕГЭ 2011). Решите
Решение. Входящие в неравенство выражения имеют смысл при
При всех остальных x неравенство равносильно следующему
Слайд 12Заметим, что 2x2 - x + 5 = (x2 - 4x
Пусть x2 - 4x + 3 = u и x2 + 3x + 2 = v .
Тогда последнее неравенство примет вид
Отсюда следует, что u =v . Выполняя обратную замену,
получаем
Слайд 13тригонометрическая подстановка
Если область определения данного неравенства совпадает с областью значений тригонометрической
замен:
для неравенств, содержащих выражения
для неравенств, содержащих выражения
Слайд 14Пример 23. Решите неравенство
Решение. Для решения неравенства используем метод интервалов.
Так как
Слайд 15Уравнение примет вид cost - 4sin 3 t + 3sin t
сos t + sin 3t = 0 . Далее имеем
Поскольку промежутку принадлежат три
Числа , то корнями рассматриваемого уравнения являются числа ,
Слайд 16то в силу возрастания функции y = sin t на промежутке
имеем
4.
Так как f (x) непрерывна, как сумма непрерывных функций, и f (0) > 0 , то получаем, что f (x) 0 при всех
значениях
Слайд 181.3. Разбиение области определения
неравенства на подмножества
Разбиение ОДЗ неизвестной неравенства на промежутки
Пример 25. Решите неравенство
Решение. Данное неравенство определено при всех значениях х. Рассмотрим два случая.
Пусть x 0 , тогда неравенство примет следующий
вид: (в силу
Слайд 19возрастания функции y = 2 t ).
2. Если x >
С учетом условия x < 0 получаем, что является решением неравенства на рассматриваемом промежутке, поскольку
Слайд 20Объединим решения, полученные в первом и втором случаях.
Пример 26. Решите неравенство
Решение.
Слайд 21Рассмотрим два случая.
1. Пусть x >2 .
Тогда неравенство примет следующий вид:
log2(
2log2 (x-2) – log2 (x+2)>1.
Отсюда
(x - 2)2 > 2(x + 2) или x(x - 6) > 0 .
С учетом условия x > 2 получаем x > 6.
2. Пусть x <-2 .
В этом случае неравенство примет следующий вид:
log2(2 -x ) + log2(-x-2) - 3log2(-x-2) + 3log2(2-x ) >2 или
2log2 (2-x ) – log2 ( -x-2) >1.
Отсюда
(2 - x)2 > 2(-x - 2) или x2 - 2x + 8>0 .
Слайд 22Так как уравнение x2 - 2x + 8 = 0 не
В этом случае все значения x < -2 являются решениями неравенства.
Объединим полученные решения.
Ответ: x < -2 или x > 6 .
Пример 27. Решите неравенство
Слайд 23Решение. ОДЗ неизвестной данного неравенства находим из условия x2 - 2x
Рассмотрим исходное неравенство на двух промежутках: 1) x -3 и 2) x 5 .
1. При x -3 исходное неравенство равносильно неравенству
Слайд 24Поскольку при x -3 верно каждое из неравенств:
то
2. Пусть x 5 . Заметим, что неравенство
справедливо на всем этом промежутке. Это следует из его решения
В силу возрастания функции
Слайд 25следует at bt . Поэтому имеем
причем равенство достигается при
Отсюда получаем
Слайд 26Значит исходное неравенство на рассматриваемом промежутке выполняется
только при x = 5
Объединим решения, полученные в первом и втором случаях.