- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Сумма геометрической прогрессии
Содержание
- 1. Презентация Сумма геометрической прогрессии
- 2. Ответ:321
- 3. РешениеB2=14В3=28В4=56S = 7+14+28+56=105Найдите сумму 10 первых членов
- 4. Тема урока Сумма n первых членов геометрической прогрессии
- 5. Легенда о шахматах
- 6. Сколько зёрен?S=1+2+22+23+…+262+263Умножим обе части записанного равенства на
- 7. 184467447370955161518 квинтильонов 446 квадрильонов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615 зёрен
- 8. Вывод формулыSn =b₁+b2+…+bn-1+bn
- 9. Формула
- 10. Работа по учебнику№648(а) , №649(а, в) , №650(а) Стр. 161
- 11. Задача о бактерияхВ благоприятных условиях бактерии размножаются
- 12. Самостоятельная работа1) Найдите сумму пяти первых членов
- 13. Домашнее заданиеВыучить формулы; №648(б) , №649(б, г)
- 14. Задача о богачеБогач вернулся домой радостный: у
- 15. Спасибо за урок!
- 16. К сведениюГеометрическая прогрессия называется бесконечно убывающей, если
Ответ:321
Слайд 6Сколько зёрен?
S=1+2+22+23+…+262+263
Умножим обе части записанного равенства на знаменатель прогрессии, получим:
2S=2+22+23+…+262+263+264
Вычтем почленно
из второго равенства первое и проведём упрощение:
2S-S=(2+22+23+…+262+263+264)-(1+2+22+23+…+262+263)
S=264-1
2S-S=(2+22+23+…+262+263+264)-(1+2+22+23+…+262+263)
S=264-1
Слайд 71844674473709551615
18 квинтильонов 446 квадрильонов 744 триллиона 73 биллиона 709 миллионов 551
тысяча 615 зёрен
Слайд 8Вывод формулы
Sn =b₁+b2+…+bn-1+bn
(1)
Умножим обе части этого равенства на q:
Snq=b₁q + b2q+b3q+…+bn-1q +bnq.
Учитывая, что b₁q=b2, b2q= b3, b3q=b4 ,…, bn-1q=bn , получим
Sn q =b2+ b3 +b4 +…+bn-1+ bn + bnq (2)
Вычтем почленно из равенства (2) равенство (1) и приведём подобные члены:
Snq –Sn =(b2+b3+ …+bn-1+bn + bnq)-(b₁+b2+…+bn-1+bn)= bnq- b₁
Sn(q –1)= bnq- b₁ Отсюда следует, что при q≠1
Умножим обе части этого равенства на q:
Snq=b₁q + b2q+b3q+…+bn-1q +bnq.
Учитывая, что b₁q=b2, b2q= b3, b3q=b4 ,…, bn-1q=bn , получим
Sn q =b2+ b3 +b4 +…+bn-1+ bn + bnq (2)
Вычтем почленно из равенства (2) равенство (1) и приведём подобные члены:
Snq –Sn =(b2+b3+ …+bn-1+bn + bnq)-(b₁+b2+…+bn-1+bn)= bnq- b₁
Sn(q –1)= bnq- b₁ Отсюда следует, что при q≠1
Пусть дана геометрическая прогрессия (bn). Обозначим сумму n первых членов через Sn:
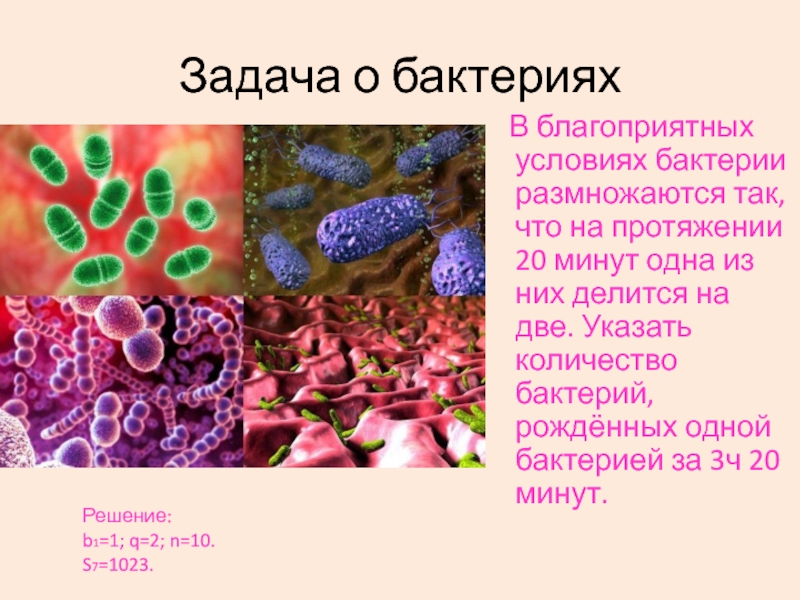
Слайд 11Задача о бактериях
В благоприятных условиях бактерии размножаются так, что на протяжении
20 минут одна из них делится на две. Указать количество бактерий, рождённых одной бактерией за 3ч 20 минут.
Решение:
b1=1; q=2; n=10. S7=1023.
Слайд 12Самостоятельная работа
1) Найдите сумму пяти первых членов геометрической прогрессии, если первый
член равен 2, а знаменатель прогрессии равен 0,5
2) Найдите сумму пяти первых членов геометрической прогрессии 2; 6;…
Ответ: 1) 3,875 2) 242
2) Найдите сумму пяти первых членов геометрической прогрессии 2; 6;…
Ответ: 1) 3,875 2) 242
Слайд 13Домашнее задание
Выучить формулы; №648(б) , №649(б, г) , №650(б). Продолжить выполнение
проектной работы по теме «Прогрессии»
На повторение: №659, 660
Для желающих: 1)Изобразить героев легенды о шахматной доске.
2) Задача о богаче.
На повторение: №659, 660
Для желающих: 1)Изобразить героев легенды о шахматной доске.
2) Задача о богаче.
Слайд 14Задача о богаче
Богач вернулся домой радостный: у него была счастливая встреча,
сулившая большие выгоды. Повстречался ему в пути незнакомец, предложивший сделку: «Я буду целый месяц приносить тебе ежедневно по 100000 р., но недаром. В первый день ты уплатишь мне 1 к., во второй – 2 к., в третий – 4 к. и так целый месяц» Богач согласился. Кто прогадал – богач или незнакомец?
Слайд 16К сведению
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше
единицы.
Суммой бесконечно убывающей геометрической прогрессии называют число,к которому стремится сумма её первых n членов при n→∞.
Суммой бесконечно убывающей геометрической прогрессии называют число,к которому стремится сумма её первых n членов при n→∞.