- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задания на смекалку. ЕГЭ по математике. Базовый уровень. Задания № 20
Содержание
- 1. Презентация по математике Задания на смекалку. ЕГЭ по математике. Базовый уровень. Задания № 20
- 2. Задача 1На прилавке цветочного магазина стоят 3
- 3. Решение задачи 1Из первого условия следует, что
- 4. Задача 3Маша и Медведь съели 160 печений и
- 5. Решение задачи 3Медведь съел свою половину банки
- 6. Задача 5Если бы каждый из двух сомножителей
- 7. Решение задачи 5Пусть первый сомножитель равен a,
- 8. Задача 7Агрофирма закупает куриные яйца в двух
- 9. Решение задачи 7Х – вероятность того, что
- 10. Задача 9Из десяти стран семь подписали договор
- 11. Решение задачи 9Две страны подписывают один общий
- 12. Задача 10Хозяин договорился с рабочими, что они
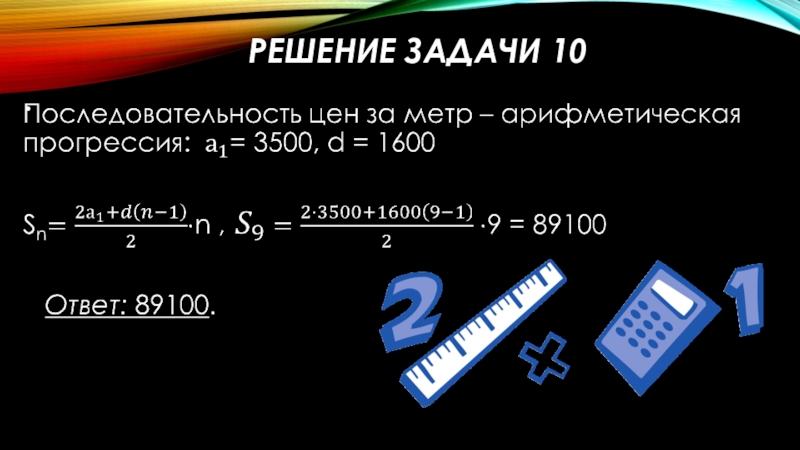
- 13. Решение задачи 10
- 14. Задача 11Хозяин договорился с рабочими, что они
- 15. Решение задачи 11
- 16. Задача 12По эмпирическому закону Мура среднее число
- 17. Решение задачи 12
- 18. Задача 13Тренер посоветовал Андрею в первый день
- 19. Решение задачи 13
- 20. Задача 14В результате паводка котлован заполнился водой
- 21. Решение задачи 142м=2× 100 = 200 см
- 22. Задача 15Нефтяная компания бурит скважину для добычи
- 23. Решение задачи 15 Учитывая заливание скважины, в
- 24. Задача 16Ящики двух видов, имеющие одинаковую ширину
- 25. Решение задачи 16 Так как надо найти
- 26. Задача 17В таблице три столбца и несколько
- 27. Решение задачи 17119 + 125 + 133
- 28. Задача 18Список заданий викторины состоял из 36
- 29. Решение задачи 18 1 способ: Балл
- 30. Задача 19Список заданий викторины состоял из 25
- 31. Задача 21Врач прописал пациенту принимать лекарство по
- 32. Решение задачи 21
- 33. Задача 22Врач прописал пациенту принимать лекарство по
- 34. Решение задачи 22
- 35. Задача 23В меню ресторана имеется 6 видов
- 36. Решение задачи 23Салат можно выбрать 6 способами,
- 37. Задача 24Группа туристов преодолела горный перевал. Первый
- 38. Решение задачи 2450+65+80+95+10+60+50+40+30+20+10=290+220=510 мин, 510:60=8,5 час Ответ: 8,5
- 39. Задача 25На кольцевой дороге расположены четыре бензоколонки:
- 40. Решение задачи 25Расположим А, В,С,D вдоль кольцевой
- 41. Задача 26На кольцевой дороге расположены четыре бензоколонки:
- 42. Решение задачи 26Расположим А, В,С,D вдоль кольцевой
- 43. Задача 27На кольцевой дороге расположены четыре бензоколонки:
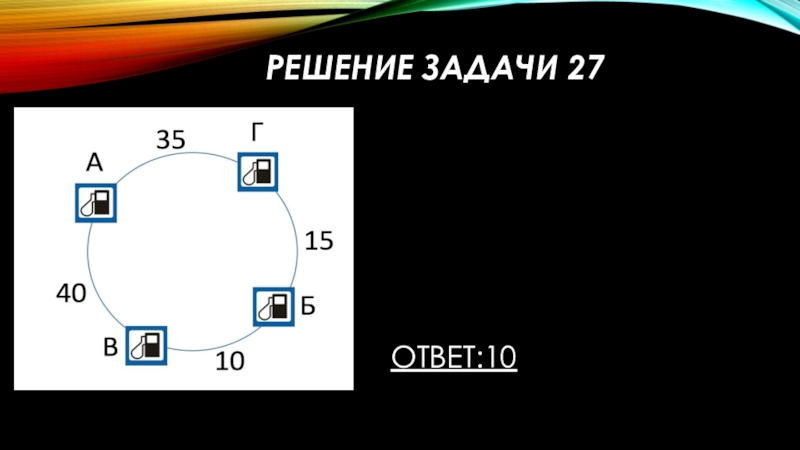
- 44. Решение задачи 27Ответ:10
- 45. Задача 28В классе учится 25 учащихся. Несколько
- 46. Решение задачи 2812 человек ходили в кино,
- 47. Задача 29На ленте по разные стороны от
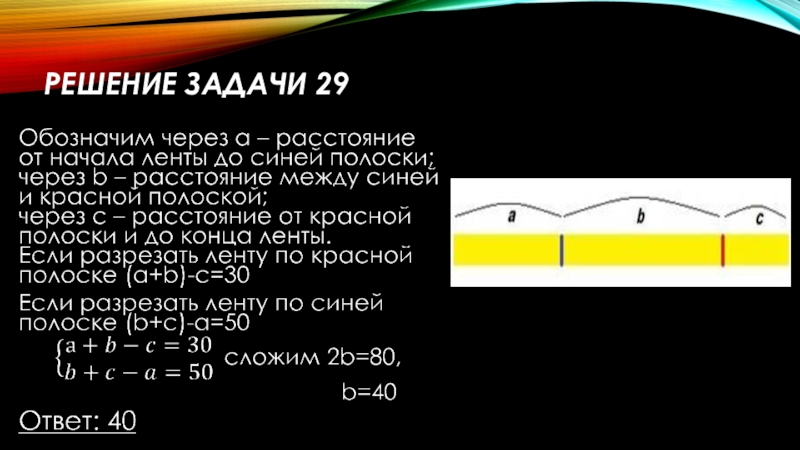
- 48. Решение задачи 29
- 49. Задача 30На ленте с разных сторон от
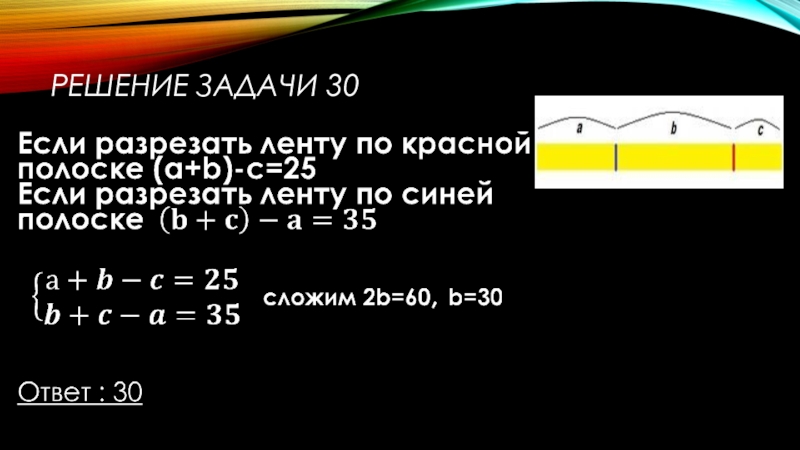
- 50. Решение задачи 30
- 51. Задача 31На ленте с разных сторон от
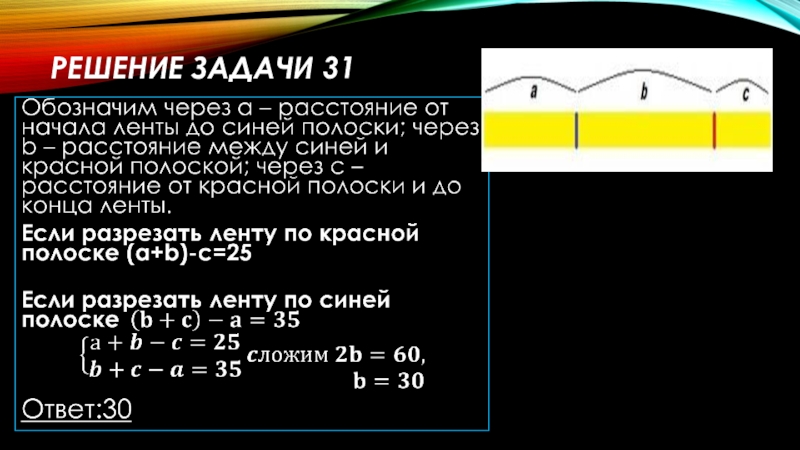
- 52. Решение задачи 31
- 53. Интернет источники Чертёжи к задачам 25-27
Слайд 1 Задания на смекалку
Слайд 2Задача 1
На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая,
Задача 2
На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. Сколько роз в белой вазе?
Слайд 3Решение задачи 1
Из первого условия следует, что в белой и оранжевой
Ответ: 3
Решение задачи 2
Из первого условия следует, что в синей и белой вазах 15 роз (в сумме).Тогда в красной вазе 22-15=7роз. Из второго условия задания следует, что в белой и красной вазах 12 роз. Поэтому в белой вазе 12-7= 5роз.
Ответ: 5
Слайд 4Задача 3
Маша и Медведь съели 160 печений и банку варенья, начав и
Задача 4
Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь - печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?
Слайд 5Решение задачи 3
Медведь съел свою половину банки варенья в 3 раза
Т.к. Медведь ест печенье в 3 раза быстрее, чем Маша и ещё у него осталось в 3 раза больше времени (он съел в 3 раза быстрее свою половину банки варенья), то он съедает в 3 ⋅ 3= 9 раз больше печений, чем Маша (9 печений съедает Медведь, в то время как Маша только 1 печенье).
Получается , что в отношении 9 : 1 едят Медведь и Маша печенье. Всего получается 10 долей, значит, 1 доля равна 160 : 10 =16. В итоге , Медведь съел 16⋅ 9 =144 печений.
Ответ: 144
Решение задачи 4
Медведь съел свою половину банки варенья в 3 раза быстрее, чем Маша, значит, у него ещё осталось в 3 раза больше времени на кушанье печенья.
Т.к. Медведь ест печенье в 3 раза быстрее, чем Маша и ещё у него осталось в 3 раза больше времени (он съел в 3 раза быстрее свою половину банки варенья), то он съедает в 3 ⋅ 3= 9 раз больше печений, чем Маша (9 печений съедает Медведь, в то время как Маша только 1 печенье).
Получается , что в отношении 9 : 1 едят Медведь и Маша печенье. Всего получается 10 долей, значит, 1 доля равна 100 : 10 =10. В итоге , Медведь съел 10⋅ 9 =90 печений.
Ответ: 90
Слайд 6Задача 5
Если бы каждый из двух сомножителей увеличили на 1, их
Задача 6
Если бы каждый из двух сомножителей увеличили на 1, их произведение увеличилось бы на 3. На самом деле каждый из двух сомножителей увеличили на 5. На сколько увеличилось произведение?
Слайд 7Решение задачи 5
Пусть первый сомножитель равен a, а второй b, их
ab +a + b +1 –ab = 11
a+ b = 10 Теперь вычислим, на сколько увеличится произведение, если сомножители увеличить на 2 : ( a+2)(b+2) – ab = ab +2a + 2b +4 –ab =
= 2( a + b) + 4 = 2⋅ 10 + 4= 24
Ответ: 24
Решение задачи 6
Пусть первый сомножитель равен a, а второй b, их произведение равно ab. При увеличении этих сомножителей на 1 их произведение возрастает на 11, то есть, (a+1)(b+1) – ab = 3
ab +a + b +1 –ab = 3
a+ b = 2 Теперь вычислим, на сколько увеличится произведение, если сомножители увеличить на 5 : ( a+5)(b+5) – ab = ab +5a + 5b +25 –ab = = 5( a + b) + 25 = 5⋅ 2 + 25= 35
Ответ: 35
Слайд 8Задача 7
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц
Задача 8
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Слайд 9Решение задачи 7
Х – вероятность того, что яйцо купленное у этой
1 - х -– вероятность того, что яйцо купленное у этой агрофирмы окажется из второго хозяйства
0,4х +0,2 (1- х) = 0,35
0,4х + 0,2 - 0,2х = 0,35
0,2х = 0,15
Х = 0,75
Ответ : 0,75
Решение задачи 8
Х – вероятность того, что яйцо купленное у этой агрофирмы окажется из первого хозяйства,
1 - х -– вероятность того, что яйцо купленное у этой агрофирмы окажется из второго хозяйства
0,6х +0,7 (1- х) = 0,65
0,6х + 0,7 - 0,7х = 0,65
-0,1х = -0,05
Х = 0,5
Ответ : 0,5
Слайд 10Задача 9
Из десяти стран семь подписали договор о дружбе ровно с
Слайд 11Решение задачи 9
Две страны подписывают один общий договор. На каждом договоре
Найдем число подписей: 7⋅3+3⋅7= 42
Найдем число подписанных договоров: 42:2=21
Ответ: 21
Слайд 12Задача 10
Хозяин договорился с рабочими, что они копают колодец на следующих
Слайд 14Задача 11
Хозяин договорился с рабочими, что они выкопают ему колодец на
Слайд 16Задача 12
По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый
Слайд 18Задача 13
Тренер посоветовал Андрею в первый день занятий провести на беговой
Слайд 20Задача 14
В результате паводка котлован заполнился водой до уровня 2 метра.
Слайд 21Решение задачи 14
2м=2× 100 = 200 см – уровень воды перед
Слайд 22Задача 15
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по
Слайд 23Решение задачи 15
Учитывая заливание скважины, в течении суток
проходят 300 - 30=270
пройдено ещё 300 метров.
Ответ :11
Слайд 24Задача 16
Ящики двух видов, имеющие одинаковую ширину и высоту, укладывают на
Слайд 25Решение задачи 16
Так как надо найти наименьшее число ящиков, то надо
Слайд 26Задача 17
В таблице три столбца и несколько строк. В каждую клетку
Слайд 27Решение задачи 17
119 + 125 + 133 = 377- сумма чисел
Числа 18 и 15 не включены в предел, значит:
1) если сумма в строке равна17, то, количество строк равно 377 : 17= =22,2
2) если сумма в строке равна 16, то, количество строк равно 377 : 16= =23,5. Т.к. число строк целое число и лежит в пределах 22,2<Х< 23,5 .Значит количество строк равно 23.
Ответ: 23
Слайд 28Задача 18
Список заданий викторины состоял из 36 вопросов. За каждый правильный
Слайд 29Решение задачи 18
1 способ: Балл за каждый верный ответ –
2 способ: Пусть Х – количество верных ответов
у – количество неверных ответов.
Тогда составим уравнение 5х -11у = 75, -11у=75-5х, -11у = 5(15-х) ,где 0<х<36 и 0<у<36. Из уравнения видно, что у делится на 5.
Пусть: 1) у=5, тогда 5х = 75 + 11у= 75 + 55=130, тогда х = 130 : 5 = 26 и это меньше 36. 2) у=10, тогда 5х =75 +11у=75+110=185, тогда х= 185 : 5=37, но это больше 36.
Ответ:26
Слайд 30Задача 19
Список заданий викторины состоял из 25 вопросов. За каждый правильный
25-10+1=16
Задача 20
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 9 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 56 очков, если известно, что по крайней мере один раз он ошибся?
25-9+1=17
Слайд 31Задача 21
Врач прописал пациенту принимать лекарство по такой схеме: в первый
Слайд 33Задача 22
Врач прописал пациенту принимать лекарство по такой схеме: в первый
Слайд 35Задача 23
В меню ресторана имеется 6 видов салатов, 3 вида первых
Слайд 36Решение задачи 23
Салат можно выбрать 6 способами, первое –
6⋅3⋅5⋅4 =360
Ответ : 360
Слайд 37Задача 24
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели
Слайд 38Решение задачи 24
50+65+80+95+10+60+50+40+30+20+10=290+220=510 мин, 510:60=8,5 час
Ответ: 8,5
Слайд 39Задача 25
На кольцевой дороге расположены четыре бензоколонки: A, B, C и
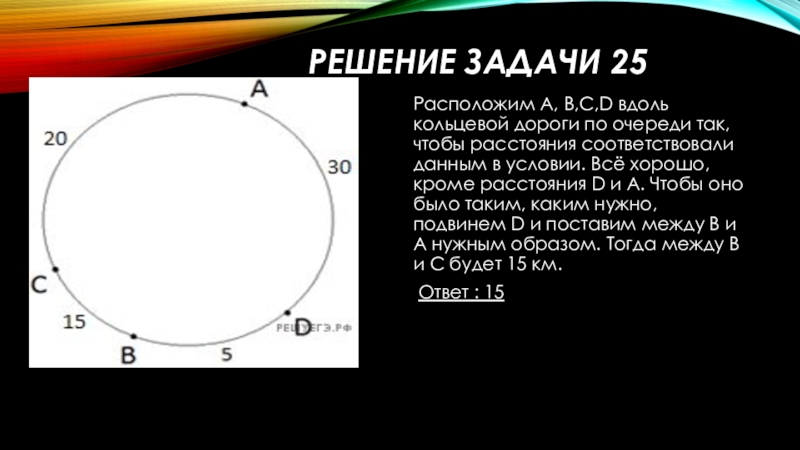
Слайд 40Решение задачи 25
Расположим А, В,С,D вдоль кольцевой дороги по очереди так,
Ответ : 15
Слайд 41Задача 26
На кольцевой дороге расположены четыре бензоколонки: A, B, C и
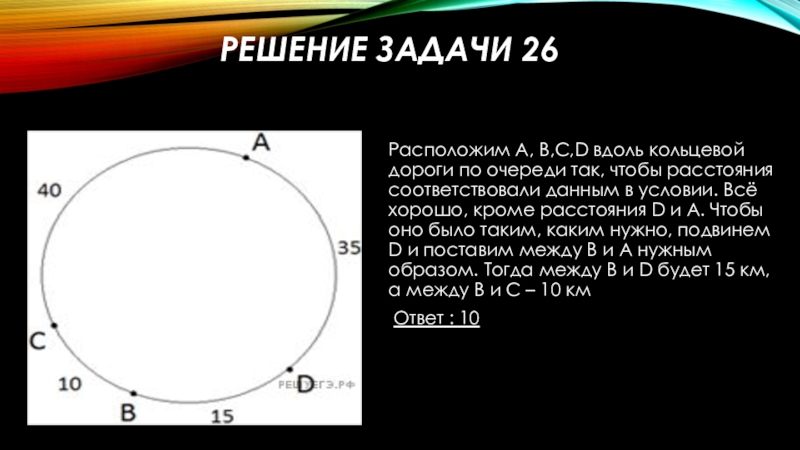
Слайд 42Решение задачи 26
Расположим А, В,С,D вдоль кольцевой дороги по очереди так,
Ответ : 10
Слайд 43Задача 27
На кольцевой дороге расположены четыре бензоколонки: A, Б, B, и
Слайд 45Задача 28
В классе учится 25 учащихся. Несколько из них ходили в
Слайд 46Решение задачи 28
12 человек ходили в кино, и в театр. А
Сходили в театр или в кино и в театр, или никуда не ходили 12+6+3= 21человек. Значит, 25 – 21 =4 человека ходили только в кино. И значит всего в кино сходило 14+12=16
Ответ:16
Слайд 47Задача 29
На ленте по разные стороны от середины отмечены две тонкие
Слайд 49Задача 30
На ленте с разных сторон от середины отмечены две поперечные
Слайд 51Задача 31
На ленте с разных сторон от середины отмечены две поперечные
Слайд 53 Интернет источники
Чертёжи к задачам 25-27 на сайте
Чертёжи к задачам 29-31 на сайте selt- edu.ru › ege 2019– base_30.php?id =15__20.
3.Открытый банк заданий ЕГЭ на сайте ФИПИ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege
4. Решу ЕГЭ, образовательный портал для подготовки к экзаменам http://mathb.reshuege.ru/
5.Открытый банк заданий по математике http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege