- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теория вероятностей в курсе алгебры 9 класса
Содержание
- 1. Презентация по математике Теория вероятностей в курсе алгебры 9 класса
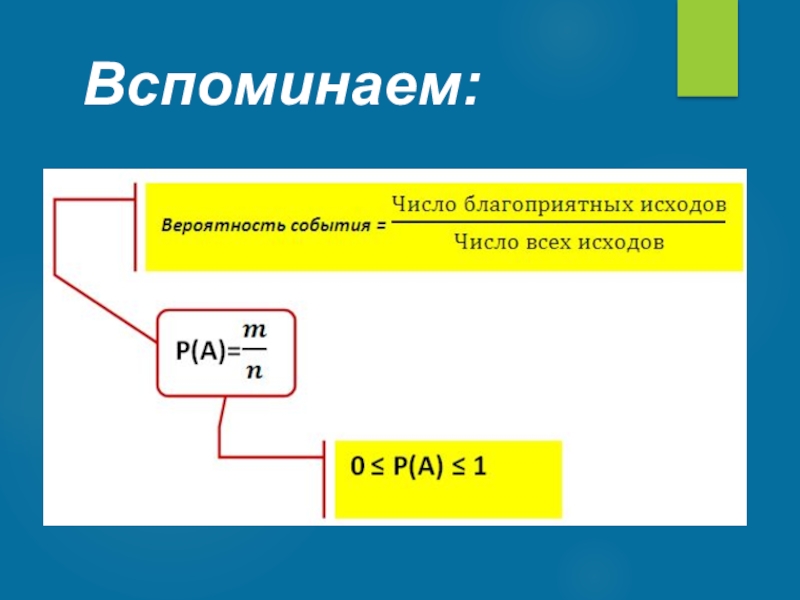
- 2. Вспоминаем:
- 3. БРОСАНИЕ МОНЕТЫ
- 4. 1. Монета брошена два раза. Какова
- 5. 2. Монета брошена три раза. Какова
- 6. 3. В случайном эксперименте симметричную монету бросают
- 7. ИГРА В КОСТИ
- 8. 4. Определите вероятность того, что при
- 9. 5. Брошена игральная кость. Найдите вероятность
- 10. 6. В случайном эксперименте бросают две игральные кости.
- 11. 7. Дважды бросают игральный кубик. В
- 12. ЛОТЕРЕЯ
- 13. 8. На экзамене 50 билетов, Тимофей
- 14. СОРЕВНОВАНИЯ
- 15. 9. В чемпионате по гимнастике участвуют 20
- 16. 10. На соревнования по метанию ядра приехали
- 17. 11. Перед началом первого тура чемпионата по
- 18. 12. Конкурс исполнителей проводится в 5 дней.
- 19. ЧИСЛА
- 20. 13. Максим выбирает двузначное число. Найдите вероятность
- 21. РАЗНЫЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- 22. 14. Фабрика выпускает сумки. В среднем на
- 23. 15. В среднем из каждых 100 поступивших
- 24. РефлексияСегодня на уроке я запомнил……..Я научился…………………….Я понял……………………………У меня не получилось………………….Мне хотелось бы………………………
Слайд 41. Монета брошена два раза. Какова вероятность выпадения одного «орла» и
Решение:
При бросании одной монеты возможны два исхода –
«орёл» или «решка».
При бросании двух монет: 4 исхода (2 . 2=4):
«орёл» - «решка» ОР
«решка» - «решка» РР
«решка» - «орёл» РО
«орёл» - «орёл» ОО
Один «орёл» и одна «решка» выпадут в двух случаях из четырёх.
Р(А)= =0,5.
Ответ: 0,5.
Слайд 52. Монета брошена три раза. Какова вероятность выпадения двух «орлов» и
Решение:
При бросании трёх монет возможны 8 исходов (2*2*2=8):
«орёл» - «решка» - «решка» ОРР
«решка» - «решка» - «решка» РРР
«решка» - «орёл» - «решка» РОР
«орёл» - «орёл» - «решка» ООР
«решка» - «решка» -«орёл» РРО
«решка» - «орёл» - «орёл» РОО
«орёл» - «решка» - «орёл» ОРО
«орёл» - «орёл» - «орёл» ООО
Два «орла» и одна «решка» выпадут в трёх случаях из восьми.
Р(А)=3/8=0,375.
Ответ: 0,375.
Слайд 63. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того,
Решение:
При бросании четырёх монет возможны 16 исходов: (2*2*2*2=16):
Благоприятных исходов – 1 (выпадут четыре решки).
Р(А)=1/16=0,0625.
Ответ: 0,0625.
Математическая монета считается симметричной. Это означает, что брошенная на стол монета имеет равные шансы выпасть «орлом» или «решкой». При этом подразумевается, что никакой другой исход бросания монеты невозможен, — она не может потеряться, закатившись в угол, и, тем более, не может «встать на ребро».
Слайд 84. Определите вероятность того, что при бросании кубика выпало больше трёх
Решение:
Всего возможных исходов : 6.
Числа большие 3 : это 4, 5, 6 - их 3.
Р(А)= 3/6=0,5.
Ответ: 0,5.
Слайд 95. Брошена игральная кость. Найдите вероятность того, что выпадет чётное число
Решение:
Всего возможных исходов: 6
1, 3, 5 — нечётные числа;
2, 4, 6 —чётные числа.
Вероятность выпадения чётного числа очков равна Р(А)= 3/6=0,5.
Ответ: 0,5.
Слайд 106. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме
Решение:
У данного действия — бросания двух игральных костей
всего 36 возможных исходов, так как 6² = 36.
Благоприятные исходы:
2 6 т.к 2+6=8
3 5 т.к.3+5=8
4 4
5 3
6 2
Вероятность выпадения восьми очков равна
Р(А)= 5/36 ≈ 0,13 (8) ≈ 0,14.
Ответ: 0,14.
Слайд 117. Дважды бросают игральный кубик. В сумме выпало 6 очков. Найдите
Решение: Всего исходов выпадения 6 очков: 5.
2 и 4; т.к.2+4=6
4 и 2; т.к.4+2=6
3 и 3;
1 и 5;
5 и 1.
Благоприятных исходов - 2.
Р(А)=2/5=0,4.
Ответ: 0,4.
Слайд 138. На экзамене 50 билетов, Тимофей не выучил 5 из них.
Решение:
Тимофей выучил 50-5= 45 билетов.
Р(А)=45/50=0,9.
Ответ: 0,9.
Слайд 159. В чемпионате по гимнастике участвуют 20 спортсменов: 8 из России,
Решение:
Всего исходов: 20.
Благоприятных исходов 20-(8+7)=5.
Р(А)=5/ 20=0,25.
Ответ: 0,25.
Слайд 1610. На соревнования по метанию ядра приехали 4 спортсмена из Франции,
Решение:
Число всех возможных исходов: 4 + 5 + 3 = 12
Число благоприятных исходов: 3.
Р(А)=3/12=0,25.
Ответ: 0,25.
Слайд 1711. Перед началом первого тура чемпионата по бадминтону участников разбивают на
Решение:
Всего исходов: 25 (Олег Буров и 25 бадминтонистов).
Благоприятных исходов: (12-1)=11.
Р(А)=11/25 = 0,44.
Ответ: 0,44.
Слайд 1812. Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по
Решение:
Всего исходов : 75.
Исполнители из России выступают на третий день.
Благоприятных исходов – (75-27):4=48: 4 =12.
Р(А)=12 / 75 = 0,16.
Ответ: 0,16 .
Слайд 2013. Максим выбирает двузначное число. Найдите вероятность того, что оно делится
Решение:
Двузначные числа: 10; 11; 12; … ; 99.
Всего исходов : 99- 9 = 90
Числа, делящиеся на 5:
10; 15; 20; 25; …; 90; 95.
Благоприятных исходов: 95 : 5 – 1 = 19 – 1 = 18.
Р(А)=18 / 90 = 0,2.
Ответ: 0,2.
Слайд 2214. Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится
Решение:
Всего исходов: 170 + 6 = 176.
Благоприятных исходов: 170.
Р(А)=170 / 176 ≈ 0,9659… ≈ 0,97.
Ответ: 0,97.
Слайд 2315. В среднем из каждых 100 поступивших в продажу аккумуляторов 94
Решение:
Всего исходов : 100.
Благоприятных исходов: 100 – 94 = 6.
Р(А)=6 /100=0,06.
Ответ: 0,06.