- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Решение комбинаторных задач Подготовка к ЕГЭ
Содержание
- 1. Презентация по математике Решение комбинаторных задач Подготовка к ЕГЭ
- 2. Слайд 2
- 3. Правило суммыЕсли элемент x можно выбрать способами
- 4. Пример 1В коробке 10 тетрадей в клетку
- 5. Пример1. Сколько существует способов выбрать кратное двум
- 6. Правило произведенияЕсли элемент x можно выбрать nx
- 7. Пример 2В магазине "Все для чая'' есть
- 8. Пример 2. а) Сколько различных двузначных чисел
- 9. Пример5. Несколько стран в качестве символа своего
- 10. б) Сколько стран могут использовать такую символику
- 11. Пример7. Сколькими способами можно посадить шестерых школьников
- 12. Пусть Коля сидит на краю. Место на
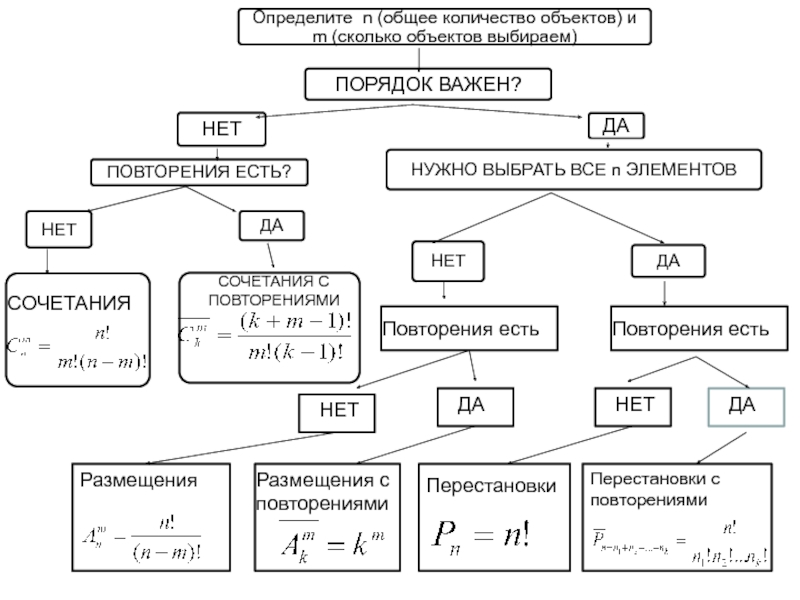
- 13. Повторения естьПовторения естьНЕТДАРазмещенияРазмещения с повторениямиПерестановкиПерестановки с повторениямиДА
- 14. Перестановки
- 15. Перестановки без повторенийПерестановками без повторений из n
- 16. Перестановки без повторений6 различных перестановок
- 17. Сколькими способами 4 человека могут разместиться в четырехместном купе?
- 18. Задача 19. Даны цифр: 1,2,3,4,5,6,7. Сколько различных
- 19. Перестановки с повторениямиПерестановки с повторением из n
- 20. Перестановки с повторениямиn1=2n2=1n=n1+n2=2+1=33 различные перестановки
- 21. Пример 4Дворовая футбольная команда выбирает капитана и
- 22. Пример 5Сколько различных гирлянд можно сделать, если
- 23. Пример Даны цифр: 1,2,2,3,3,3,4,. Сколько различных чисел
- 24. Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
- 25. Сколько различных гирлянд получится, если замкнуть гирлянду из предыдущей задачи в кольцо?
- 26. Размещения(выборки)
- 27. Размещения без повторенийРазмещениями без повторений из n
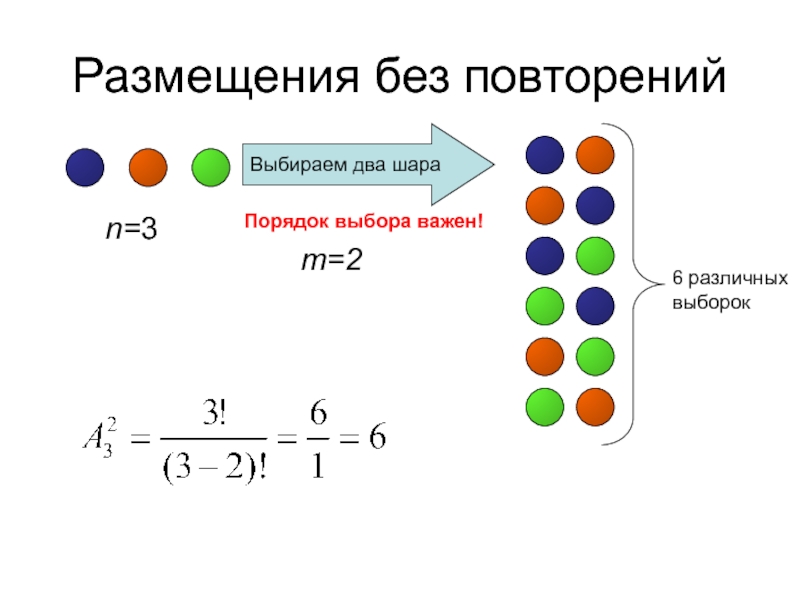
- 28. Размещения без повторенийn=3Выбираем два шараm=2Порядок выбора важен!6 различных выборок
- 29. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
- 30. Пример Из группы в 15 человек выбирается
- 31. Размещения с повторениямиРазмещения с повторениями из элементов
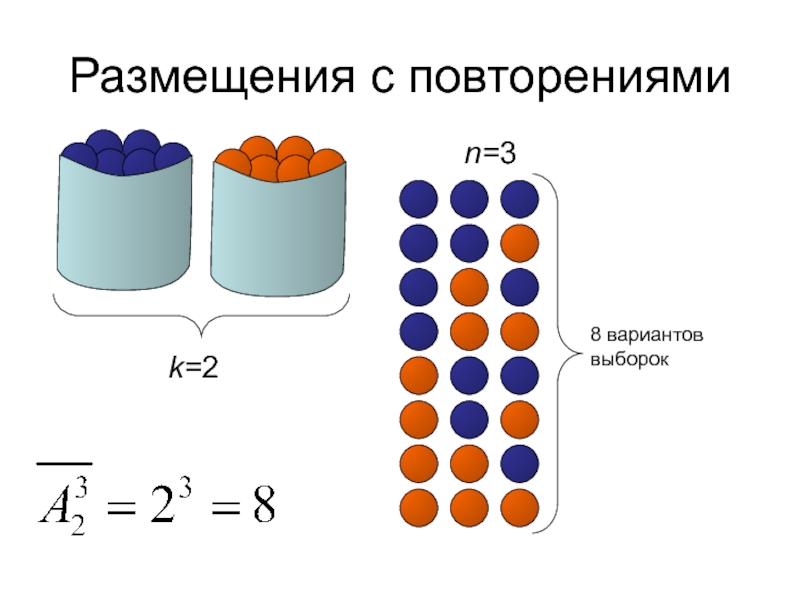
- 32. Размещения с повторениямиk=2n=38 вариантов выборок
- 33. Пример 8Назовем натуральное число "симпатичным", если в
- 34. Шифр сейфа состоит из 6 цифр, которые
- 35. Сочетания
- 36. Сочетания без повторенийСочетаниями без повторений из n
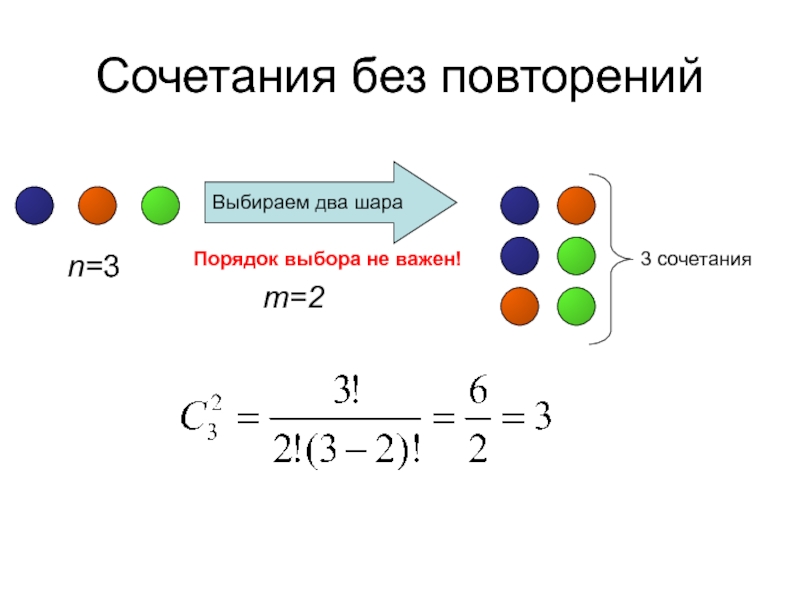
- 37. Сочетания без повторенийn=3Выбираем два шараm=2Порядок выбора не важен!3 сочетания
- 38. Пример 9Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
- 39. Сколькими способами можно вывезти со склада 10
- 40. Сочетания с повторениямиСочетаниями с повторениями из элементов
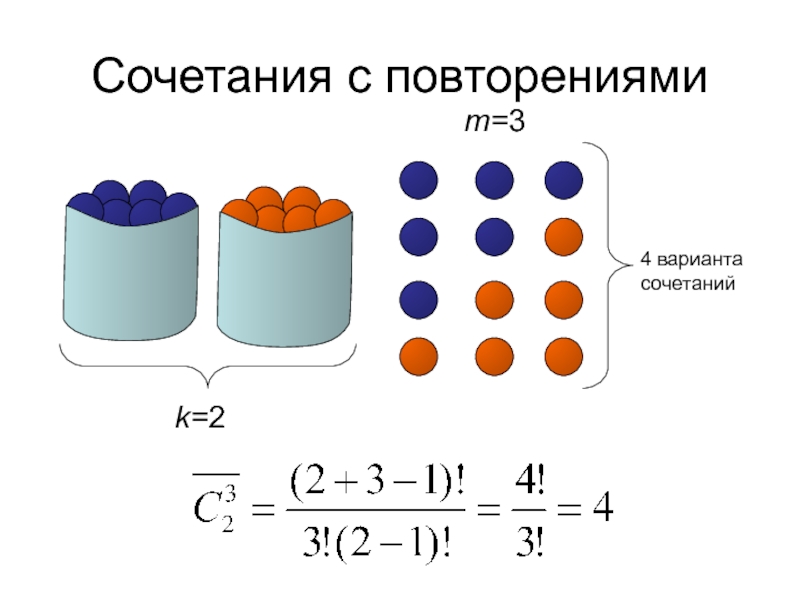
- 41. Сочетания с повторениямиk=2m=34 варианта сочетаний
- 42. Пример 10В вазе стоят 10 красных и
- 43. В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?
- 44. Слайд 44
- 45. Один выбор (анализ) элементов или несколько? Если
- 46. Сколько различных гирлянд можно сделать из 10
- 47. Пример 11Световое табло состоит из лампочек. Каждая
- 48. У людоеда в подвале томятся 25 пленников.
- 49. Волонтеры разделились на две равные группы для
- 50. Сколько существует натуральных чисел, меньших 25610, таких,
- 51. 3) Рассмотрим шестиразрядные числа. Рассуждая аналогично п.1
- 52. Пример 15В коробке находятся 16 шариков –
- 53. Сколькими способами можно расставить белые фигуры (короля,
- 54. Из цифр 1, 2, 3, 4, 5,
- 55. В стране 20 городов, каждые два из
Правило суммыЕсли элемент x можно выбрать способами nx и если элемент y можно выбрать ny способами, то выбор «либо x, либо y» можно осуществить способами nx+ ny.Nx=4Ny=5Выбираем один шарЛюбой цветNx +Ny=4+5=9 способов
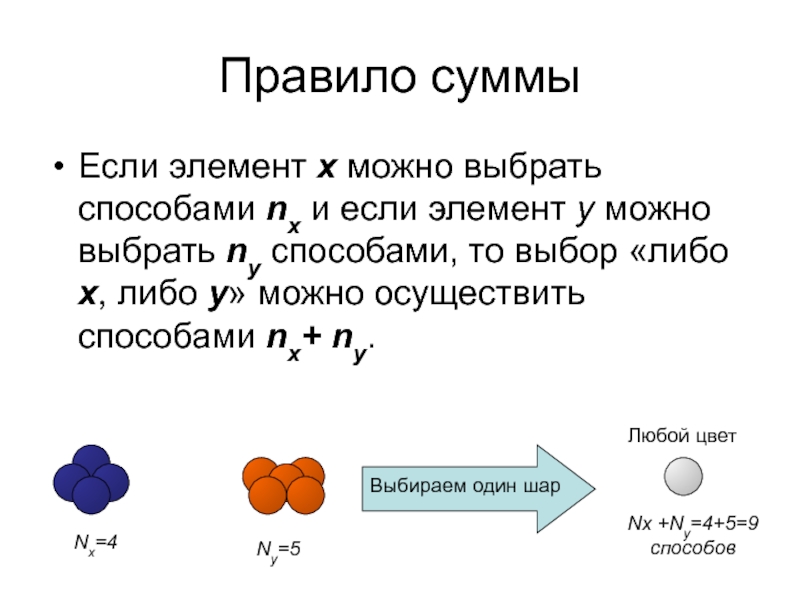
Слайд 3Правило суммы
Если элемент x можно выбрать способами nx и если элемент
y можно выбрать ny способами, то выбор «либо x, либо y» можно осуществить способами nx+ ny.
Nx=4
Ny=5
Выбираем один шар
Любой цвет
Nx +Ny=4+5=9 способов
Слайд 4Пример 1
В коробке 10 тетрадей в клетку и 5 тетрадей в
линию. Сколькими способами можно выбрать одну тетрадь?
Решение: или – логическая сумма
10+5=15 (выбор неважен)
Решение: или – логическая сумма
10+5=15 (выбор неважен)
Слайд 5Пример1. Сколько существует способов выбрать кратное двум или трем число из
множества чисел : 2,3,4,15,16,20,21, 75,28 ?
Решение:
к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
к1+к2 = 5+4 = 9
Решение:
к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
к1+к2 = 5+4 = 9
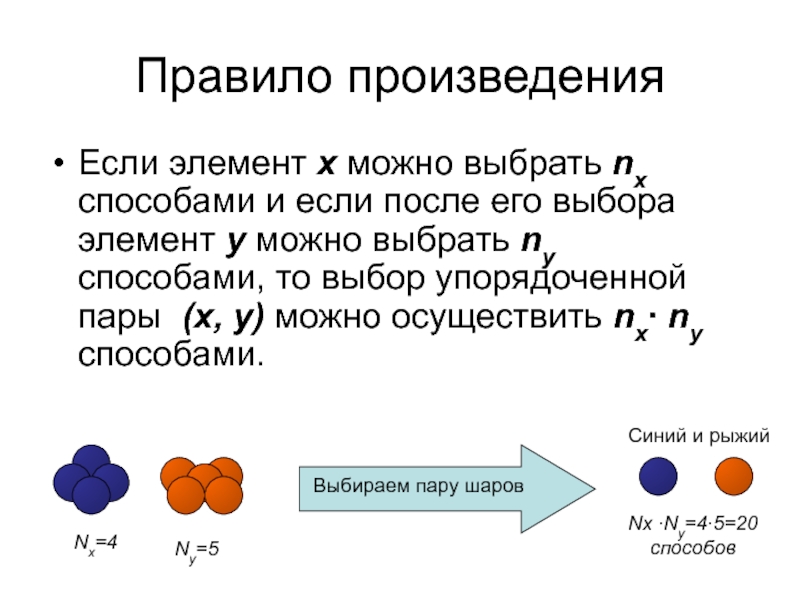
Слайд 6Правило произведения
Если элемент x можно выбрать nx способами и если после
его выбора элемент y можно выбрать ny способами, то выбор упорядоченной пары (x, y) можно осуществить nx∙ ny способами.
Nx=4
Ny=5
Выбираем пару шаров
Синий и рыжий
Nx ∙Ny=4∙5=20 способов
Слайд 7Пример 2
В магазине "Все для чая'' есть 5 разных чашек и
3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
5*3=15
5*3=15
Слайд 8Пример 2. а) Сколько различных двузначных чисел можно составить из цифр
1,3,5,7,9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5х1 =5
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5х1 =5
Слайд 9Пример5. Несколько стран в качестве символа своего государства решили использовать флаг
в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
а)Сколько всего стран могут использовать такую символику?
Решение: Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N=4х3х2х1=24
а)Сколько всего стран могут использовать такую символику?
Решение: Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N=4х3х2х1=24
Слайд 10б) Сколько стран могут использовать такую символику с синей и красной
полосами, расположенными рядом?
Решение: Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
Решение: Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
Слайд 11Пример7. Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы
Коля и Оля оказались рядом?
Решение: Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
Решение: Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
Слайд 12Пусть Коля сидит на краю. Место на краю можно выбрать 2
способами, после чего Олю можно посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
4х2х4х3х2х1=192 способами.
По правилу сложения 48+192= 240 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
4х2х4х3х2х1=192 способами.
По правилу сложения 48+192= 240 способов
Слайд 13Повторения есть
Повторения есть
НЕТ
ДА
Размещения
Размещения с повторениями
Перестановки
Перестановки с повторениями
ДА
Слайд 15Перестановки без повторений
Перестановками без повторений из n различных элементов называются все
возможные последовательности этих n элементов. Число перестановок без повторений из n элементов равняется
по определению
по определению
Слайд 18Задача 19. Даны цифр: 1,2,3,4,5,6,7. Сколько различных чисел можно составить из
этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1234567, 2354167, 7546321.
Перестановка-упорядоченное множество.
Число перестановок из n элементов вычисляют по формуле Pn=n!.
По условию n=7
Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.
Примеры: 1234567, 2354167, 7546321.
Перестановка-упорядоченное множество.
Число перестановок из n элементов вычисляют по формуле Pn=n!.
По условию n=7
Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.
Слайд 19Перестановки с повторениями
Перестановки с повторением из n элементов k типов
число
элементов 1-го типа n1;
число элементов 2-го типа n2; …;
число элементов k-го типа nk,
все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают
подсчитывают так:
все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают
подсчитывают так:
Слайд 21Пример 4
Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами
это можно сделать, если в команде 11 человек?
Слайд 22Пример 5
Сколько различных гирлянд можно сделать, если у нас 5 красных,
7 синих и 4 желтых светодиода?
Слайд 23Пример Даны цифр: 1,2,2,3,3,3,4,. Сколько различных чисел можно составить из этих
цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1223334, 4232331,2233314.
Некоторые числа при перестановке одинаковых цифр не меняются.
По условию n=7, n1=2 , n2=3
Примеры: 1223334, 4232331,2233314.
Некоторые числа при перестановке одинаковых цифр не меняются.
По условию n=7, n1=2 , n2=3
Слайд 24Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную
и четырехместную?
Слайд 27Размещения без повторений
Размещениями без повторений из n различных элементов по m
элементов называются все такие последовательности m различных элементов, выбранных из исходных n, которые отличаются друг от друга или порядком следования элементов, или составом элементов.
Число размещений без повторений из n элементов по m обозначается символом
Число размещений без повторений из n элементов по m обозначается символом
Слайд 29Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания
при выборе из 11 дисциплин.
Слайд 30Пример
Из группы в 15 человек выбирается 4 участника эстафеты 800+400+200+100.
Сколькими способами можно расставить спортсменов по этапам эстафеты?
Слайд 31Размещения с повторениями
Размещения с повторениями из элементов k типов по m
элементов (k и m могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличаются друг от друга или порядком следования элементов, или составом элементов.
Слайд 33Пример 8
Назовем натуральное число "симпатичным", если в его записи встречаются только
нечетные цифры. Сколько существует четырехзначных "симпатичных" чисел?
k=5 порядок важен
k=5 порядок важен
Слайд 34Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и
могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Слайд 36Сочетания без повторений
Сочетаниями без повторений из n различных элементов по m
элементов называются все такие последовательности m различных элементов, выбранных из исходных n, которые отличаются друг от друга составом элементов.
Слайд 39Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах,
если на каждую автомашину грузят по 5 ящиков.
Слайд 40Сочетания с повторениями
Сочетаниями с повторениями из элементов k типов по m
элементов (m и k могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличают друг от друга составом элементов.
Слайд 42Пример 10
В вазе стоят 10 красных и 4 розовых гвоздики. Все
цветы на внешний вид одинаковы. Сколькими способами можно выбрать 3 цветка из вазы?
Решение
Так как по условию задачи все цветы на внешний вид одинаковы, то мы получаем формулу без повторений.
Вы выбираем цветы в букет, порядок выбора не важен, следовательно, мы получаем формулу сочетаний без повторений: два типа цветов, выбираем три цветка.
Слайд 43В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить
12 открыток для поздравлений?
Слайд 45Один выбор (анализ) элементов или несколько? Если один, то см. п.3
Каким
союзом варианты выбора (анализа) соединяются? «И» – правило произведения, «или» – правило суммы.
Для каждого выбора задаются следующие вопросы:
Все элементы используются? Если «да», то это перестановки. Переходим к п. 5.
Порядок выбора элементов важен? Если «да», то это размещения, «нет» – сочетания.
Есть ли одинаковые элементы? Если «да» – то формула с повторениями, «нет» – без повторений.
Для каждого выбора задаются следующие вопросы:
Все элементы используются? Если «да», то это перестановки. Переходим к п. 5.
Порядок выбора элементов важен? Если «да», то это размещения, «нет» – сочетания.
Есть ли одинаковые элементы? Если «да» – то формула с повторениями, «нет» – без повторений.
Слайд 46Сколько различных гирлянд можно сделать из 10 светодиодов разного цвета?
При замыкании
линии в кольцо перестановки, являющиеся циклическими сдвигами относительно друг друга, становятся одинаковыми.
Возьмем, например, следующую перестановку и посмотрим, сколько других перестановок явлюяются ее циклическим сдвигом:
1. ккккксссссссжжжж
2. кккксссссссжжжжк
3. ккксссссссжжжжкк
...
15. жжккккксссссссжж
16. жккккксссссссжжж
Следовательно, все перестановки разбиваются на группы по 16 цепочек в группе. Итак, число кольцевых гирлянд будет
Слайд 47Пример 11
Световое табло состоит из лампочек. Каждая лампочка может находиться в
одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?
Слайд 48У людоеда в подвале томятся 25 пленников.
а) Сколькими способами он
может выбрать трех из них себе на завтрак, обед и ужин?
б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?
б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?
Решение 25*24*23 = 13800 способов.
Заметим, что в предыдущем пункте каждую тройку пленников мы посчитали 3·2·1 = 6 раз. Поскольку теперь их порядок нам неважен, то ответом будет число 13800 : 6 = 2300.
Слайд 49Волонтеры разделились на две равные группы для розыска заблудившегося ребенка. Среди
них только 4 знакомы с местностью. Каким числом способов они могут разделиться так, чтобы в каждую группу вошло 2 человека, знающих местность, если всего их 16 человек?
Решение
Мы делим всех волонтеров на две равные группы, то есть выбираем участников первой группы, а все остальные переходят в другую группу. Один выбор.
Теперь рассмотрим этот выбор первой группы. Выбор состоит из выбора волонтеров, знающих местность, и выбора волонтеров, незнающих местность. Следовательно, будем соединять эти два числа правилом произведения.
Найдем число выборов волонтеров, знающих местность. Всего таких волонтеров 4 человека. Нам нужно 2. Порядок выбора не важен. Сочетания без повторений.
Найдем число выборов волонтеров, незнающих местность. Всего их 16-4=12 , выбираем шесть человек (ровно половину).
Общее число выборов:
Слайд 50Сколько существует натуральных чисел, меньших 25610, таких, что в записи каждого
числа в двоичной системе счисления будет равное количество единиц и значащих нулей. В ответе укажите целое число.
Решение
Переведем данное число из десятичной системы счисления в двоичную.
25610 =1000000002
Следовательно, числа меньше данного состоят из восьми, семи, шести, пяти, четырех, трех, двух и одного разряда.
1) Рассмотрим восьмиразрядные числа. 1ХХХХХХХ. Так как мы точно знаем сколько нулей и единиц, то мы используем формулу перестановки с повторениями.
2) Рассмотрим семиразрядные числа. Очевидно, что такие числа не удовлетворяют условию задачи, так как не могут состоять из одинакового числа единиц и нулей. Аналогичный вывод можно сделать о пятиразрядных, трехразрядных и одноразрядных числах.
Слайд 513) Рассмотрим шестиразрядные числа. Рассуждая аналогично п.1 получаем:
4) Четырехразрядные числа.
5) Двухразрядное
число только одно 102
Итак, у нас может быть или восьмиразрядное число, или шестиразрядное число, или четырехразрядное число, или двухразрядное число. Правило суммы.
Слайд 52Пример 15
В коробке находятся 16 шариков – 4 красных, 4 синих
и 8 черных. Из коробки наугад вынули два шарика. Какое из перечисленных сообщений несет в себе наибольший объем информации?
Один из вынутых шариков – красного цвета, а другой – синего;
Один из вынутых шариков – синего цвета, а другой – черного;
Оба вынутых шарика красного цвета;
Оба вынутых шарика черного цвета;
Цвета вынутых шариков отличаются друг от друга;
Вынуты шарики одного и того же цвета.
Один из вынутых шариков – красного цвета, а другой – синего;
Один из вынутых шариков – синего цвета, а другой – черного;
Оба вынутых шарика красного цвета;
Оба вынутых шарика черного цвета;
Цвета вынутых шариков отличаются друг от друга;
Вынуты шарики одного и того же цвета.
Слайд 53Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2
слонов и 2 коней) на первой линии шахматной доски?
Слайд 54Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9
составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
Решение
В этой задаче нам обязательно нужно использовать цифры 2, 4 и 5. Но они могут стоять на разных местах и в разном порядке. У нас три "важные" и две "неважные" цифры в числе - два типа цифр. Это перестановки с повторениями.
Теперь посчитаем сколько различных перестановок "важных" цифр между собой. Это перестановки без повторений
Итак у нас 60 различных перестановок. Теперь посчитаем, сколько различных "неважных" цифр может быть в каждой из этих перестановок.
Мы выбираем две "неважные" цифры из шести. Порядок выбора важен. Это размещения без повторений.
Слайд 55В стране 20 городов, каждые два из которых соединены авиалинией. Сколько
авиалиний в этой стране?
Решение:
Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380.
Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
