- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему теория вероятности
Содержание
- 1. Презентация по математике на тему теория вероятности
- 2. Теория и практика Люди играют с
- 3. Теория и практика Если подброшенная на
- 4. Математические моделиматематическая модель "монета":
- 5. Количество выпадений "орла" при многократном подбрасывания монеты10
- 6. Математические моделиматематическая модель «игральная кость»:
- 7. События и испытанияПредметом исследования в теории вероятностей
- 8. Примеры испытаний и событийИспытание – бросание игральной
- 9. Вероятность случайного события Степень объективной возможности
- 10. События могут бытьДостоверныеНевозможныеСлучайныеНесовместныеНезависимыеПротивоположные
- 11. Достоверные события Событие называется достоверным,
- 12. Примеры достоверных событийНа игральном кубике выпадет меньше
- 13. Невозможные события Событие называют невозможным, если
- 14. Примеры невозможных событийПадение монеты на реброВыпадение на
- 15. Случайные события Событие называется случайным, если
- 16. Примеры случайных событийВыпадение на игральном кубике четного
- 17. Несовместные события События A и B
- 18. Примеры несовместных и совместимых событийсовместные события: идет
- 19. Независимые события События A и B
- 20. Примеры независимых событийНа обоих кубах выпадет шестерка;При
- 21. Противоположные события С каждым событием A
- 22. Примеры противоположных событийНа кубике выпадет четное число
- 23. Петя задумал натуральное число. Событие состоит в
- 24. Охарактеризуйте следующее событие:
- 25. ИСХОД ИСХОДОМ (или элементарным исходом,
- 26. Число возможных исходов в каждом из рассмотренных
- 27. а) В урне четыре шара с номерами
- 28. а) За городом N железнодорожные станции расположены
- 29. Действия над событиями 1. Суммой нескольких
- 30. Действия над событиями Пример. В урне
- 31. Примеры суммы событий:пусть А - идет дождь,
- 32. Действия над событиями 2. Произведением нескольких
- 33. Примеры произведения событий:пусть А - из урны
- 34. Задание 3 Опишите, в чем состоит
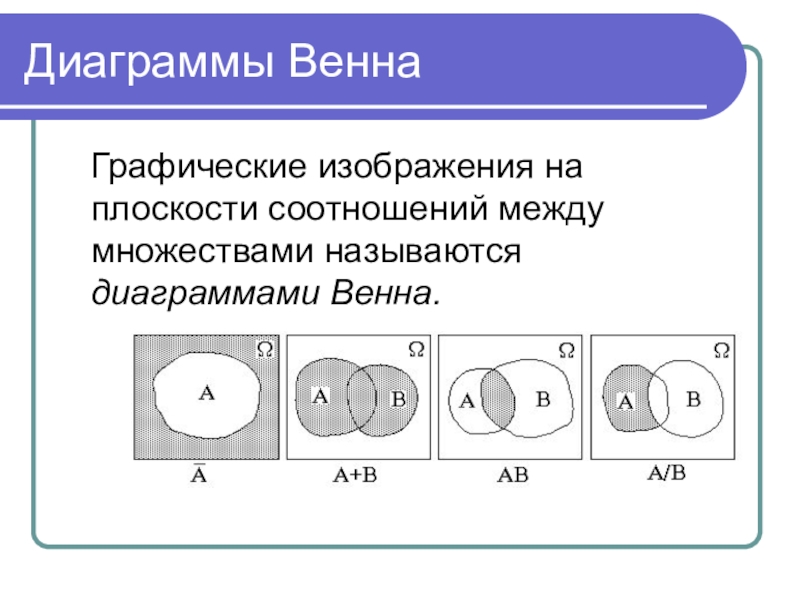
- 35. Диаграммы Венна Графические изображения на плоскости соотношений между множествами называются диаграммами Венна.
- 36. Дополнительные задания Задание 4.
- 37. ВопросыМогут ли события быть одновременно и несовместными
- 38. Вероятностью Р наступления случайного события
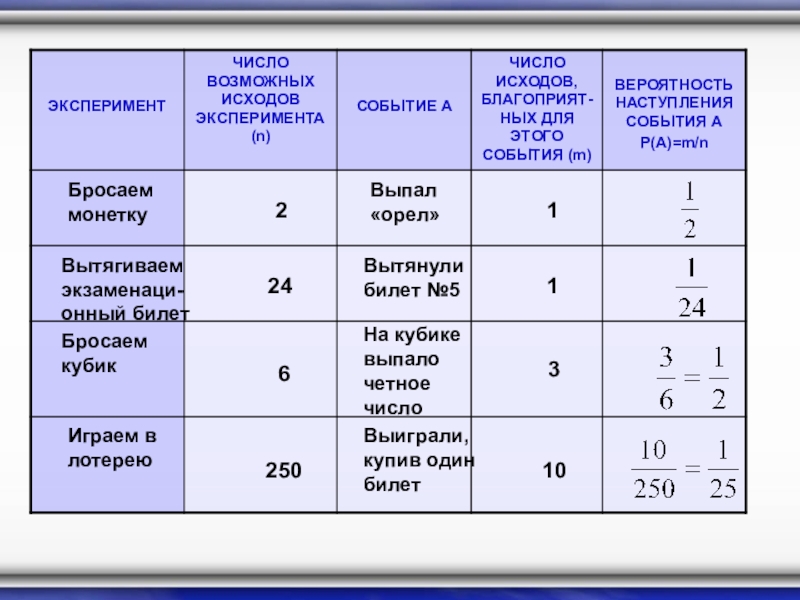
- 39. Бросаем монетку2Выпал «орел»1Вытягиваем экзаменаци- онный билетВытянули билет
- 40. Вероятность: P(A) = 5/1300 = 1/250.В школе
- 41. Пример 2. При игре в нарды бросают
- 42. Решение Составим следующую таблицуВероятность: P(A)=6/36= =1/6.
- 43. Пример 3.Из карточек составили слово «статистика». Какую
- 44. Всего 10 букв.Буква «с» встречается 2 раза
- 45. Примеры задач на вычисление вероятностей случайных
- 46. Решение задачи №1 ( н а ч
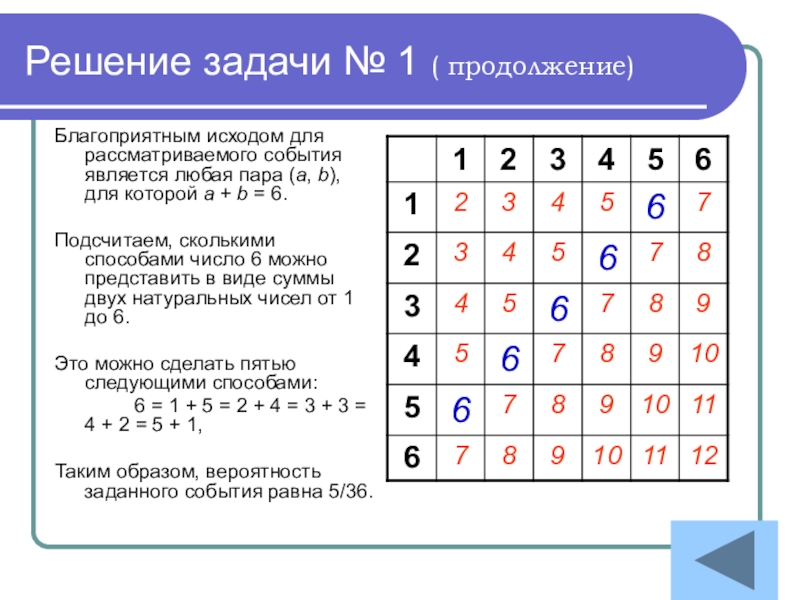
- 47. Решение задачи № 1 ( продолжение)Благоприятным исходом
- 48. Примеры задач на вычисление вероятностей случайных
- 49. Решение задачи №2 (1 способ)
- 50. Решение задачи №2 (2 способ)
- 51. Решение задачи №2 (3 способ)
- 52. Условная вероятность Условной вероятностью события В
- 53. Условная вероятность Формула вычисления вероятности события
- 54. Примеры задач на вычисление вероятностей случайных
- 55. Решение задачи №3 ( н а ч
- 56. Решение задачи №3 ( продолжение)Значит, По условию
- 57. Решение задачи №3 ( продолжение) По условию
- 58. Решение задачи №3 ( окончание)Подставим полученные значения в формулу
Слайд 2Теория и практика
Люди играют с кубиком, в "орла или
Слайд 3Теория и практика
Если подброшенная на ваших глазах реальная монета
Слайд 4Математические модели
математическая модель "монета":
Испытание
выпадение "орла" или "решки "
имеет одинаковую вероятность .
На заре зарождения теории вероятностей были скептики –исследователи, сомневавшиеся в этом вполне очевидном для нас факте и очень много раз подбрасывали монету, но всегда убеждались, что "орел" выпадает в половине случаев.
Статистика
Слайд 5Количество выпадений "орла" при многократном подбрасывания монеты
10 006 раз –
9 996 раз–
для вторых 20 000 бросаний,
20 002 раз–
для всех 40 000 бросаний.
В любом случае частота выпадения
"орла" была очень близка к половине.
Слайд 6Математические модели
математическая модель «игральная кость»:
Это следующий по популярности после монеты случайный эксперимент.
Испытание – подбрасывание кубика; события – выпало 1, 2, 3, 4, 5 или 6 очков (и другие).
выпадение каждой грани
при многократном бросании кубика
имеет одинаковую вероятность .
Слайд 7События и испытания
Предметом исследования в теории вероятностей являются события, появляющиеся при
Каждое осуществление этих условий называют испытанием
Примеры
Слайд 8Примеры испытаний и событий
Испытание – бросание игральной кости
Событие – выпадение шестерки
Испытание – наступление дня
Событие – ясная погода
Слайд 9Вероятность случайного события
Степень объективной возможности случайного события можно измерять
Это число называется
вероятностью случайного события.
Около этого числа группируются относительные частоты данного случайного события
Слайд 11Достоверные события
Событие называется достоверным, если оно наступает всегда,
Вероятность достоверного события всегда равна 1.
Примеры достоверных событий
Слайд 12Примеры достоверных событий
На игральном кубике выпадет меньше семи очков;
После лета наступит
ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
КАМЕНЬ ПАДАЕТ ВНИЗ.
ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ.
Слайд 13Невозможные события
Событие называют невозможным, если оно не наступает никогда,
Вероятность невозможного события равна 0 .
Примеры невозможных событий
Слайд 14Примеры невозможных событий
Падение монеты на ребро
Выпадение на игральной кости семерки
З0
ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.
Слайд 15Случайные события
Событие называется случайным, если при одних и тех
Примеры случайных событий
Слайд 16Примеры случайных событий
Выпадение на игральном кубике четного числа очков;
Выпадение орла при
Выигрышное сочетание чисел на карточках русского лото.
НАЙТИ КЛАД.
БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
В ДОМЕ ЖИВЕТ КОШКА.
Слайд 17Несовместные события
События A и B называются несовместными, если они
Примеры несовместных событий
Слайд 18Примеры несовместных и совместимых событий
совместные события:
идет дождь и идет снег,
человек ест и человек читает,
число целое и четное;
несовместные события:
день и ночь,
человек читает и человек спит
При бросании двух кубиков выпадение нечетной суммы очков и равных чисел на обоих кубиках
Слайд 19Независимые события
События A и B называются независимыми, если вероятность
Примеры независимых событий
Слайд 20Примеры независимых событий
На обоих кубах выпадет шестерка;
При подбрасывании двух монет выпадут
При вытаскивании двух шаров из урны оба шара будут красными.
Слайд 21Противоположные события
С каждым событием A связано противоположное событие, состоящее
Противоположные события, очевидно, несовместны.
Сумма вероятностей противоположных событий равна 1
Примеры противоположных событий
Слайд 22Примеры противоположных событий
На кубике выпадет четное число и на кубике выпадет
Монета упала орлом вверх и монета упала вверх решкой;
Лампа горит и лампа не горит.
если сейчас день, то сейчас не ночь;
если человек спит, то в данный момент он не читает;
если число иррациональное, то оно не является четным.
Слайд 23
Петя задумал натуральное число. Событие состоит в следующем:
а) задумано четное число;
б)
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные, невозможные или случайные.
Слайд 24
Охарактеризуйте следующее событие:
В мешках лежит 10 шаров: 3 синих,
а) из мешка вынули 4 шара и они все синие;
б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара черного
цвета.
Слайд 25ИСХОД
ИСХОДОМ (или элементарным исходом, элементарным событием) называется один
✔
Слайд 26Число возможных исходов в каждом из рассмотренных выше опытах.
Подбрасывание монеты.
–
Подбрасывание кубика.
– 6 исходов: 1, 2, 3, 4, 5, 6.
Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки.
– 3 исхода: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки».
Слайд 27а) В урне четыре шара с номерами два, три, пять, восемь.
б) В копилке лежат три монеты достоинством в 1 рубль, 2 рубля и 5 рублей. Из копилки достают одну монету.
в) В доме девять этажей. Лифт находится на первом этаже. Кто-то из жильцов дома вызывает лифт на свой этаж. Лифтовый диспетчер наблюдает, на каком этаже лифт остановится.
Запишите множество исходов для следующих испытаний
Слайд 28а) За городом N железнодорожные станции расположены в следующем порядке: Луговая,
б) Один ученик записал целое число от 1 до 5, а другой ученик пытается отгадать это число. Событие В – записано чётное число.
в) Вини Пух думает, к кому бы пойти в гости: к Кролику, Пяточку, ослику Иа-Иа или Сове? Событие А – Вини Пух пойдёт к Пяточку; событие В – Вини Пух не пойдёт к Кролику.
Найдите количество возможных исходов.
Слайд 29Действия над событиями
1. Суммой нескольких событий
называется событие,
наступлении хотя бы одного из них в
результате испытания.( , )
Если события А и В совместны, то сумма А+В
означает, что наступает событие А, или событие
В, или оба события вместе.
Если события несовместны, то событие А+В заключается в том, что должны наступить А или В, тогда + заменяется словом «или». .
Слайд 30Действия над событиями
Пример. В урне находятся
красные,
Вынимается один шар. Возможные
события: А – «вынут красный шар», В –
«вынут белый шар», С – « вынут
черный шар».
Тогда А+В означает, что произошло
событие «вынут не черный шар», В+С –
«вынут не красный шар».
Слайд 31Примеры суммы событий:
пусть А - идет дождь, а В - идет
А - пошли на дискотеку; В - пошли в библиотеку, то А + В - пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома.
Слайд 32Действия над событиями
2. Произведением нескольких событий называется событие, состоящие
совместном наступлении всех этих событий в результате испытания.
( ).
Означает союз «и» (АВС, это означает, что
наступило событие А и В и С).
Пример. Пусть имеются следующие события: А – «из колоды карт вынута дама», В – «из колоды карт вынута карта пиковой масти». Значит, А*В означает «вынута дама пик».
Пример. Бросается игральный кубик. Рассмотрим следующие события: А – « число выпавших очков < 5», В – «число выпавших очков > 2», С – «число выпавших очков четное». Тогда А*В*С – «выпало 4 очка».
Слайд 33Примеры произведения событий:
пусть А - из урны вытянули белый шар, В
А - идет дождь, В - идет снег, то АВ - дождь со снегом;
А - число четное, В - число кратное 3, то АВ - число кратное 6.
Слайд 34Задание 3
Опишите, в чем состоит сумма
следующих несовместных
А – учитель вызвал к доске ученика,
В – учитель вызвал к доске ученицу, А+В –.
учитель вызвал к доске ученика или ученицу
Родила царица в ночь:
А – не то сына,
В – не то дочь
А+В – царица родила сына или дочь.
Слайд 35Диаграммы Венна
Графические изображения на плоскости соотношений между множествами называются
Слайд 36Дополнительные задания
Задание 4. Из событий:
2) «сегодня по расписанию шесть уроков»;
3) «сегодня первое января»;
4) «температура воздуха в Салехарде +20°С» - составить все возможные пары и выявить среди них пары совместных и пары несовместных событий.
Задание 5. Из полной колоды карт вынимается одна карта. Выяснить, являются совместными или несовместными события:
«вынута карта красной масти» и «вынут валет»;
«вынут король» и «вынут туз».
Слайд 37Вопросы
Могут ли события быть одновременно и несовместными и совместными?
Входит ли в
Задание.
Укажите события, противоположные данным: а) на кубике выпало 1; б) Света получила на экзамене «5»; в) после ночи наступает утро?
Слайд 38 Вероятностью Р наступления случайного события А называется отношение
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Слайд 39Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем кубик
На кубике выпало
6
3
Играем в лотерею
Выиграли, купив один билет
250
10
Слайд 40Вероятность:
P(A) = 5/1300 = 1/250.
В школе 1300 человек, из
Какова вероятность того, что один из них попадётся директору на глаза?
Слайд 41Пример 2.
При игре в нарды бросают 2 игральных кубика. Какова
Слайд 43
Пример 3.
Из карточек составили слово «статистика». Какую карточку с буквой вероятнее
с
т
а
т
и
с
т
и
к
а
Слайд 44Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10
буква «т» встречается 3 раза –
P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение
Слайд 45Примеры задач на вычисление
вероятностей случайных событий
З а д
Бросаются два кубика. Найти вероятность того, что сумма выпавших очков равна 6.
Р е ш е н и е .
Слайд 46Решение задачи №1 ( н а ч а л о)
Результат каждого бросания – это пара чисел (a, b), где a и b – числа от 1 до 6. Поэтому все поле событий состоит из 6х6 = 36 элементов
Слайд 47Решение задачи № 1 ( продолжение)
Благоприятным исходом для рассматриваемого события является
Подсчитаем, сколькими способами число 6 можно представить в виде суммы двух натуральных чисел от 1 до 6.
Это можно сделать пятью следующими способами:
6 = 1 + 5 = 2 + 4 = 3 + 3 = 4 + 2 = 5 + 1,
Таким образом, вероятность заданного события равна 5/36.
Слайд 48Примеры задач на вычисление
вероятностей случайных событий
З а д
Один стрелок делает 80% попаданий, а другой (при тех же условиях стрельбы) 70%. Найти вероятность поражения цели, если оба стрелка стреляют в нее одновременно. Цель считается пораженной при попадании в нее хотя бы одной их двух пуль.
Р е ш е н и е (1 способ)
Р е ш е н и е (2 способ)
Р е ш е н и е (3 способ)
Слайд 49Решение задачи №2 (1 способ)
Один стрелок делает 80%
Допустим, что производится 100 двойных выстрелов. Примерно в 80 из них цель будет поражена первым стрелком. Остается около 20 выстрелов, в которых этот стрелок даст промах. Так как второй стрелок поражает в среднем 70 раз из 100 выстрелов и, значит, 7 раз из 10 выстрелов, то мы можем ожидать, что в тех 20 выстрелах, в которых первый стрелок даст промах, второму удастся поразить цель примерно 14 раз. Таким образом, при всей сотне выстрелов цель окажется пораженной 80 + 14 = 94 раза. Вероятность поражения цели при одновременной стрельбе этих двух стрелков равна поэтому 94%, или 0,94.
Слайд 50Решение задачи №2 (2 способ)
Один стрелок делает 80%
Вероятность попадания
Первого стрелка 0,8
Второго стрелка 0,7
Вероятность не попадания
Первого стрелка 1 - 0,8 = 0,2
Второго стрелка 1 - 0,7 = 0,3
Цель будет поражена, если
первый стрелок попадет, а второй нет 0,8∙0,3 = 0,24
второй стрелок попадет, а первый нет 0,7∙0,2 = 0,14
оба стрелка попадут 0,8∙0,7 = 0,56
Значит, цель будет поражена с вероятностью
0,24 + 0,14 + 0,56 = 0,94
Слайд 51Решение задачи №2 (3 способ)
Один стрелок делает 80%
Вероятность попадания
Первого стрелка 0,8
Второго стрелка 0,7
Вероятность не попадания
Первого стрелка 1 - 0,8 = 0,2
Второго стрелка 1 - 0,7 = 0,3
Цель не будет поражена, если
оба стрелка не попадут 0,2∙0,3 = 0,06
Значит, цель будет поражена с вероятностью
1 - 0,06 = 0,94
Слайд 52Условная вероятность
Условной вероятностью события В при условии А называют
Вероятность события В в новых условиях: когда уже известно, что событие А произошло.
Слайд 53Условная вероятность
Формула вычисления вероятности
события В при условии, что
событие А, но могло иметь место еще и событие С.
Пример использования такой обобщенной формулы
рассмотрен далее.
Слайд 54Примеры задач на вычисление
вероятностей случайных событий
З а д а ч
Пусть в некотором классе 25 учеников, из них
2 "отличника",
12 "твердых хорошистов",
9 "троечников",
а остальные 2 – "отстающие".
Проверяя контрольную работу, учитель поставил 5 за одну работу, которая оказалась неподписанной. Прав ли он, считая, что она принадлежит "отличнику", если вероятность получения пятерки соответственно равна:
Отличник 0,9
Хорошист 0,7
Троечник 0,3
Отстающий 0,1?
Р е ш е н и е .
Слайд 55Решение задачи №3 ( н а ч а л о)
где B – событие, при котором неподписанная работа принадлежит одному из отличников .
буквами C, D, E обозначены события, при которых
пятерку получил соответственно
"хорошист", "троечник" и "отстающий".
Слайд 56Решение задачи №3 ( продолжение)
Значит,
По условию
Из 25 учеников
2 "отличника",
"хорошистов",
9 "троечников",
2 "отстающие".
Неподписанная работа принадлежит
B - одному из отличников ,
С - одному из хорошистов ,
D - одному из троечников ,
E - одному из отстающих .
Слайд 57Решение задачи №3 ( продолжение)
По условию
Из 25 учеников
2 "отличника",
"хорошистов",
9 "троечников",
2 "отстающие".
Неподписанная работа принадлежит
B - одному из отличников ,
С - одному из хорошистов ,
D - одному из троечников ,
E - одному из отстающих .
Учитывая то, что анонимную работу написал только один ученик, рассмотрим вероятность того, что
работу написал отличник,
а не хорошист, не троечник и не отстающий
работу написал хорошист,
работу написал троечник,
работу написал отстающий.