- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теория вероятностей
Содержание
- 1. Презентация по математике на тему Теория вероятностей
- 2. Решение. 1) 60 – 3 = 57 вопросов Андрей выучил .
- 3. Задание 2 В фирме такси в
- 4. Задание 3 На тарелке 16 пирожков:
- 5. ↑ Задание 4 В случайном эксперименте бросают
- 6. ↑ Задание 5 В случайном эксперименте симметричную
- 7. Задание 6 В чемпионате по гимнастике
- 8. Задание 7 При производстве в
- 9. Задание 8 Фабрика выпускает сумки. В
- 10. Задание 9 В соревнованиях по толканию
- 11. Задание 10 Фабрика выпускает сумки. В
- 12. Задание 11 Научная конференция проводится в
- 13. Задание 12 Конкурс исполнителей проводится в 5
- 14. Задание 13 На конференцию приехали 3
- 15. Задание 24 В случайном эксперименте симметричную
- 16. Задание 25 На рокфестивале выступают группы
- 17. Задание 26 В некотором городе из
- 18. Задание 27 На борту самолёта 12
- 19. Задание 28 На олимпиаде по русскому
- 20. Задание 29 В классе 26 учащихся,
- 21. Задание 30 В фирме такси в
- 22. Задание 31 В группе туристов 30
Слайд 2Решение. 1) 60 – 3 = 57 вопросов Андрей выучил . 2) Вероятность того, что
Задание 1
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Слайд 3Задание 2 В фирме такси в данный момент свободно 20 машин:
Решение.
Вероятность того, что к заказчице приедет зеленое такси равна 8:20=0,4 .
Ответ: 0,4.
Слайд 4Задание 3 На тарелке 16 пирожков: 7 с рыбой, 5 с
Решение.
Вероятность того, что пирожок окажется с вишней равна 4:16=0,25 .
Ответ: 0,25.
Слайд 5↑ Задание 4 В случайном эксперименте бросают две игральные кости. Найдите вероятность
Решение.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5:
2+6,
3+5,
4+4,
5+3,
6+2.
Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна 5:36=0,138 Ответ: 0,14.
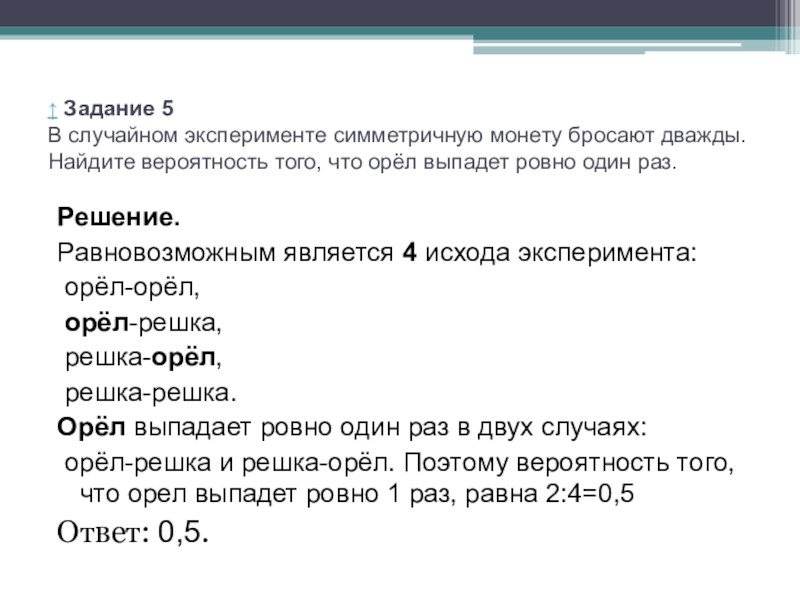
Слайд 6↑ Задание 5 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
Решение.
Равновозможным является 4 исхода эксперимента:
орёл-орёл,
орёл-решка,
решка-орёл,
решка-решка.
Орёл выпадает ровно один раз в двух случаях:
орёл-решка и решка-орёл. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна 2:4=0,5
Ответ: 0,5.
Слайд 7Задание 6 В чемпионате по гимнастике участвуют 20 спортсменок: 8 из
Решение.
В чемпионате принимает участие 20 − (8 + 7) = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5:20=0,25
Ответ: 0,25.
Слайд 8Задание 7 При производстве в среднем на каждые 2982 исправных насоса
Решение.
В среднем неисправных 18 из каждых 3000 насосов, поэтому вероятность случайно выбрать неисправный насос равна 18:3000=0,006
Ответ: 0,006
Слайд 9Задание 8 Фабрика выпускает сумки. В среднем 8 сумок из 100
Решение.
В среднем без дефектов выпускают 92 сумки из каждых 100, поэтому искомая вероятность равна 92:100=0,92.
Ответ: 0, 92.
Слайд 10Задание 9 В соревнованиях по толканию ядра участвуют 4 спортсмена из
Решение.
Всего в соревнованиях принимает участие 4 + 7 + 9 + 5 = 25 спортсменов.
Значит, вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна 9:25=0,36
Ответ: 0,36.
Слайд 11Задание 10 Фабрика выпускает сумки. В среднем 11 сумок из 160
Решение.
По условию, качественных сумок в среднем 149 из 160. Значит, вероятность того, что купленная сумка окажется качественной, равна 149:160=0,931…=0,93
Ответ: 0,93.
Слайд 12Задание 11 Научная конференция проводится в 5 дней. Всего запланировано 75
Решение.
За первые три дня будет прочитан 3∙17=51 доклад,
на последние два дня планируется 75-51=24 доклада.
Поэтому на последний день запланировано 24:2=12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12:75=0,16
Ответ: 0,16.
Слайд 13Задание 12 Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений
Решение.
На третий день запланировано
(80-8):4=18 выступлений.
Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
18:80=0,225
Ответ: 0,225.
Слайд 14Задание 13 На конференцию приехали 3 ученых из Норвегии, 3 из
Решение.
Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым(десятым, первым неважно!), окажется из России, равна 3:10 = 0,3.
Ответ: 0,3.
Слайд 15Задание 24 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
Решение.
Всего возможных исходов — четыре:
орел-орел,
орел-решка,
решка-орел,
решка-решка.
Благоприятным является один: орел-решка. Следовательно, искомая вероятность равна 1 : 4 = 0,25.
Ответ: 0,25.
Слайд 16Задание 25 На рокфестивале выступают группы — по одной от каждой
Решение.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих
(Д — Дания, Ш — Швеция, Н — Норвегия):
Д...Ш...Н...,
Д...Н...Ш...,
Ш...Н...Д...,
Ш...Д...Н...,
Н...Д...Ш...,
Н...Ш...Д...
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна 2:6=0,33…
Ответ: 0,33.
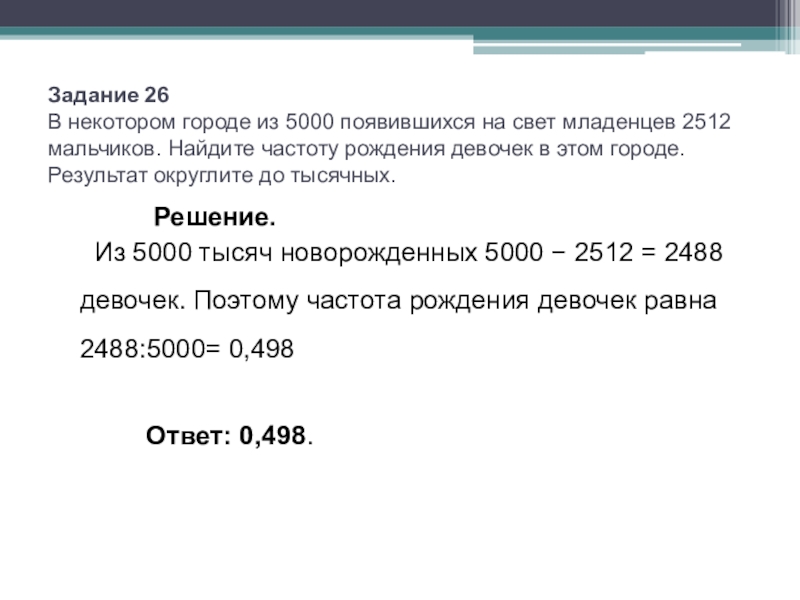
Слайд 17Задание 26 В некотором городе из 5000 появившихся на свет младенцев
Решение.
Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна 2488:5000= 0,498
Ответ: 0,498.
Слайд 18Задание 27 На борту самолёта 12 кресел расположены рядом с запасными
Решение.
В самолете 12 + 18 = 30 мест удобны пассажиру В., а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30 : 300 = 0,1.
Ответ: 0,1.
Слайд 19Задание 28 На олимпиаде по русскому языку 250 участников разместили в
Решение.
Всего в запасную аудиторию направили
250 − 120 − 120 = 10 человек.
Поэтому вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна 10 : 250 = 0,04.
Ответ: 0,04.
Слайд 20Задание 29 В классе 26 учащихся, среди них два друга —
Решение.
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй друг окажется среди этих 12 человек, равна 12 : 25 = 0,48.
Ответ: 0,48
Слайд 21Задание 30 В фирме такси в наличии 50 легковых автомобилей; 27
Решение.
Машин желтого цвета с черными надписями 23, всего машин 50. Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета с черными надписями, равна: 23:50=0,46
Ответ: 0,46.
Слайд 22Задание 31 В группе туристов 30 человек. Их вертолётом в несколько
Решение.
На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист П. полетит первым рейсом вертолёта, равна:
6:30=0,2
Ответ : 0,2