Способы решения квадратных уравнений
8класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Способы решения квадратных уравнений
Содержание
- 1. Презентация по математике на тему Способы решения квадратных уравнений
- 2. 1. Систематизировать и обобщить знания, умения и
- 3. Способы решения квадратного уравнения1 способ: решение квадратного
- 4. Способы решения квадратного уравнения3 способ: используя теорему Виета.4 способ: Свойство коэффициентов квадратного уравнения.
- 5. Способы решения квадратного уравнения5 способ: Графически.6 способ: Метод выделения полного квадрата.
- 6. Рассмотрим примеры решения квадратного уравнения, используя свойства коэффициентов.
- 7. Решая квадратное уравнение графически, возможны три случая:1.
- 8. 1.Решим графически уравнение х2 - 3х -
- 9. 2.Решим графически уравнение х2 - 2х +
- 10. 3) Решим графически уравнение х2 - 2х
- 11. Решим квадратное уравнение по теореме обратной теореме Виета
- 12. Оцени свою работу на уроке:
- 13. Слайд 13
1. Систематизировать и обобщить знания, умения и навыки решать квадратные уравнения.2. Обобщить представление о способах решения квадратных уравнений.Цель урока:
Слайд 1Учитель: Кузема Надежда Николаевна,
Алтайский краевой педагогический лицей – интернаТ (ЦДО),
Барнаул, 2019
Тема:
Слайд 21. Систематизировать и обобщить знания, умения и навыки решать квадратные уравнения.
2.
Обобщить представление о способах решения квадратных уравнений.
Цель урока:
Слайд 3Способы решения квадратного уравнения
1 способ: решение квадратного уравнения по формуле
2 способ:
Разложение левой части уравнения на множители
Слайд 4Способы решения квадратного уравнения
3 способ: используя теорему Виета.
4 способ: Свойство коэффициентов
квадратного уравнения.
Слайд 5Способы решения квадратного уравнения
5 способ: Графически.
6 способ: Метод выделения полного квадрата.
Слайд 7Решая квадратное уравнение графически, возможны три случая:
1. Прямая и парабола могут
пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
2. Прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
3. Прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
2. Прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
3. Прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
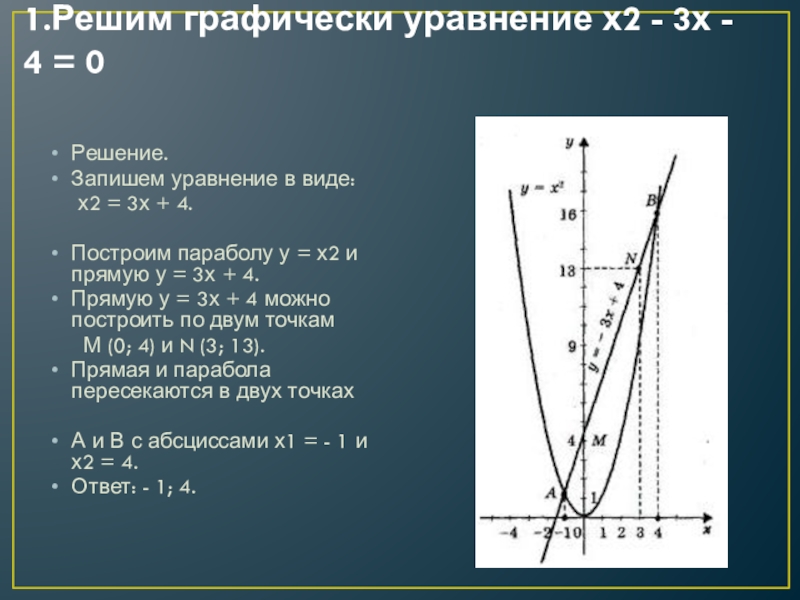
Слайд 81.Решим графически уравнение х2 - 3х - 4 = 0
Решение.
Запишем
уравнение в виде:
х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам
М (0; 4) и N (3; 13).
Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = - 1 и х2 = 4.
Ответ: - 1; 4.
х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам
М (0; 4) и N (3; 13).
Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = - 1 и х2 = 4.
Ответ: - 1; 4.
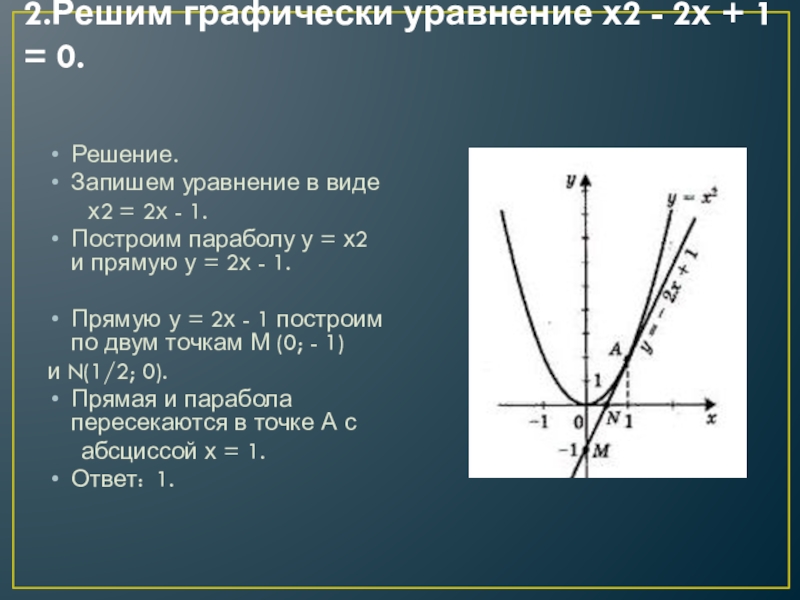
Слайд 92.Решим графически уравнение х2 - 2х + 1 = 0.
Решение.
Запишем
уравнение в виде
х2 = 2х - 1.
Построим параболу у = х2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N(1/2; 0).
Прямая и парабола пересекаются в точке А с
абсциссой х = 1.
Ответ: 1.
х2 = 2х - 1.
Построим параболу у = х2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N(1/2; 0).
Прямая и парабола пересекаются в точке А с
абсциссой х = 1.
Ответ: 1.
Слайд 103) Решим графически уравнение х2 - 2х + 5 = 0
Решение.
Запишем уравнение в виде х2 = 5х - 5.
Построим параболу у = х2 и прямую у = 2х - 5.
Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0).
Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 - 2х + 5 = 0 корней не имеет.