- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Производная
Содержание
- 1. Презентация по математике на тему Производная
- 2. Определение производной.Физический смысл производной.Геометрический смысл производной.Основные правила
- 3. Определение производнойПусть на некотором интервале (a, b)
- 4. Геометрический смысл производной Пусть функция y= f(x)
- 5. Физический смысл производной 1. Задача об
- 6. 2. ЗАДАЧА О СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ
- 7. АЛГОРИТМ вычисления производнойПроизводная функции y= f(x) может
- 8. Основные правила дифференцированияПусть u=u(x) и v=v(x) –
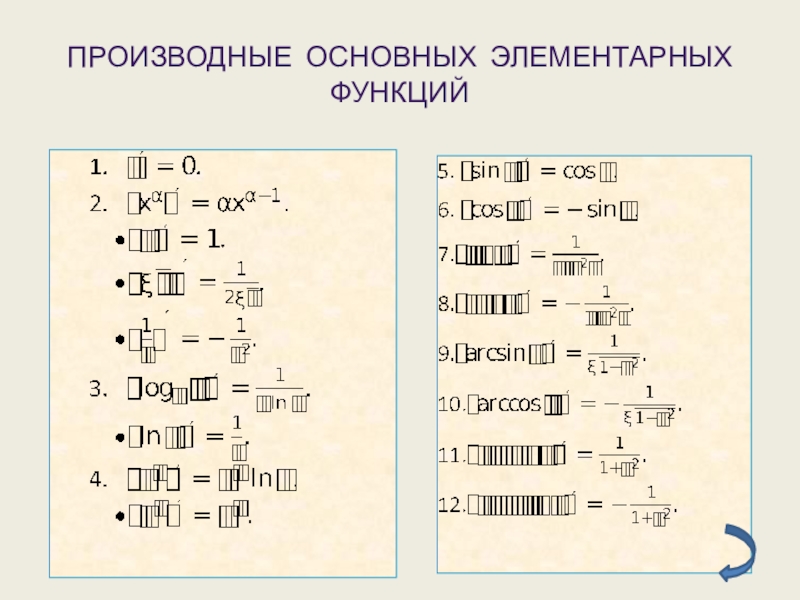
- 9. Производные основных элементарных функций
- 10. Производная сложной функцииТеорема. Если функция
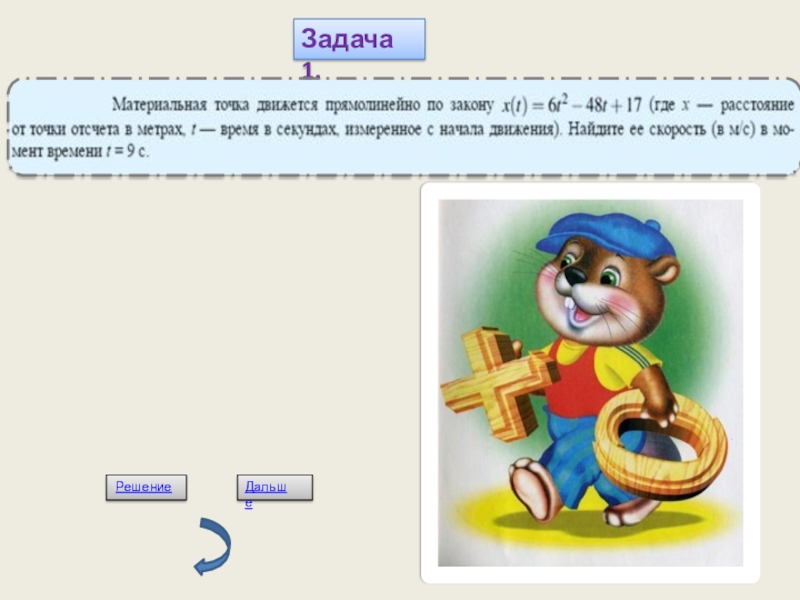
- 11. Задача 1.
- 12. Слайд 12
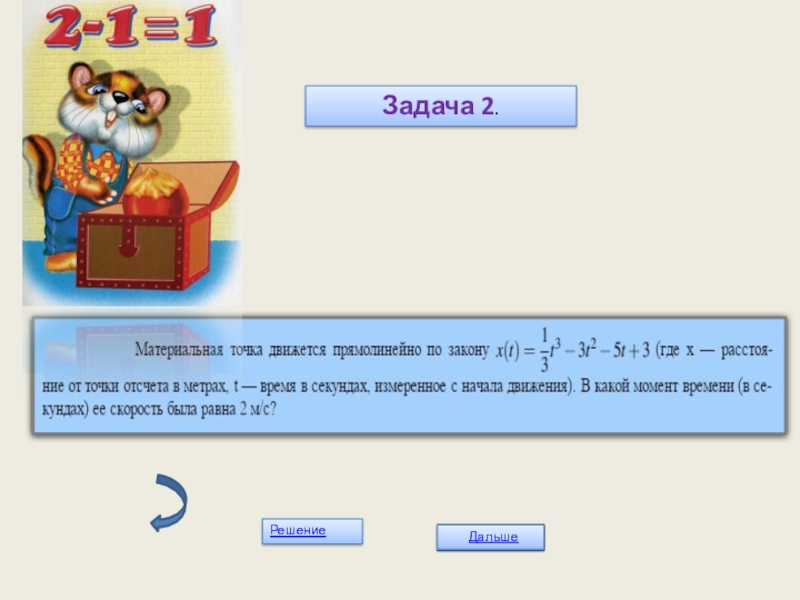
- 13. Задача 2.
- 14. .
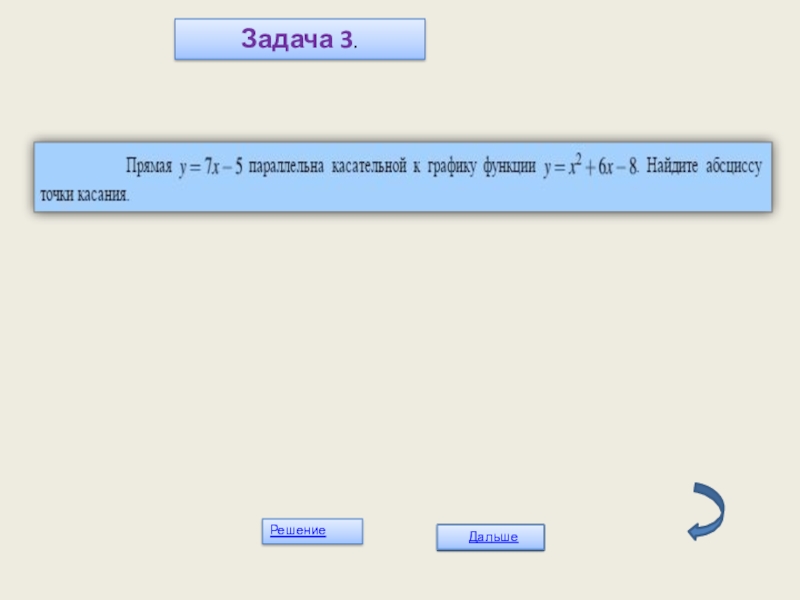
- 15. Задача 3.
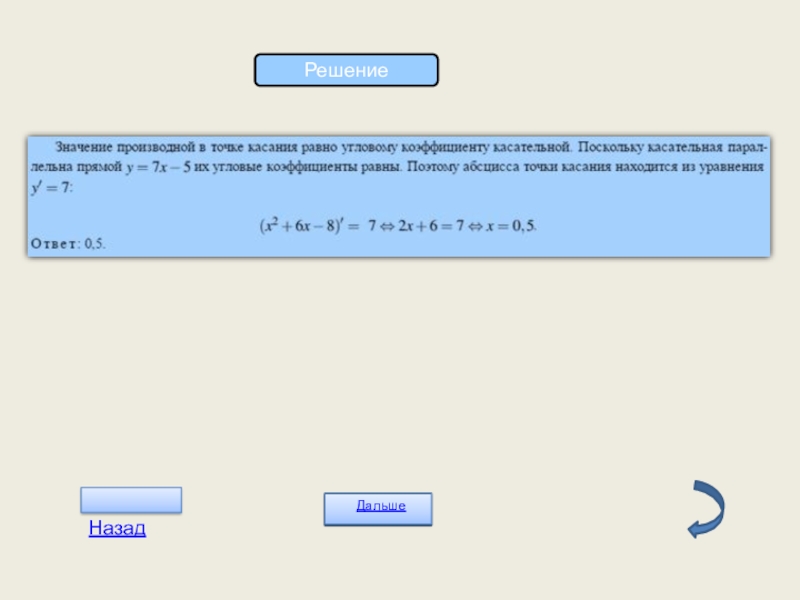
- 16. Решение
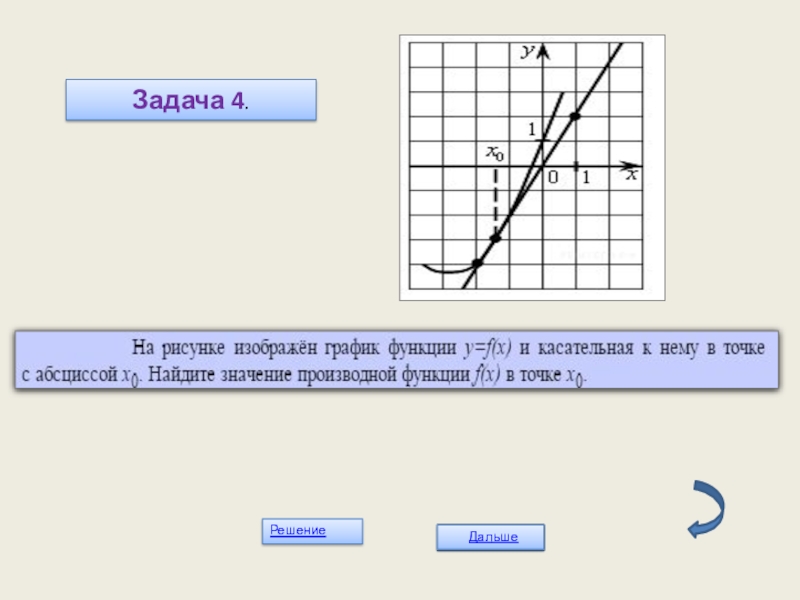
- 17. Задача 4.
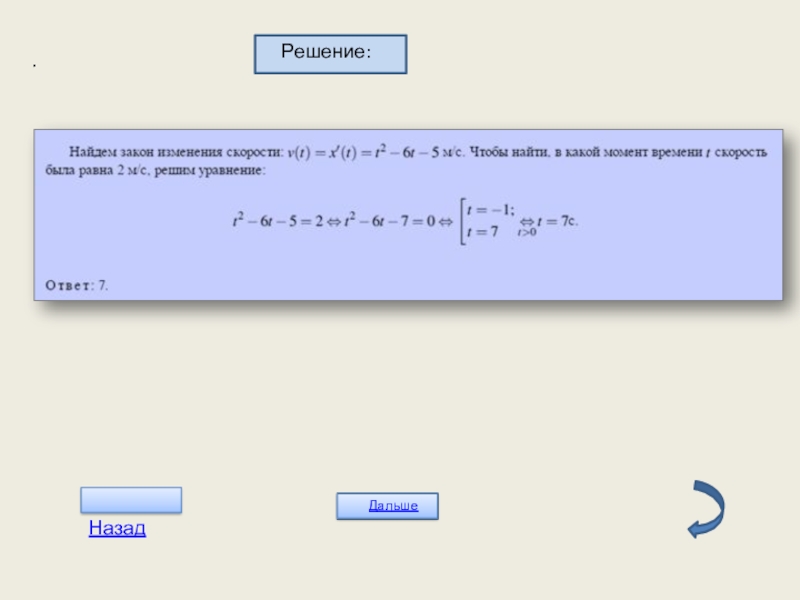
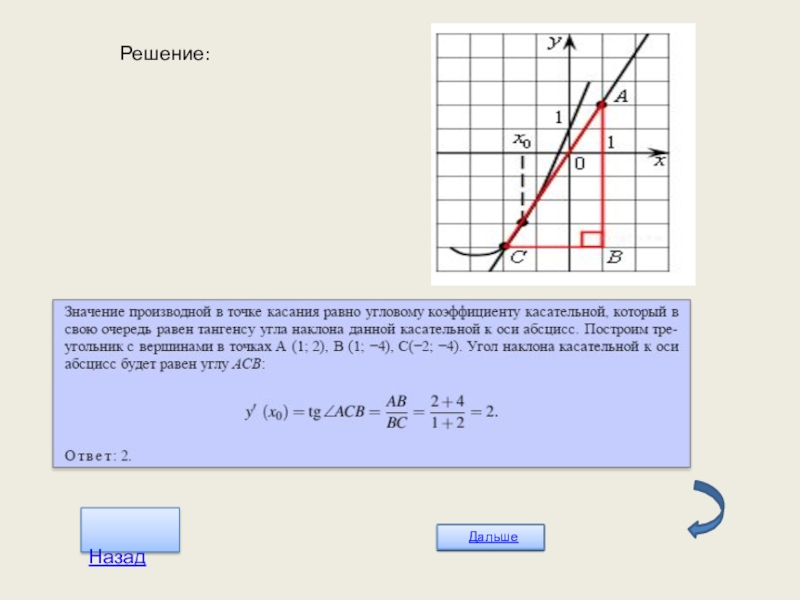
- 18. Решение:
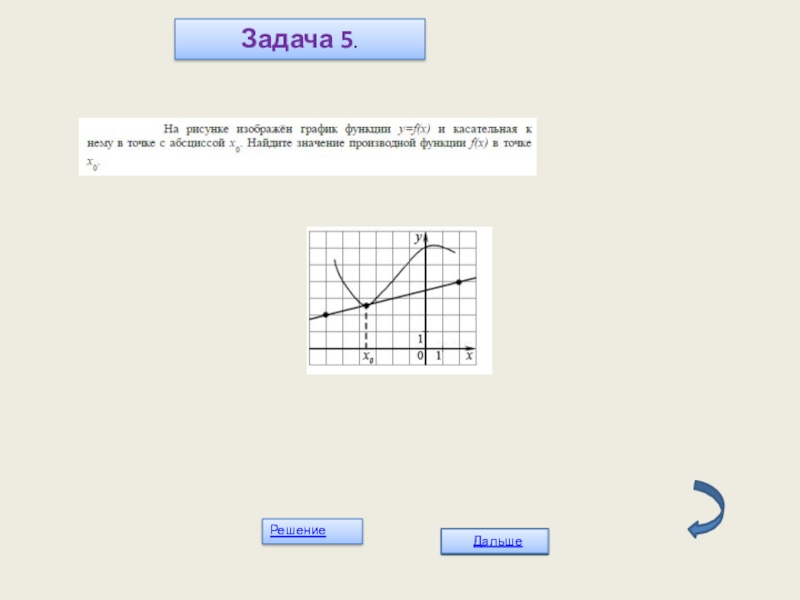
- 19. Задача 5.
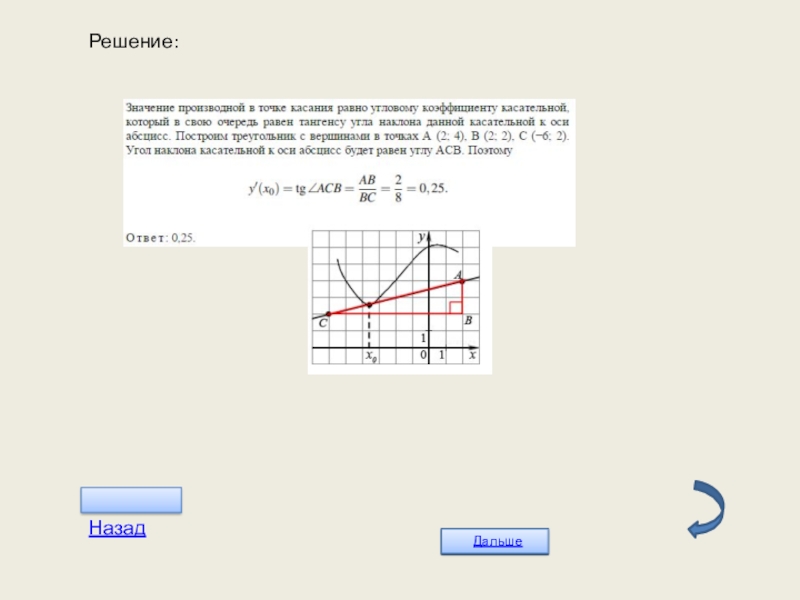
- 20. Решение:
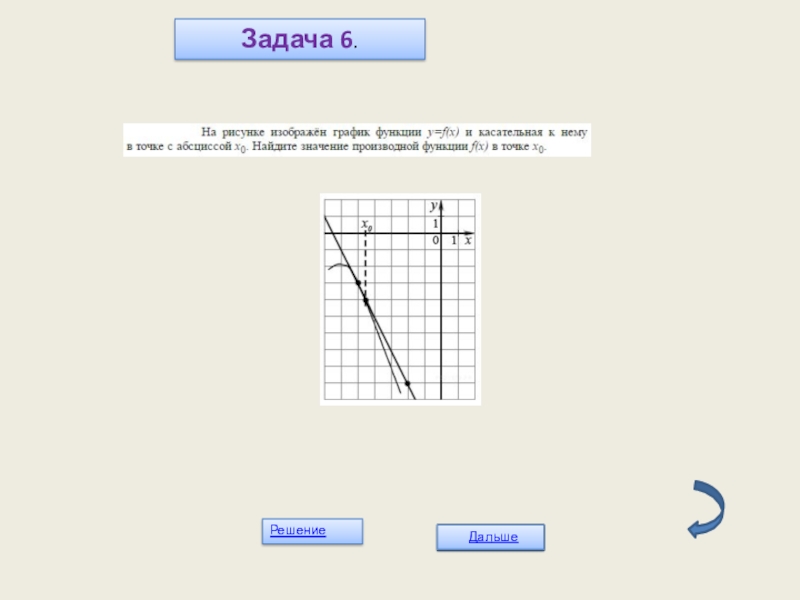
- 21. Задача 6.
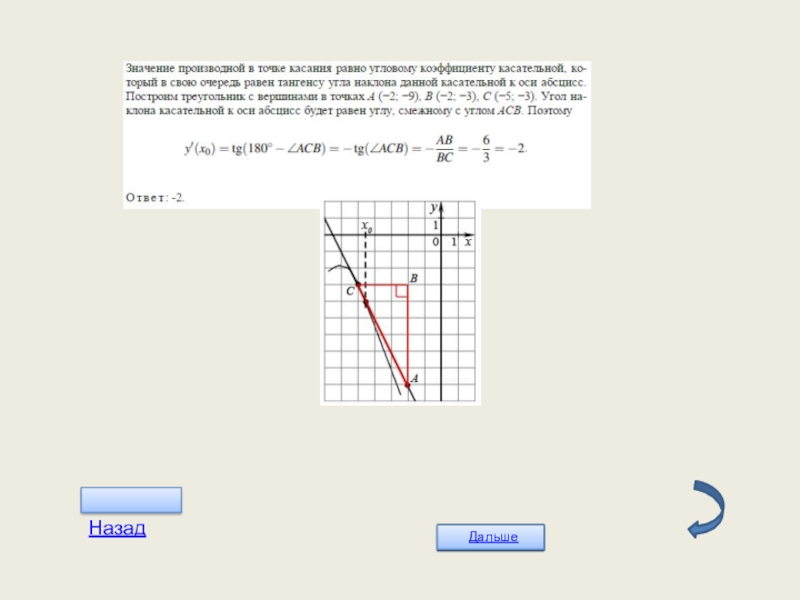
- 22. Слайд 22
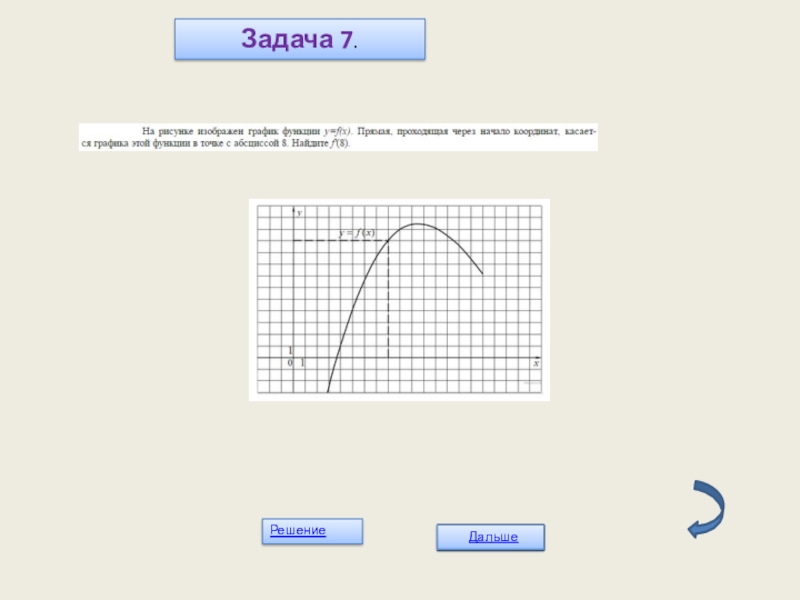
- 23. Задача 7.
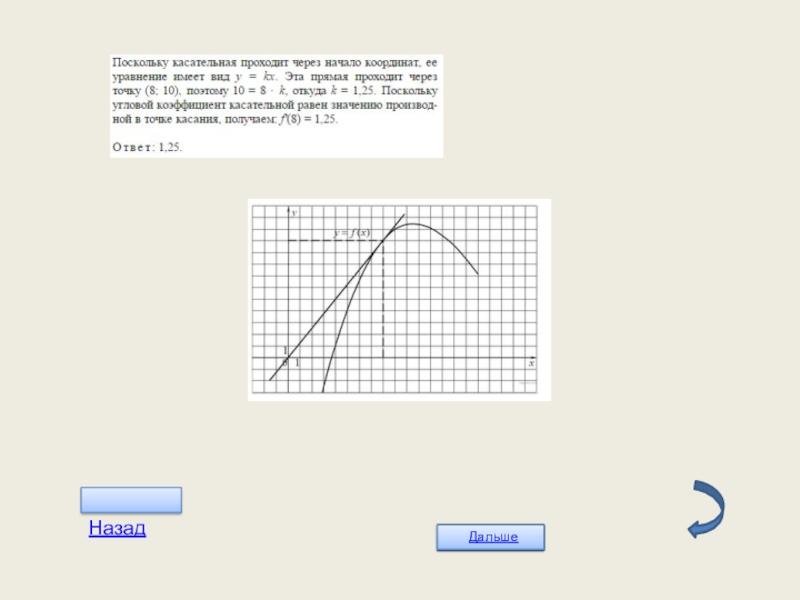
- 24. Слайд 24
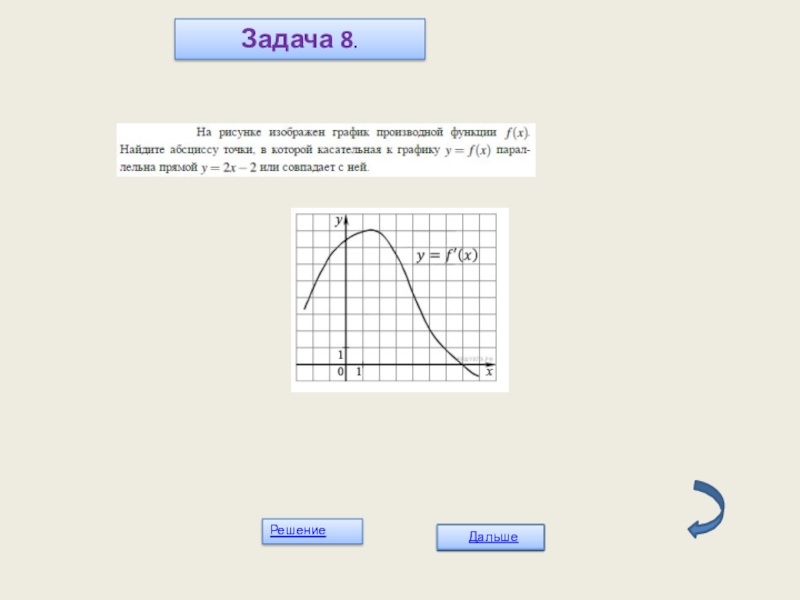
- 25. Задача 8.
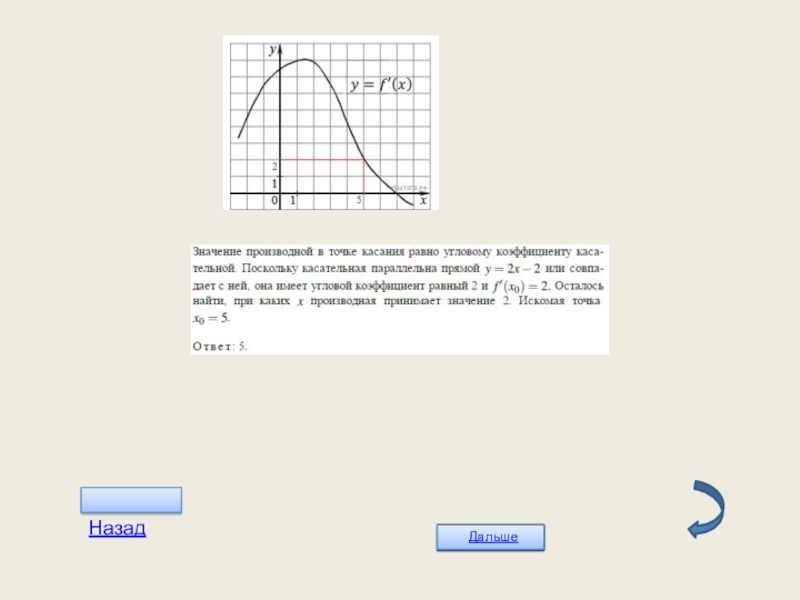
- 26. Слайд 26
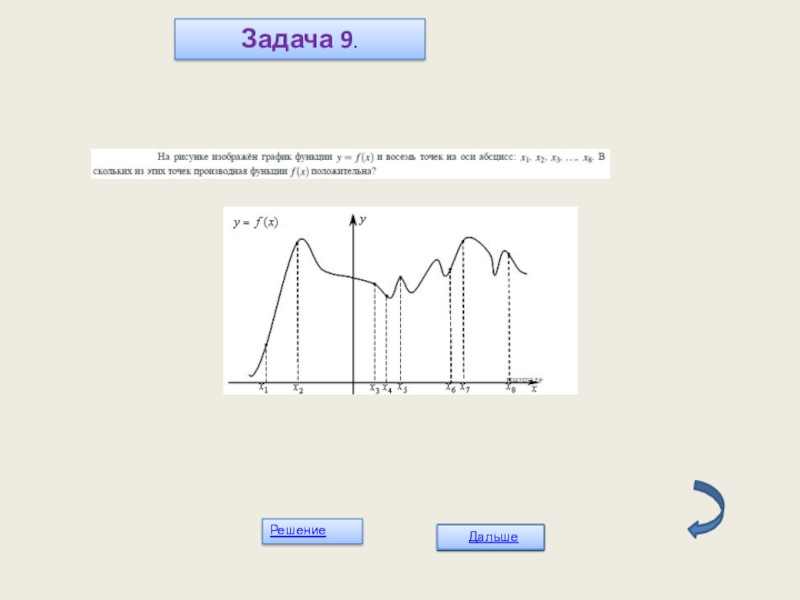
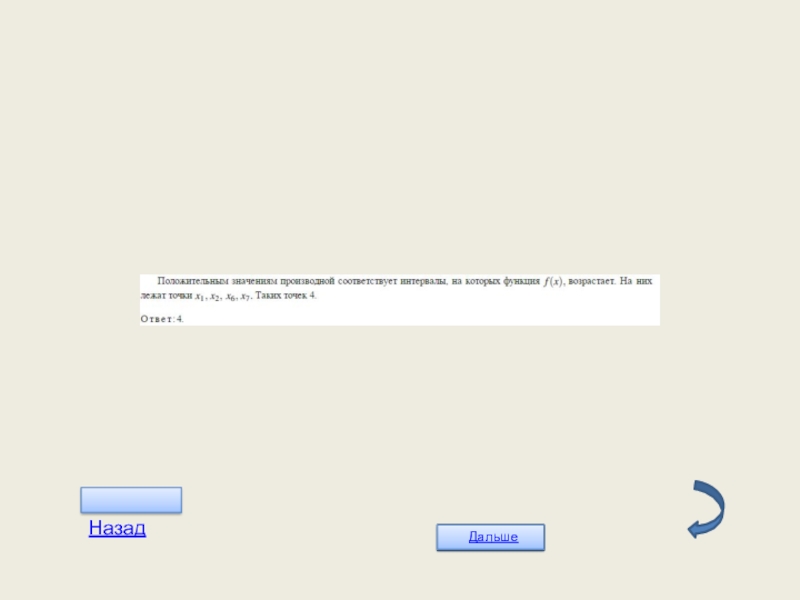
- 27. Задача 9.
- 28. Слайд 28
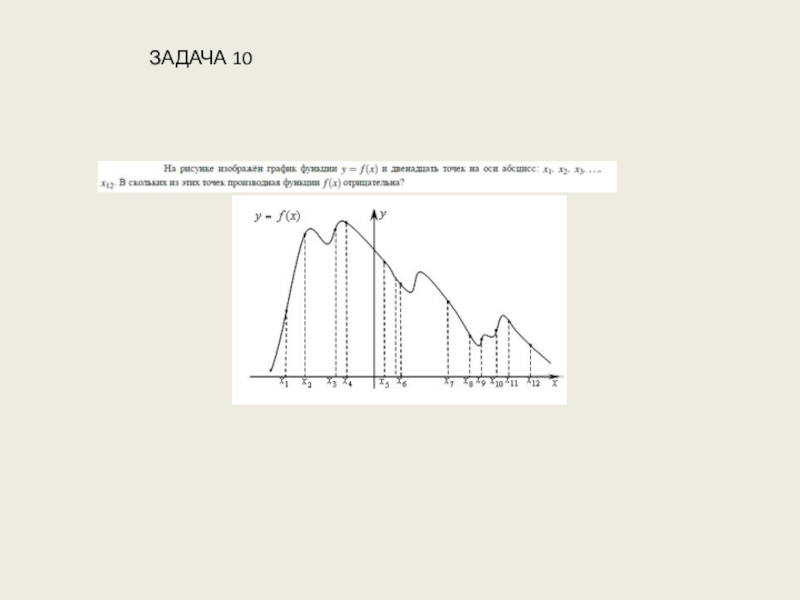
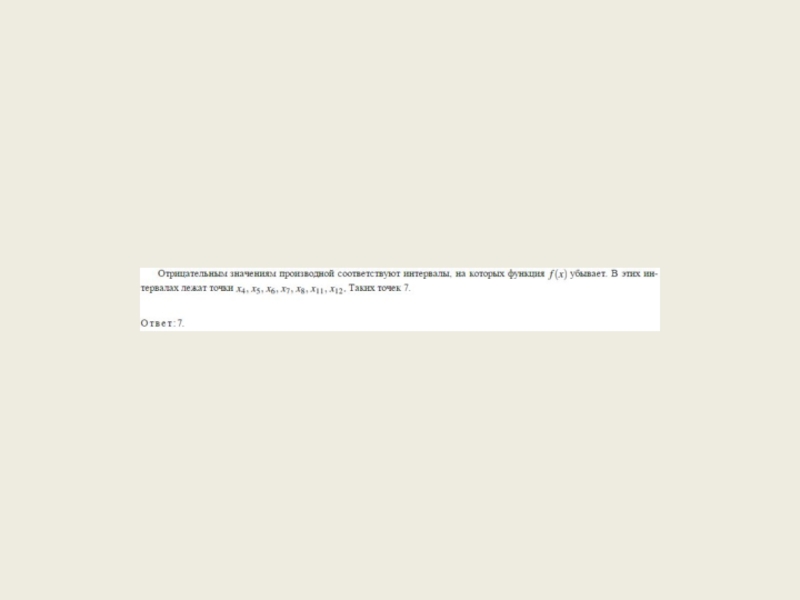
- 29. ЗАДАЧА 10
- 30. Слайд 30
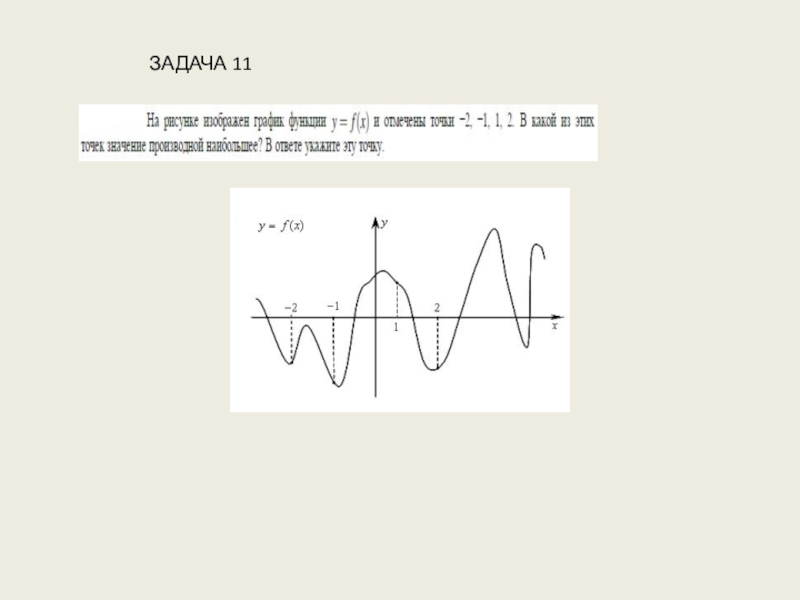
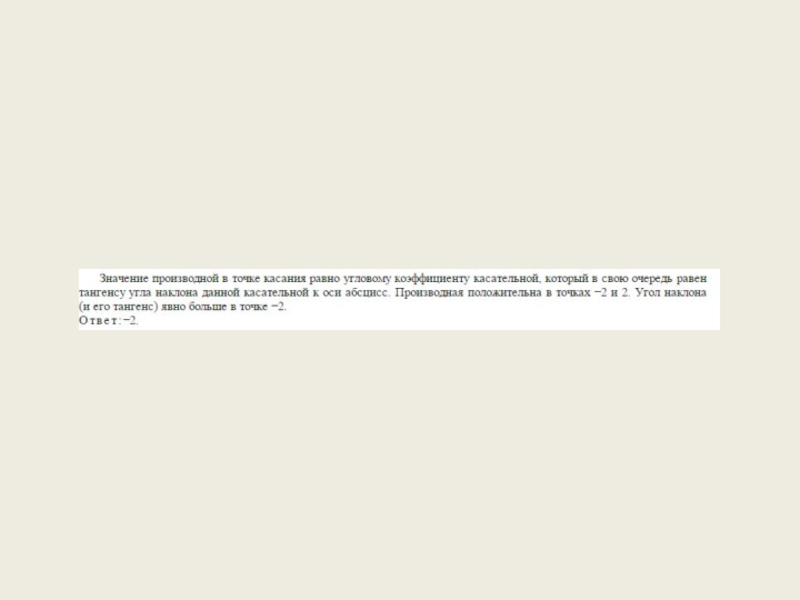
- 31. ЗАДАЧА 11
- 32. Слайд 32
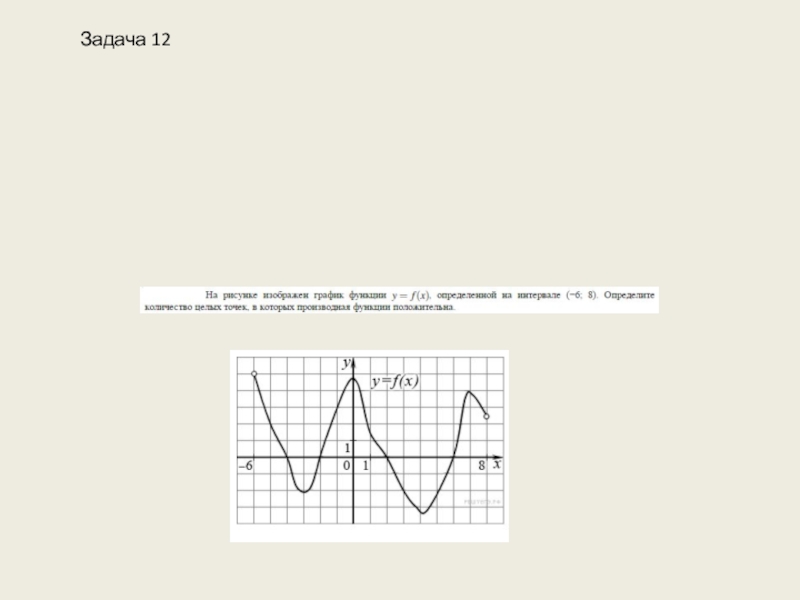
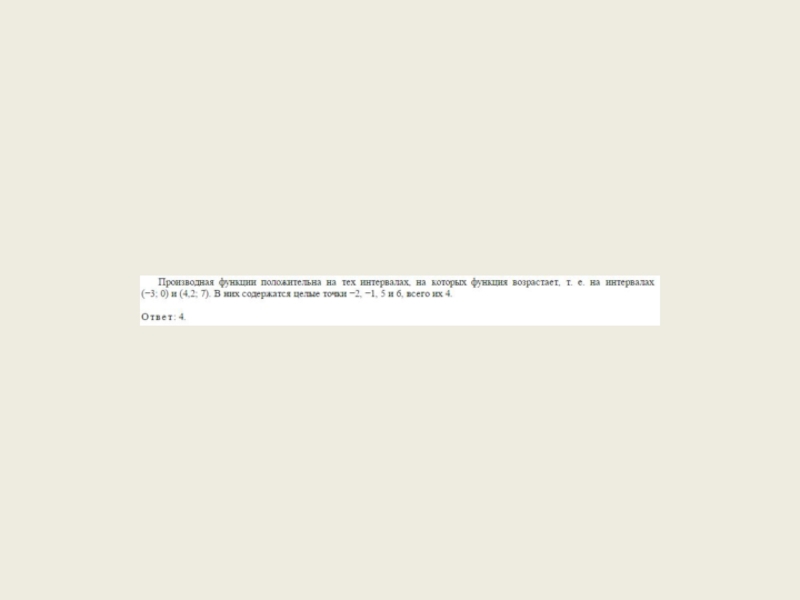
- 33. Задача 12
- 34. Слайд 34
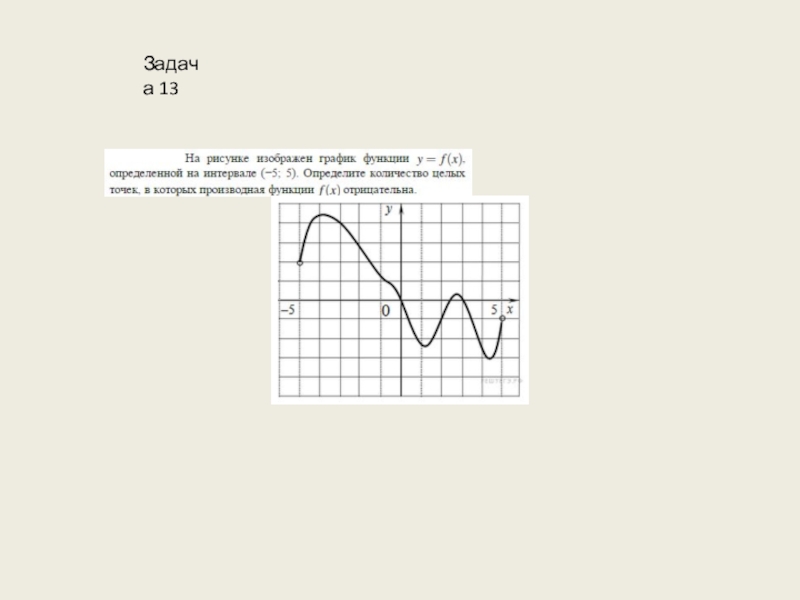
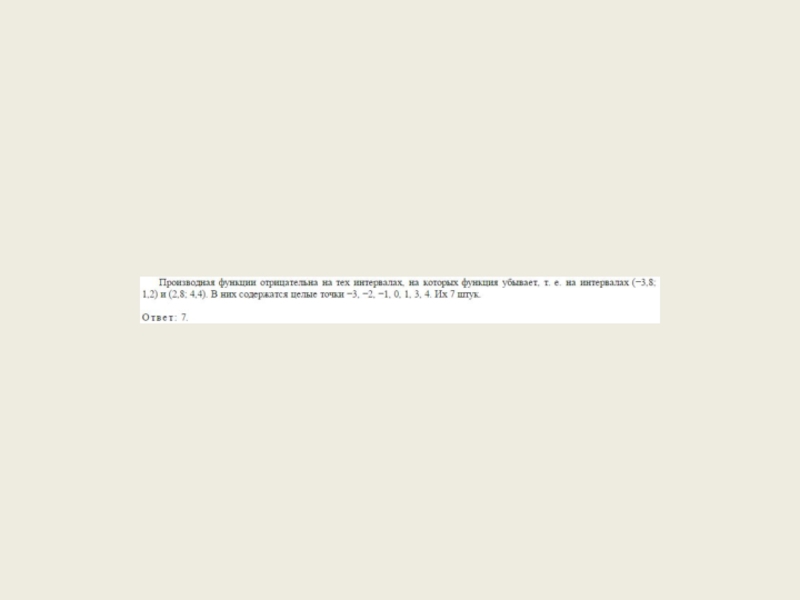
- 35. Задача 13
- 36. Слайд 36
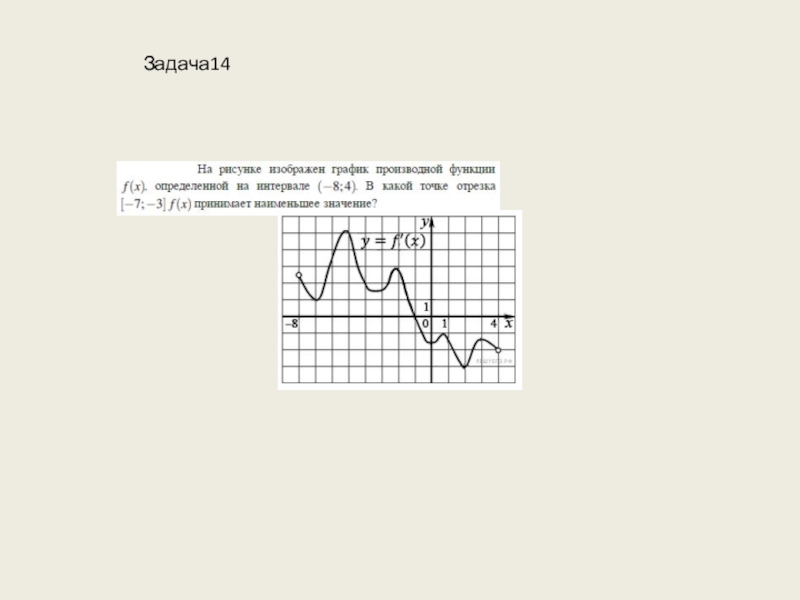
- 37. Задача14
- 38. Слайд 38
- 39. Слайд 39
Слайд 2Определение производной.
Физический смысл производной.
Геометрический смысл производной.
Основные правила дифференцирования.
Производные основных элементарных функций.
Производная
Примеры решения задач по теме производная.
Слайд 3Определение производной
Пусть на некотором интервале (a, b) определена функция y= f(x).
Производной функции y=f(x) в точке x =x0 называется предел отношения приращения функции ∆y в этой точке к приращению аргумента ∆x, при стремлении приращения аргумента к нулю.
Слайд 4Геометрический смысл производной
Пусть функция y= f(x) определена на некотором промежутке (a,
y
͢͢
α
β
Где - угол наклона касательной функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой:
Слайд 5Физический смысл производной
1. Задача об определении скорости движения материальной частицы
Пусть вдоль
К моменту времени t0 пройденный путь равен s0 = s(t0), а к моменту (t0 +∆t) – путь s0 + ∆s=s(t0 +∆t).
Тогда за промежуток ∆t средняя скорость будет
Чем меньше ∆t, тем лучше средняя скорость характеризует движение точки в момент t0. Поэтому под скоростью точки в момент t0 следует понимать предел средней скорости за промежуток от t0 до t0 +∆t, когда ∆t⇾0 , т.е.
Слайд 62. ЗАДАЧА О СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ
Пусть некоторое
- скорость химической реакции в данный момент
времени t.
3. ЗАДАЧА ОПРЕДЕЛЕНИЯ СКОРОСТИ РАДИОАКТИВНОГО РАСПАДА
Если m- масса радиоактивного вещества и t- время, то явление радиоактивного распада в момент времени t при условии, что масса радиоактивного вещества с течением времени уменьшается, характеризуется функцией m= m(t).
Средняя скорость распада за время ∆t выражается отношением
а мгновенная скорость распада в момент времени t
.
Слайд 7АЛГОРИТМ вычисления производной
Производная функции y= f(x) может быть найдена по следующей
1. Дадим аргументу x приращение ∆x≠0 и найдем наращенное значение функции y+∆y= f(x+∆x).
2. Находим приращение функции ∆y= f(x+∆x) - f(x).
3. Составляем отношение
4. Находим предел этого отношения при ∆x⇾0, т.е.
( если этот предел существует).
Слайд 8Основные правила дифференцирования
Пусть u=u(x) и v=v(x) – дифференцируемые функции в точке
1) (u v) = u v
2) (uv) = uv +uv
(cu) = cu
3) , если v 0
Слайд 10Производная сложной функции
Теорема. Если функция
дифференцируема в соответствующей точке , то сложная функция дифференцируема в точке x, причем:
т.е. производная сложной функции равна произведению производной функции по промежуточному аргументу на производную промежуточного аргумента по x.