Романова Н.Е.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Подготовка к ОГЭ 2017. Задача №26
Содержание
- 1. Презентация по математике на тему: Подготовка к ОГЭ 2017. Задача №26
- 2. Основная цель:Способствовать развитию логического мышления учащихся; развить
- 3. Задача №1 Три окружности, радиусы которых
- 4. Задача №1 Дано:окружность (О1; 2)окружность (О2 ;
- 5. Задача №1
- 6. Задача №1О1О2 = 5О1О3 = 12О2О3 =
- 7. Задача №2 (вар 90)Окружность с центром на
- 8. Окружность с центром на диагонали АС трапеции
- 9. Слайд 9
- 10. Задача №3 В окружности с центром
- 11. В окружности с центром О проведены две
- 12. В окружности с центром О проведены две
- 13. Задача №4 В треугольнике АВС угол
- 14. В треугольнике АВС угол В равен 120
- 15. В треугольнике АВС угол В равен 120
- 16. Задача №5 (вар 94) В равнобедренный
- 17. В равнобедренный треугольник с основанием 12 см
- 18. Е- середина АВ, АЕ = ВЕ
- 19. Задача №6 (вар 88) Отрезок ВD
- 20. Отрезок ВD является медианой равнобедренного треугольника АВС
- 21. ВD – медиана, а, значит, и высота
- 22. Задача №7 Точки М и N
- 23. Точки М и N являются серединами боковых
- 24. Точки М и N являются серединами боковых
- 25. Точки М и N являются серединами боковых
- 26. Точки М и N являются серединами боковых
Основная цель:Способствовать развитию логического мышления учащихся; развить умения учащихся применять теоретические знания при решении геометрических задач
Слайд 2Основная цель:
Способствовать развитию логического
мышления учащихся; развить умения
учащихся применять теоретические
знания при решении геометрических
задач
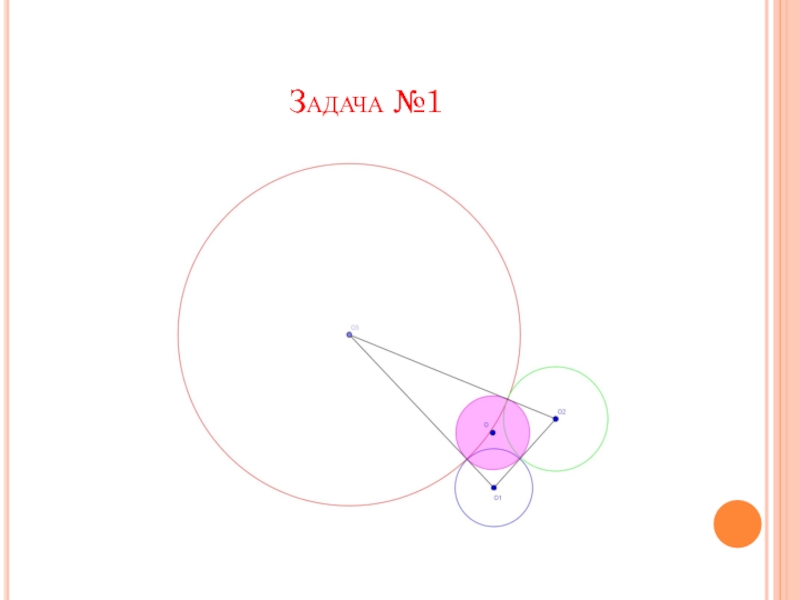
Слайд 3Задача №1
Три окружности, радиусы которых равны 2, 3 и
10 попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трех окружностей.
Слайд 4Задача №1
Дано:
окружность (О1; 2)
окружность (О2 ; 3)
окружность (О3; 10)
попарно касаются
внешним образом
окружность (О; R) вписана в треугольник О1О2О3
Найти: R
окружность (О; R) вписана в треугольник О1О2О3
Найти: R
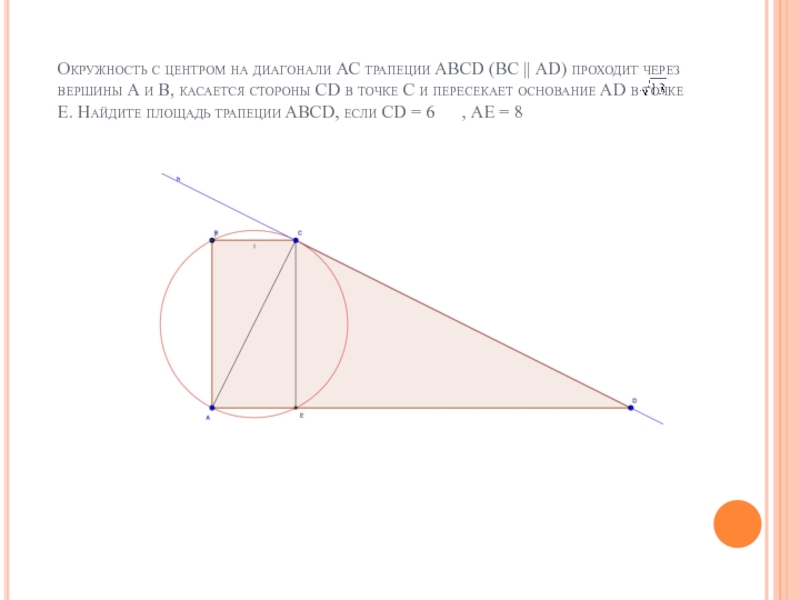
Слайд 7Задача №2 (вар 90)
Окружность с центром на диагонали АС трапеции ABCD
(ВС || AD) проходит через вершины А и В, касается стороны CD в точке С и пересекает основание AD в точке Е. Найдите площадь трапеции ABCD, если CD = 6 √13 , АЕ = 8
Слайд 8Окружность с центром на диагонали АС трапеции ABCD (ВС || AD)
проходит через вершины А и В, касается стороны CD в точке С и пересекает основание AD в точке Е. Найдите площадь трапеции ABCD, если CD = 6 , АЕ = 8
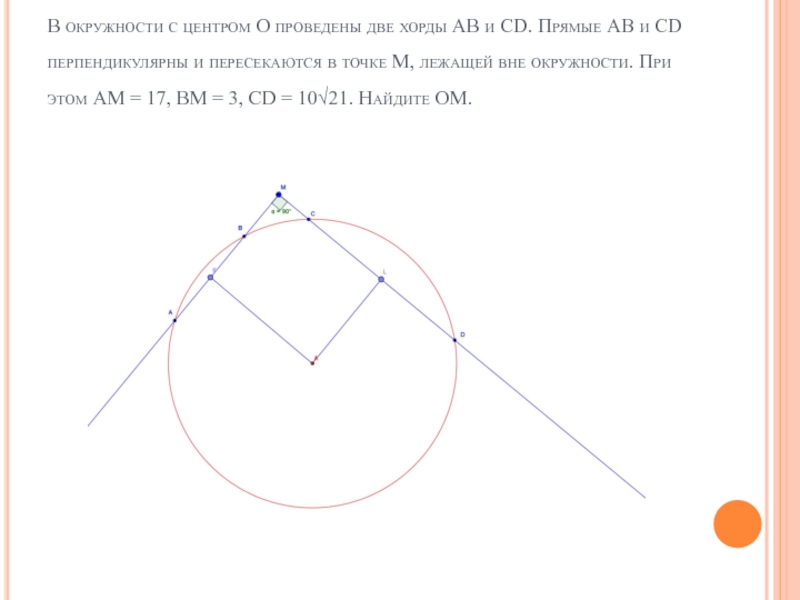
Слайд 10Задача №3
В окружности с центром О проведены две хорды
АВ и СD. Прямые АВ и СD перпендикулярны и пересекаются в точке М, лежащей вне окружности. При этом АМ = 17, ВМ = 3, СD = 10√21. Найдите ОМ.
Слайд 11В окружности с центром О проведены две хорды АВ и СD.
Прямые АВ и СD перпендикулярны и пересекаются в точке М, лежащей вне окружности. При этом АМ = 17, ВМ = 3, СD = 10√21. Найдите ОМ.
Слайд 12В окружности с центром О проведены две хорды АВ и СD.
Прямые АВ и СD перпендикулярны и пересекаются в точке М, лежащей вне окружности. При этом АМ = 17, ВМ = 3, СD = 10√21. Найдите ОМ.
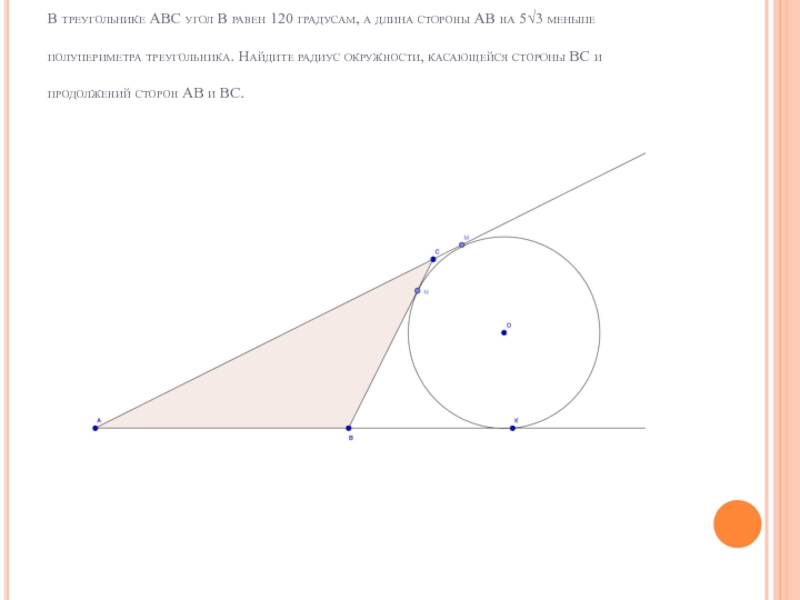
Слайд 13Задача №4
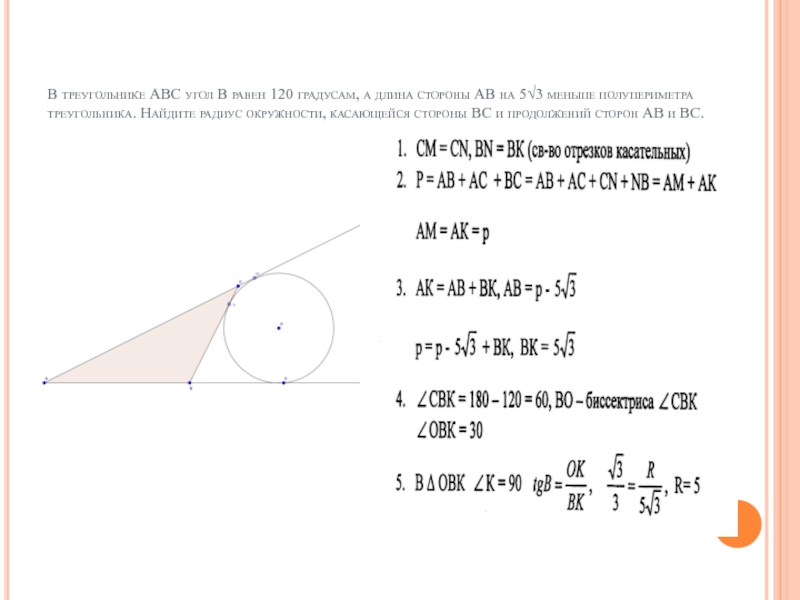
В треугольнике АВС угол В равен 120 градусам,
а длина стороны АВ на 5√3 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и ВС.
Слайд 14В треугольнике АВС угол В равен 120 градусам, а длина стороны
АВ на 5√3 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и ВС.
Слайд 15В треугольнике АВС угол В равен 120 градусам, а длина стороны
АВ на 5√3 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и ВС.
Слайд 16Задача №5 (вар 94)
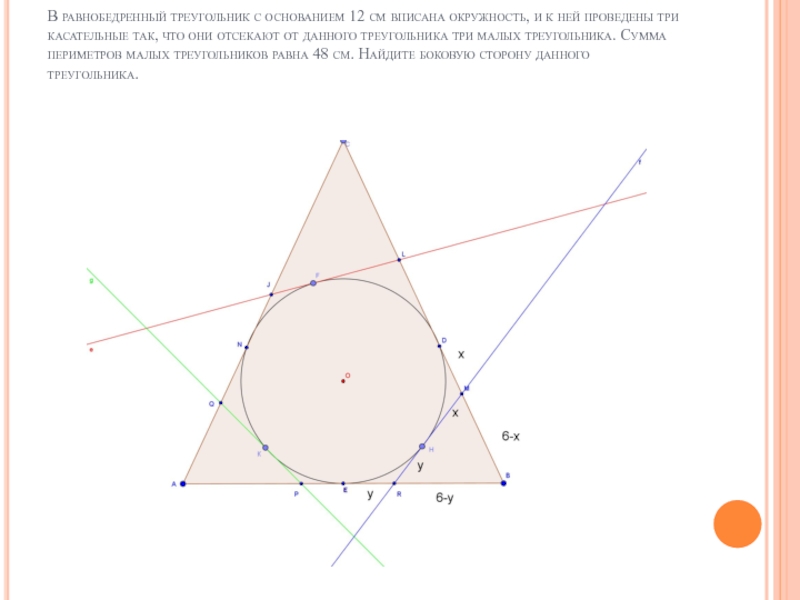
В равнобедренный треугольник с основанием 12
см вписана окружность, и к ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найдите боковую сторону данного треугольника.
Слайд 17В равнобедренный треугольник с основанием 12 см вписана окружность, и к
ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найдите боковую сторону данного треугольника.
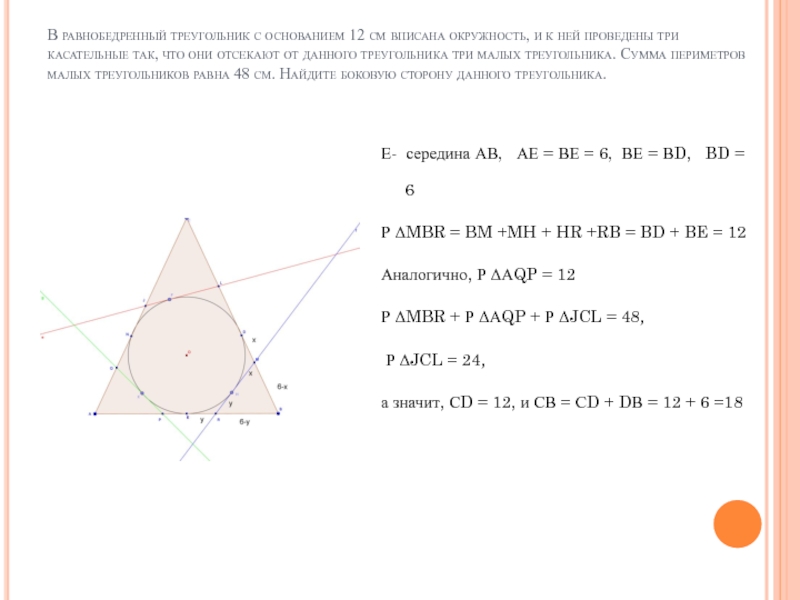
Слайд 18Е- середина АВ, АЕ = ВЕ = 6, ВЕ =
ВD, BD = 6
Р ΔMBR = BM +MH + HR +RB = BD + BE = 12
Аналогично, Р ΔАQP = 12
Р ΔMBR + Р ΔАQP + Р ΔJCL = 48,
Р ΔJCL = 24,
а значит, СD = 12, и СВ = СD + DВ = 12 + 6 =18
Р ΔMBR = BM +MH + HR +RB = BD + BE = 12
Аналогично, Р ΔАQP = 12
Р ΔMBR + Р ΔАQP + Р ΔJCL = 48,
Р ΔJCL = 24,
а значит, СD = 12, и СВ = СD + DВ = 12 + 6 =18
В равнобедренный треугольник с основанием 12 см вписана окружность, и к ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найдите боковую сторону данного треугольника.
Слайд 19Задача №6 (вар 88)
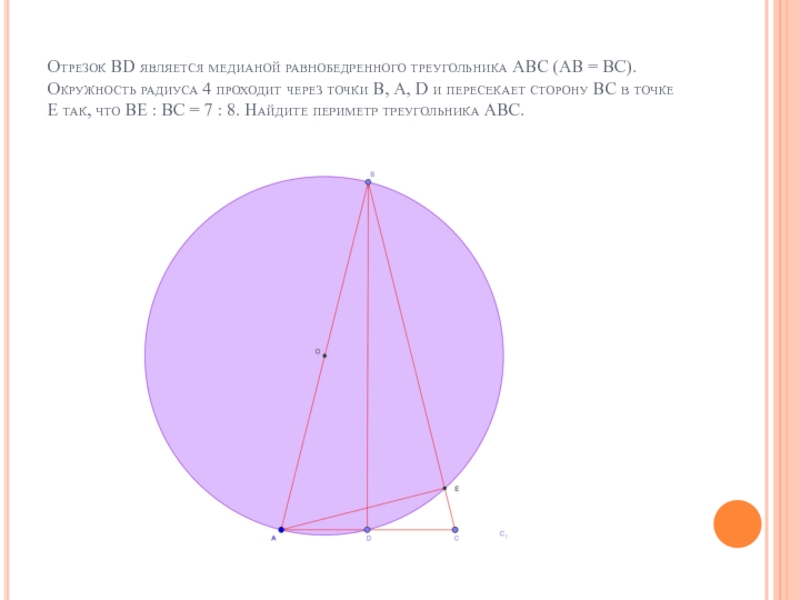
Отрезок ВD является медианой равнобедренного треугольника
АВС (АВ = ВС). Окружность радиуса 4 проходит через точки В, А, D и пересекает сторону ВС в точке Е так, что ВЕ : ВС = 7 : 8. Найдите периметр треугольника АВС.
Слайд 20Отрезок ВD является медианой равнобедренного треугольника АВС (АВ = ВС). Окружность
радиуса 4 проходит через точки В, А, D и пересекает сторону ВС в точке Е так, что ВЕ : ВС = 7 : 8. Найдите периметр треугольника АВС.
Слайд 21ВD – медиана, а, значит, и высота ΔАВС
ВDА= 90, ВDА- вписанный,
значит,
АВ – диаметр, АВ = 4 + 4 = 8
ВЕ : ВС = 7 : 8, ВЕ = 7, ЕС = 1
ВЕА- вписанный, опирается на диаметр, ВЕА= 90
В ΔАВЕ из т.Пифагора АЕ =
В ΔАСЕ по т. Пифагора АС =
Р ΔАВС = АВ + ВС + АС = 8 + 8 + 4 = 20
АВ – диаметр, АВ = 4 + 4 = 8
ВЕ : ВС = 7 : 8, ВЕ = 7, ЕС = 1
ВЕА- вписанный, опирается на диаметр, ВЕА= 90
В ΔАВЕ из т.Пифагора АЕ =
В ΔАСЕ по т. Пифагора АС =
Р ΔАВС = АВ + ВС + АС = 8 + 8 + 4 = 20
Слайд 22Задача №7
Точки М и N являются серединами боковых сторон
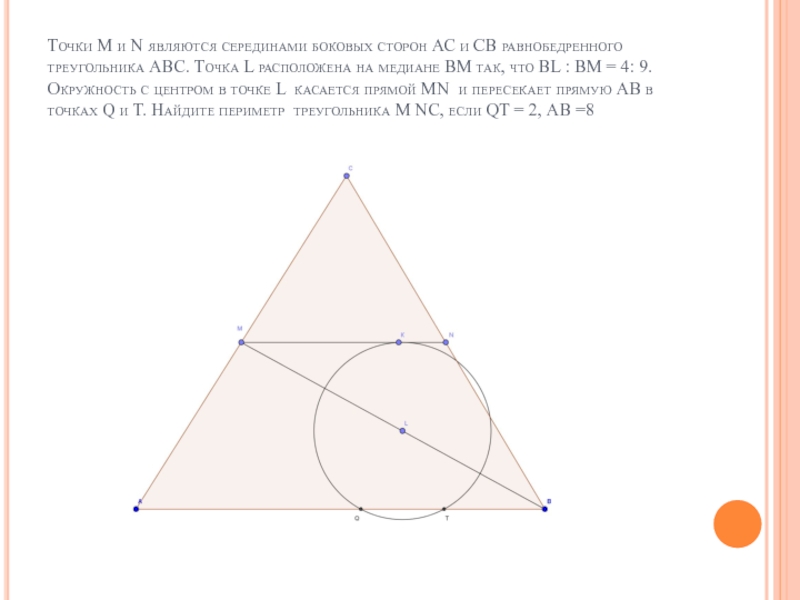
АС и СВ равнобедренного треугольника АВС. Точка L расположена на медиане ВМ так, что ВL : ВМ = 4: 9. Окружность с центром в точке L касается прямой МN и пересекает прямую АВ в точках Q и Т. Найдите периметр треугольника М NС, если QТ = 2, АВ =8
Слайд 23Точки М и N являются серединами боковых сторон АС и СВ
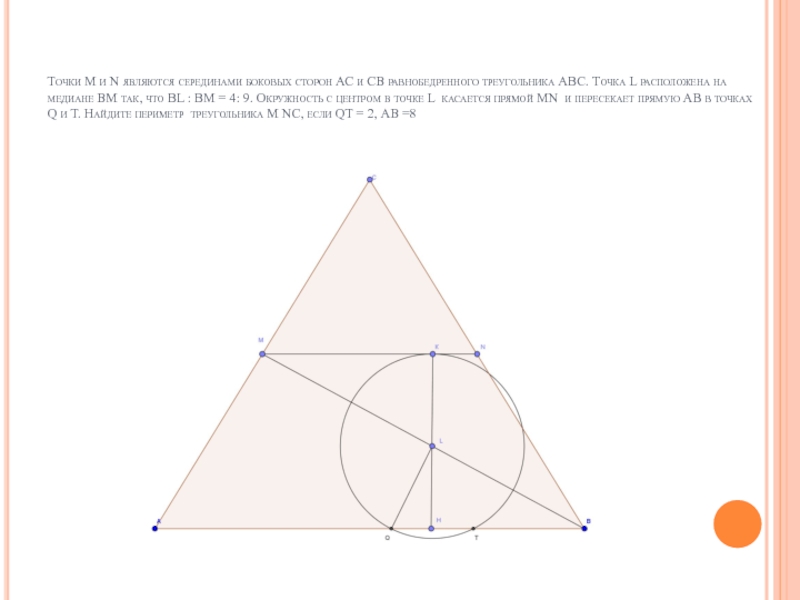
равнобедренного треугольника АВС. Точка L расположена на медиане ВМ так, что ВL : ВМ = 4: 9. Окружность с центром в точке L касается прямой МN и пересекает прямую АВ в точках Q и Т. Найдите периметр треугольника М NС, если QТ = 2, АВ =8
Слайд 24Точки М и N являются серединами боковых сторон АС и СВ
равнобедренного треугольника АВС. Точка L расположена на медиане ВМ так, что ВL : ВМ = 4: 9. Окружность с центром в точке L касается прямой МN и пересекает прямую АВ в точках Q и Т. Найдите периметр треугольника М NС, если QТ = 2, АВ =8
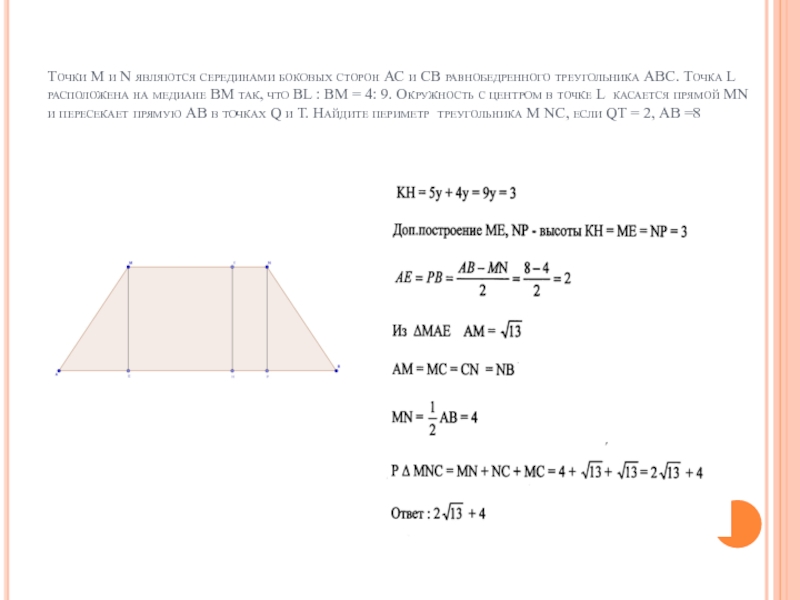
Слайд 25Точки М и N являются серединами боковых сторон АС и СВ
равнобедренного треугольника АВС. Точка L расположена на медиане ВМ так, что ВL : ВМ = 4: 9. Окружность с центром в точке L касается прямой МN и пересекает прямую АВ в точках Q и Т. Найдите периметр треугольника М NС, если QТ = 2, АВ =8
Слайд 26Точки М и N являются серединами боковых сторон АС и СВ
равнобедренного треугольника АВС. Точка L расположена на медиане ВМ так, что ВL : ВМ = 4: 9. Окружность с центром в точке L касается прямой МN и пересекает прямую АВ в точках Q и Т. Найдите периметр треугольника М NС, если QТ = 2, АВ =8