- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему подготовка к ЕГЭ
Содержание
- 1. Презентация по математике на тему подготовка к ЕГЭ
- 2. Решение.Значение производной в точке касания равно угловому
- 3. 2. На р исунке изображён график функции
- 4. Решение.По определению первообразной на интервале (−2; 4)
- 5. 3. Материальная точка движется прямолинейно по закону
- 6. 4.На рисунке изображён график некоторой функции
- 7. Решение.Найдем формулу, задающую функцию
- 8. 7.На рисунке изображен график производной функции f(x),
- 9. Решение.Значение производной в точке касания равно
- 10. 9.На рисунке изображен график функции , определенной
- 11. Решение.Производная функции положительна на тех интервалах, на
- 12. 10.На рисунке изображен график
- 13. Решение.Значение производной в точке касания равно угловому
- 14. 12.На рисунке изображен график
- 15. Решение. Заданная функция имеет максимумы в
- 16. http://mathege.ru/or/ege/Main − Материалы открытого банка заданий по математике 2015 года Используемые материалы
Решение.Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения : Ответ: −0,5.. 1.Прямая
Слайд 2Решение.Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения :
Ответ: −0,5.
Ответ: −0,5.
. 1.Прямая параллельна касательной к графику функции .
Найдите абсциссу точки касания.
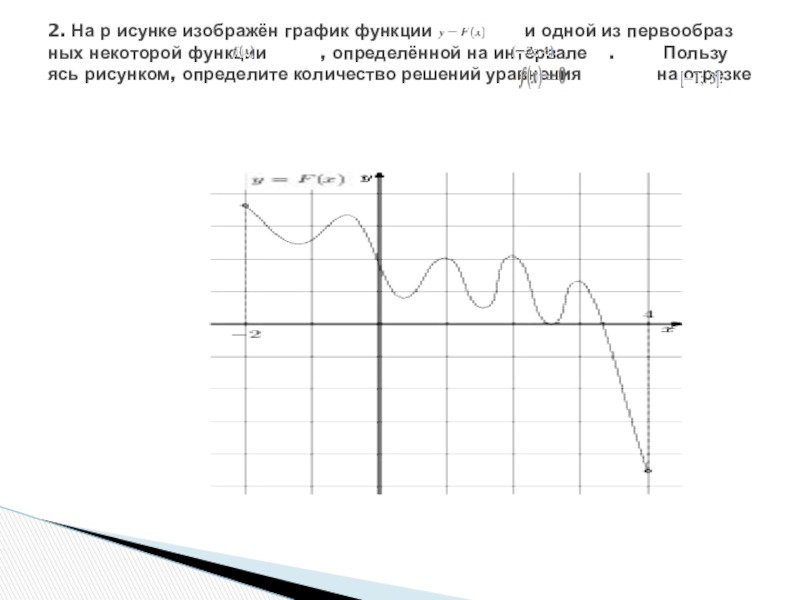
Слайд 32. На р исунке изображён график функции
и одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке
Слайд 4Решение.
По определению первообразной на интервале (−2; 4) справедливо равенство
Следовательно,
решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,2; −0,4; 0,4; 1; 1,6; 2; 2,6; 3. Из них на отрезке [−1; 3] лежат 7 точек. Таким образом, на отрезке [−1; 3] уравнение f(x) = 0 имеет 7 решений.
Ответ: 7.
Ответ: 7.
№2
Слайд 53. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Решение.
Найдем закон изменения скорости: м/с. Чтобы найти, в какой момент времени скорость была равна 2 м/с, решим уравнение:
. Ответ: 7.
Решение.
Найдем закон изменения скорости: м/с. Чтобы найти, в какой момент времени скорость была равна 2 м/с, решим уравнение:
. Ответ: 7.
Слайд 64.
На рисунке изображён график некоторой функции .
Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Слайд 7Решение.
Найдем формулу, задающую функцию график которой изображён на
рисунке.
Следовательно, график функции получен сдвигом графика функции на единиц вправо вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции и отрезком оси абсцисс. Имеем:
Ответ: 2,7.
Следовательно, график функции получен сдвигом графика функции на единиц вправо вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции и отрезком оси абсцисс. Имеем:
Ответ: 2,7.
№4
Слайд 8
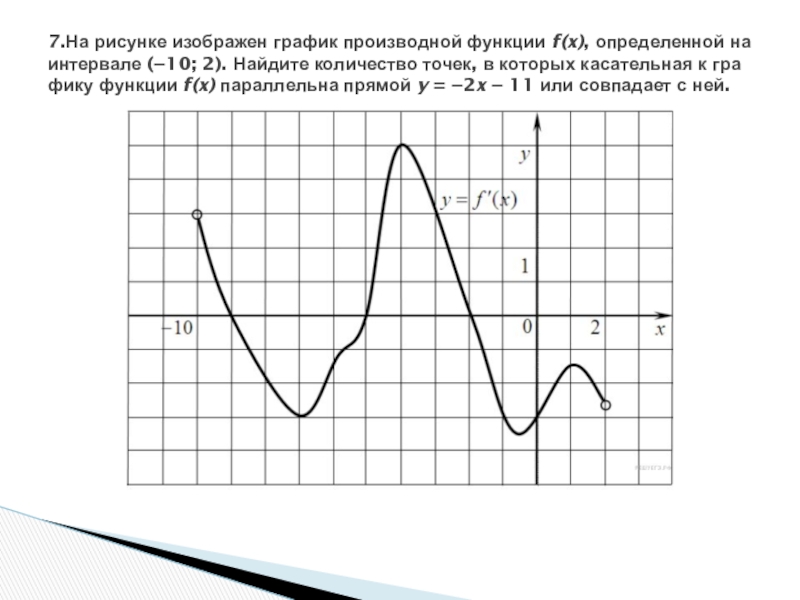
7.На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2).
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
Слайд 9
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой y = −2x − 11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых y'(x0) = −2, это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.
Ответ: 5.
Ответ: 5.
№7
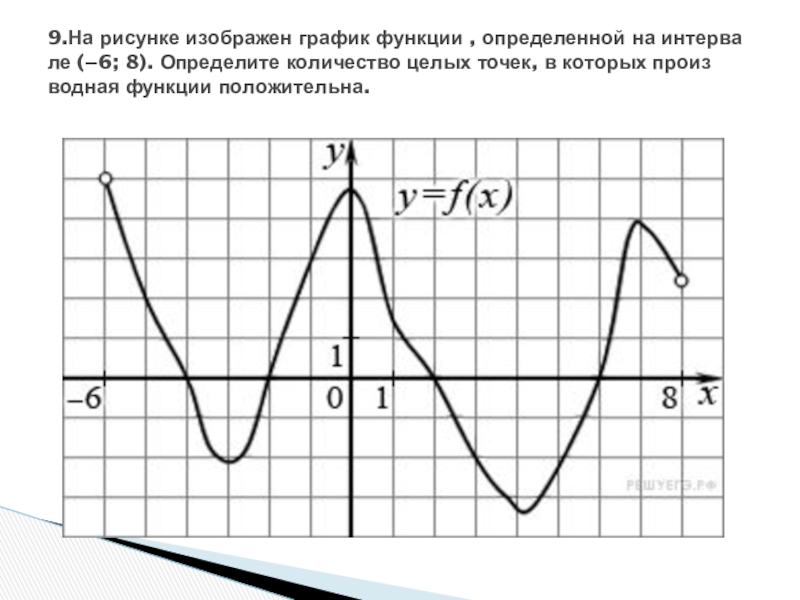
Слайд 109.На рисунке изображен график функции , определенной на интервале (−6; 8).
Определите количество целых точек, в которых производная функции положительна.
Слайд 11Решение.
Производная функции положительна на тех интервалах, на которых функция возрастает, т. е.
на интервалах (−3; 0) и (4,2; 7). В них содержатся целые точки −2, −1, 5 и 6, всего их 4.
Ответ: 4.
Ответ: 4.
№9
Слайд 12
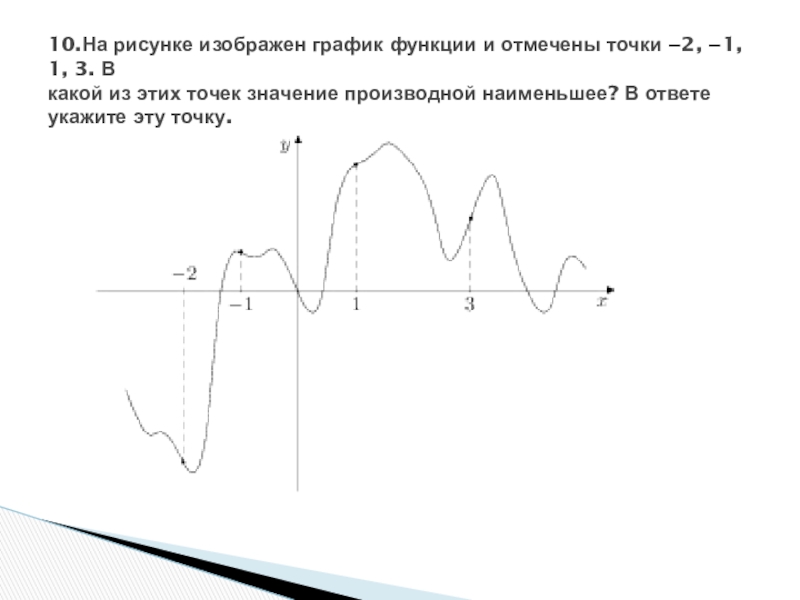
10.На рисунке изображен график функции и отмечены точки −2, −1, 1,
3. В
какой из этих точек значение производной наименьшее? В ответе
укажите эту точку.
Слайд 13Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в
свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках −2 и −1. Модуль тангенса угла наклона касательной явно больше в точке −2, поэтому тангенс в этой точке наименьший. Ответ: −2.
№10
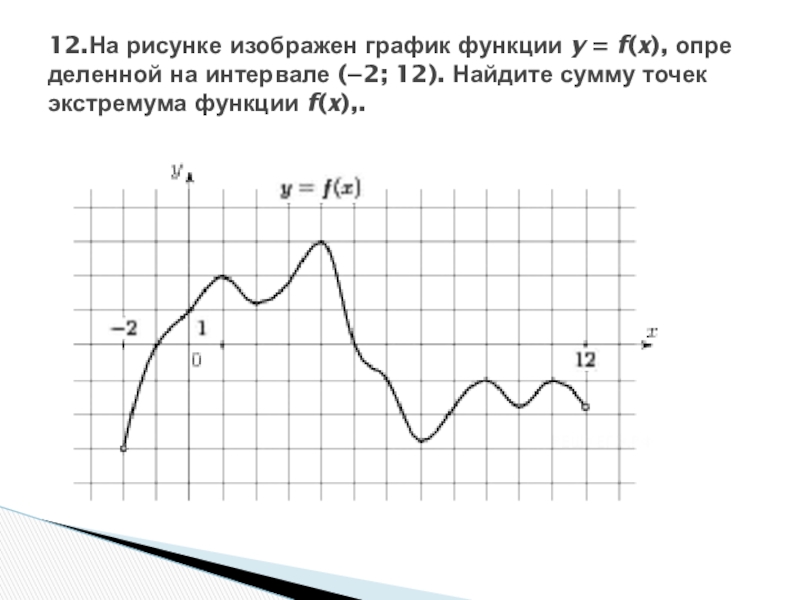
Слайд 14 12.На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите
сумму точек экстремума функции f(x),.
Слайд 15
Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и
минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
Ответ: 44.
Ответ: 44.
№12
Слайд 16http://mathege.ru/or/ege/Main − Материалы открытого банка заданий по математике 2015 года
Используемые
материалы