- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Подготовка к ЕГЭ. Возрастание и убывание функции (11 класс)
Содержание
- 1. Презентация по математике на тему Подготовка к ЕГЭ. Возрастание и убывание функции (11 класс)
- 2. Повторение материалаПонятия возрастающей и убывающей функций.Понятие монотонности функции.
- 3. Возрастающая функцияФункция f(х) называется возрастающей на некотором
- 4. Убывающая функцияФункция f(х) называется убывающей на некотором
- 5. Возрастающие и убывающие функции называются монотонными функциями
- 6. Пример №1По графику функции y=f(x) ответьте на
- 7. Пример №2По графику функции y=f´(x) ответьте на
- 8. ЦелиНайти связь между производной и свойством монотонности
- 9. Тема: «Возрастание и убывание функции»
- 10. Слайд 10
- 11. Если f/(x) > 0 на некотором
- 12. Непрерывная функция y=f(x) задана на [-10;11]. На
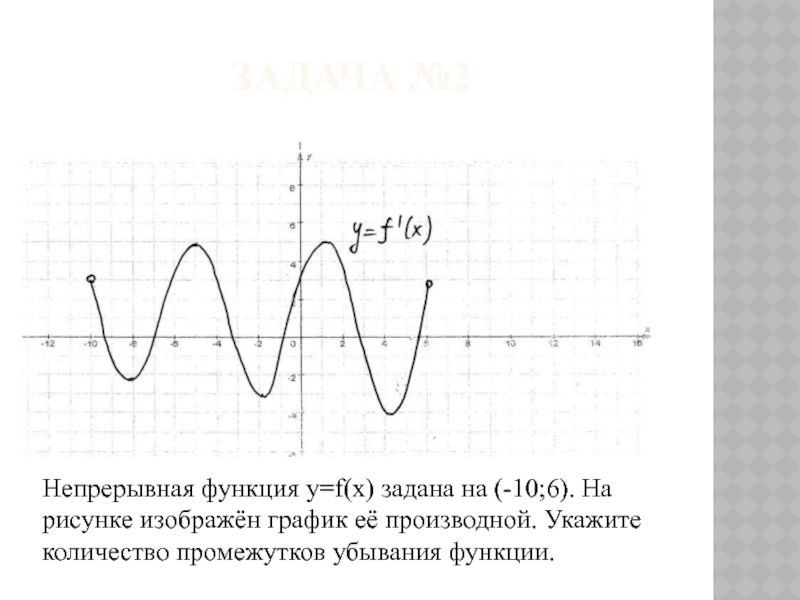
- 13. Непрерывная функция y=f(x) задана на (-10;6). На
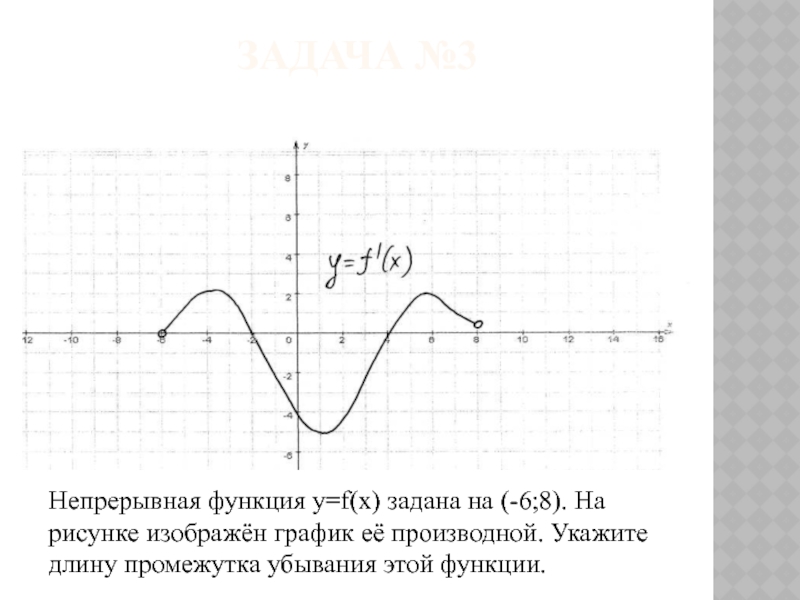
- 14. Непрерывная функция y=f(x) задана на (-6;8). На
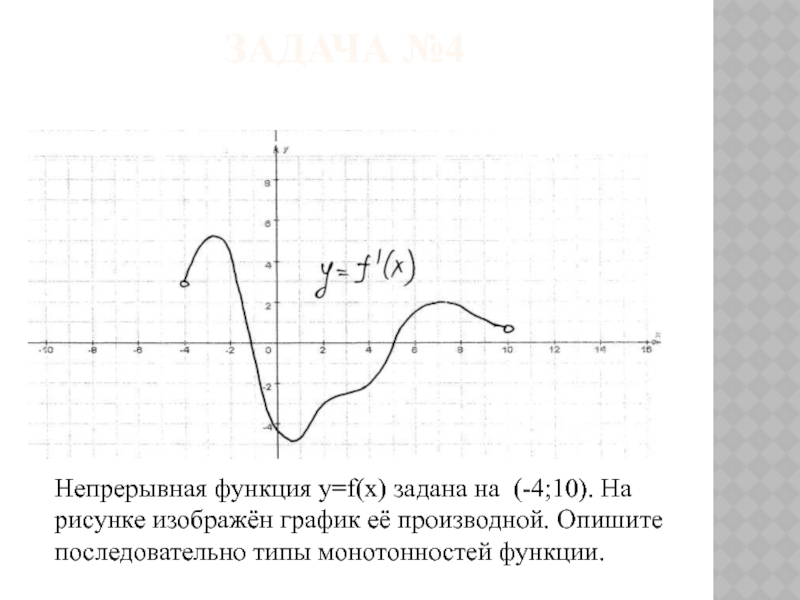
- 15. Непрерывная функция y=f(x) задана на (-4;10). На
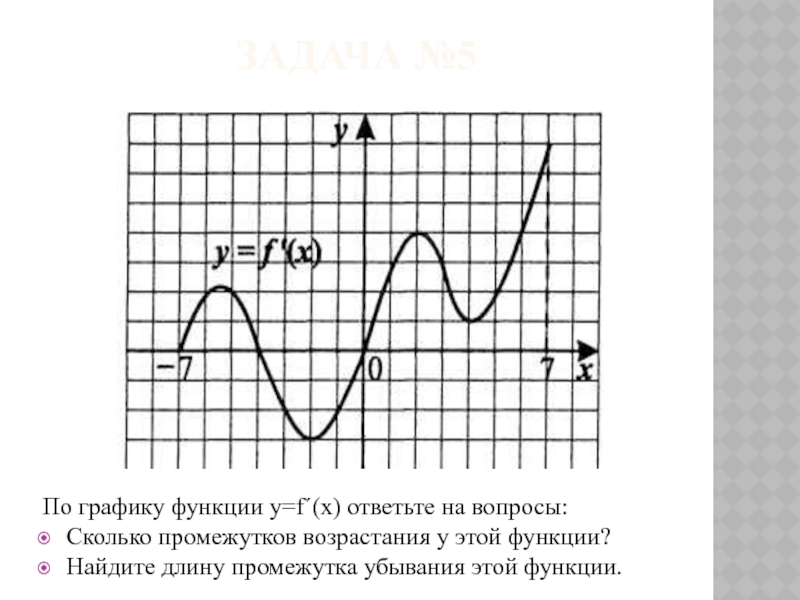
- 16. По графику функции y=f´(x) ответьте на вопросы:Сколько
- 17. АлгоритмУказать область определения функции.Найти производную функции.Определить промежутки,
- 18. Образец решения по алгоритму f(х) = х4 -
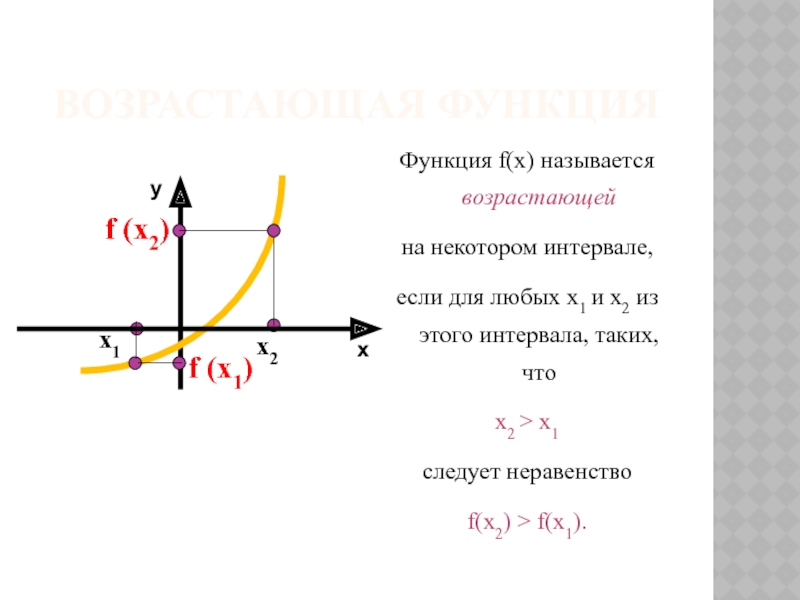
- 19. На рисунке изображён график дифференцируемой функции y
- 20. Ответ: 3 Ответ: 14
- 21. Слайд 21
- 22. Слайд 22
- 23. Спасибо за внимание
Повторение материалаПонятия возрастающей и убывающей функций.Понятие монотонности функции.
Слайд 1Подготовка к ЕГЭ
«Возрастание и убывание функции»
Санкт-Петербург
Учитель математики
Пачина Ирина Сергеевна
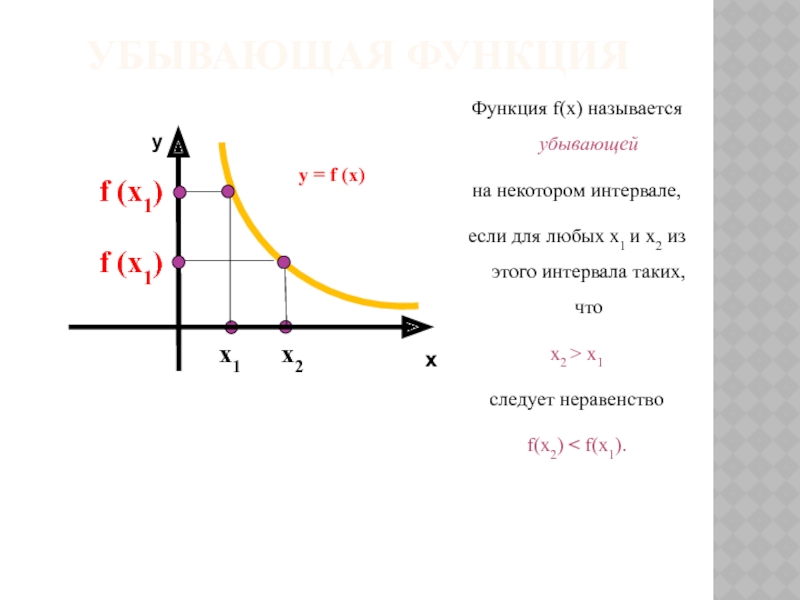
Слайд 3Возрастающая функция
Функция f(х) называется возрастающей
на некотором интервале,
если для любых
х1 и х2 из этого интервала, таких, что
х2 > х1
следует неравенство
f(х2) > f(х1).
х2 > х1
следует неравенство
f(х2) > f(х1).
х
х1
х2
у
f (х1)
f (х2)
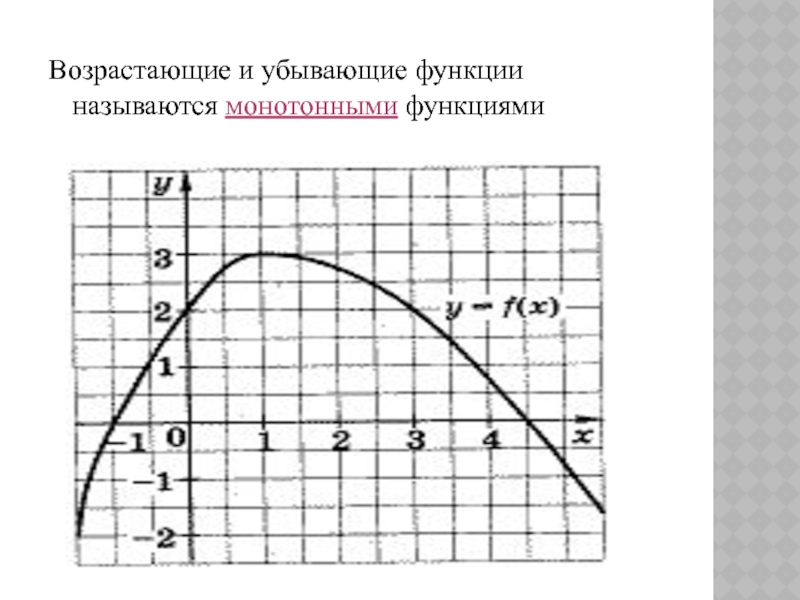
Слайд 4Убывающая функция
Функция f(х) называется убывающей
на некотором интервале,
если для любых
х1 и х2 из этого интервала таких, что
х2 > х1
следует неравенство
f(х2) < f(х1).
х2 > х1
следует неравенство
f(х2) < f(х1).
х1
х2
f (х1)
f (х1)
у = f (х)
у
х
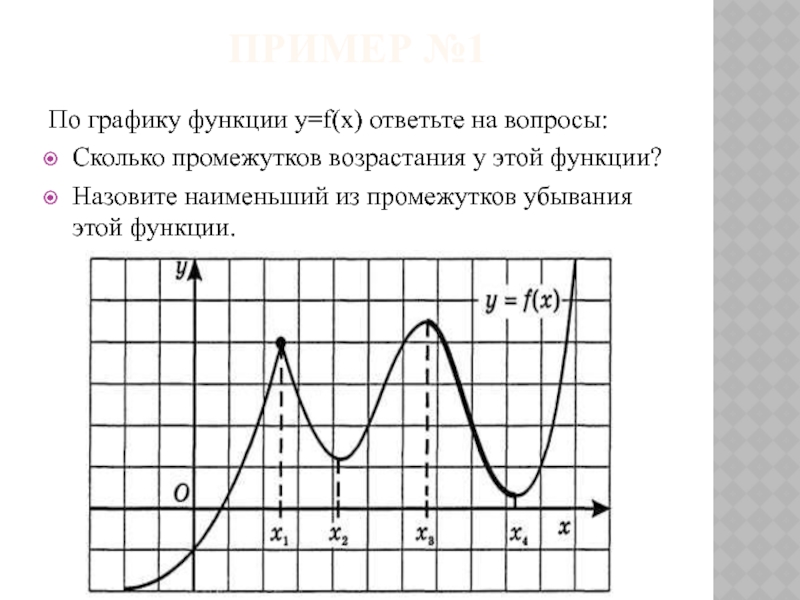
Слайд 6Пример №1
По графику функции y=f(x) ответьте на вопросы:
Сколько промежутков возрастания у
этой функции?
Назовите наименьший из промежутков убывания этой функции.
Назовите наименьший из промежутков убывания этой функции.
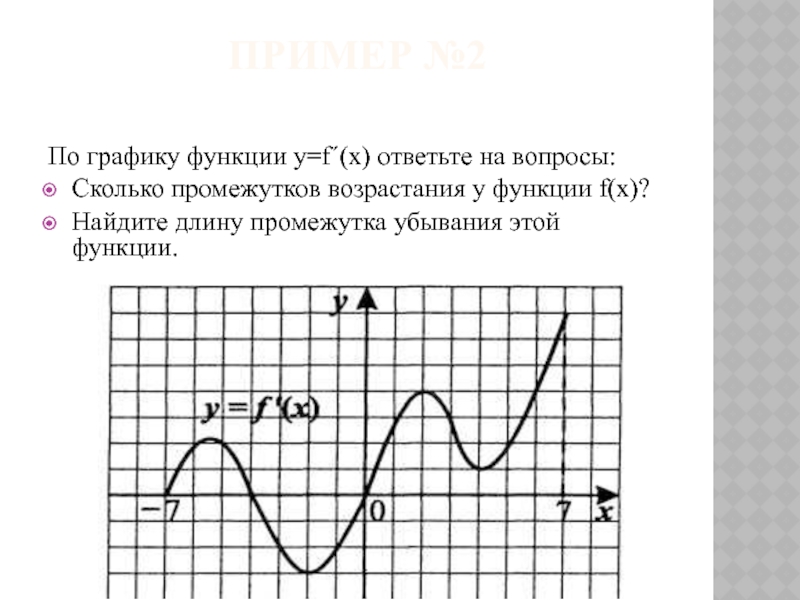
Слайд 7Пример №2
По графику функции y=f´(x) ответьте на вопросы:
Сколько промежутков возрастания у
функции f(x)?
Найдите длину промежутка убывания этой функции.
Найдите длину промежутка убывания этой функции.
Слайд 8Цели
Найти связь между производной и свойством монотонности функции.
Создать алгоритм поиска промежутков
монотонности функции с помощью производной.
Слайд 11 Если f/(x) > 0 на некотором интервале, то функция возрастает
на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале.
Слайд 12Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её
производной. Укажите количество промежутков возрастания функции.
Задача №1
![Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.Задача](/img/thumbs/56d4ac9ade2312c616dffd5509e35173-800x.jpg "Презентация по математике на тему Подготовка к ЕГЭ. Возрастание и убывание функции (11 класс) Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её")
Слайд 13Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её
производной. Укажите количество промежутков убывания функции.
Задача №2
Слайд 14Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её
производной. Укажите длину промежутка убывания этой функции.
Задача №3
Слайд 15Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её
производной. Опишите последовательно типы монотонностей функции.
Задача №4
Слайд 16По графику функции y=f´(x) ответьте на вопросы:
Сколько промежутков возрастания у этой
функции?
Найдите длину промежутка убывания этой функции.
Найдите длину промежутка убывания этой функции.
Задача №5
Слайд 17Алгоритм
Указать область определения функции.
Найти производную функции.
Определить промежутки, в которых f/(x) >
0 и f/(x) < 0.
Сделать выводы о монотонности
функции.
Сделать выводы о монотонности
функции.
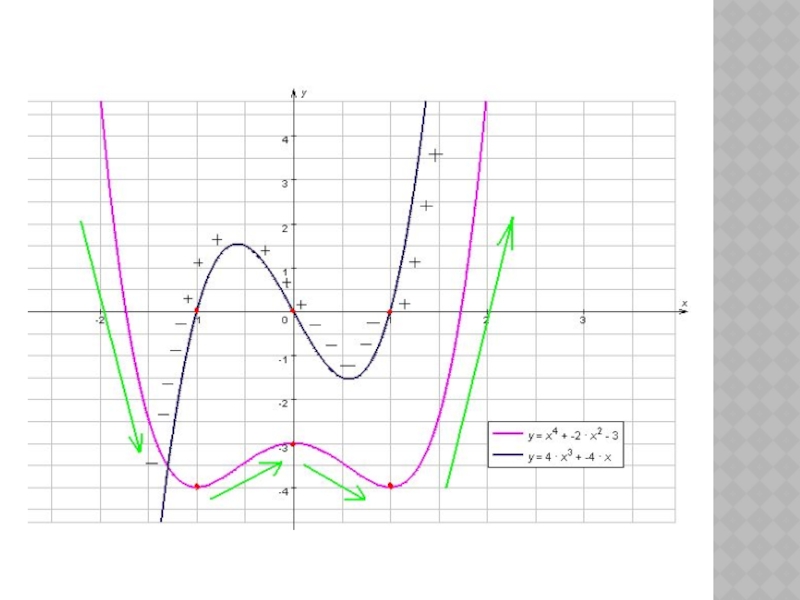
Слайд 18Образец решения по алгоритму
f(х) = х4 - 2х2 ,
D(f) = R
f/(x)
= 4х3 - 4х,
f/(x)>0, если 4х3 - 4х >0, х3 - х >0, х(х-1)(х+1)>0
f/(x)>0, если 4х3 - 4х >0, х3 - х >0, х(х-1)(х+1)>0
f/(x): - + - +
f(х):
-1 0 1 х
4. Функция убывает на промежутках (-∞;-1)] и [(0; 1)] .
Функция возрастает на промежутках [(-1; 0)] и [(1; + ∞)]
Слайд 19На рисунке изображён график дифференцируемой функции y = f(x). На оси
абсцисс отмечены девять точек: x1 , x2 , ..., x9. Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
