- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Функции, их свойства и графики в заданиях ОГЭ.(2 часть) (9 класс)
Содержание
- 1. Презентация по математике на тему Функции, их свойства и графики в заданиях ОГЭ.(2 часть) (9 класс)
- 2. Для того, чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать Р.Декарт
- 3. № 1. Повторение.Линейные функции.y = kх + b
- 4. № 2. Повторение.Функции прямой пропорциональности.у = kx
- 5. № 3. Повторение.Функции обратной пропорциональности.у = k/x
- 6. № 4. Повторение.Квадратичные функции.у = ах2 + bx +c
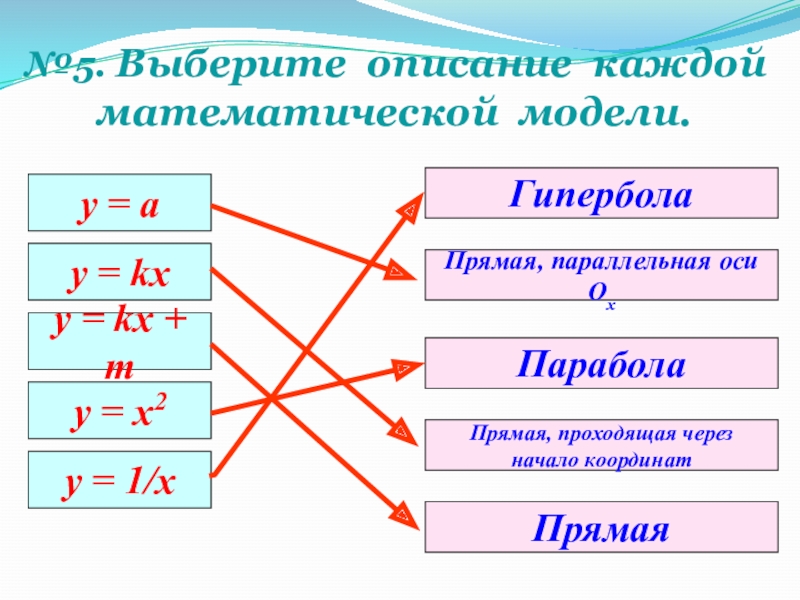
- 7. у = а y = kxy =
- 8. №6. Найдите соответствия:Какой график является графикомфункции прямойпропорциональности?
- 9. №7. Повторение.
- 10. Слайд 10
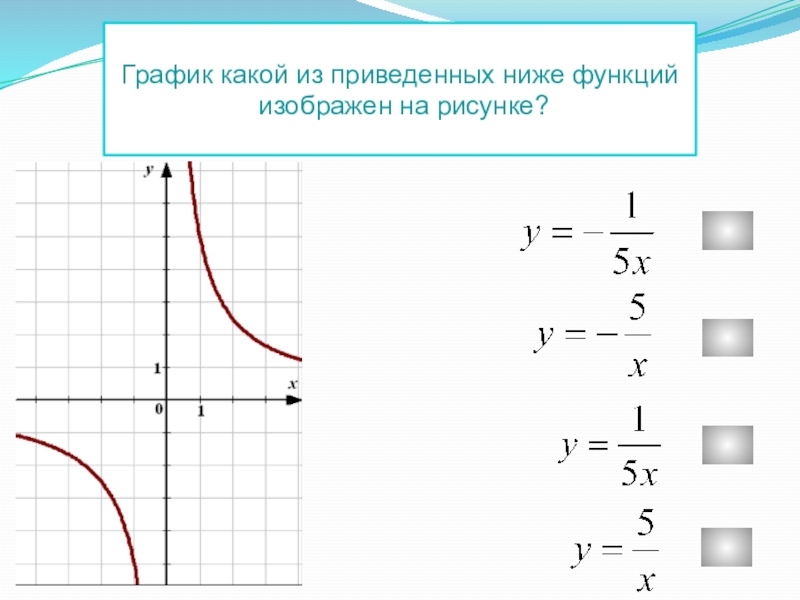
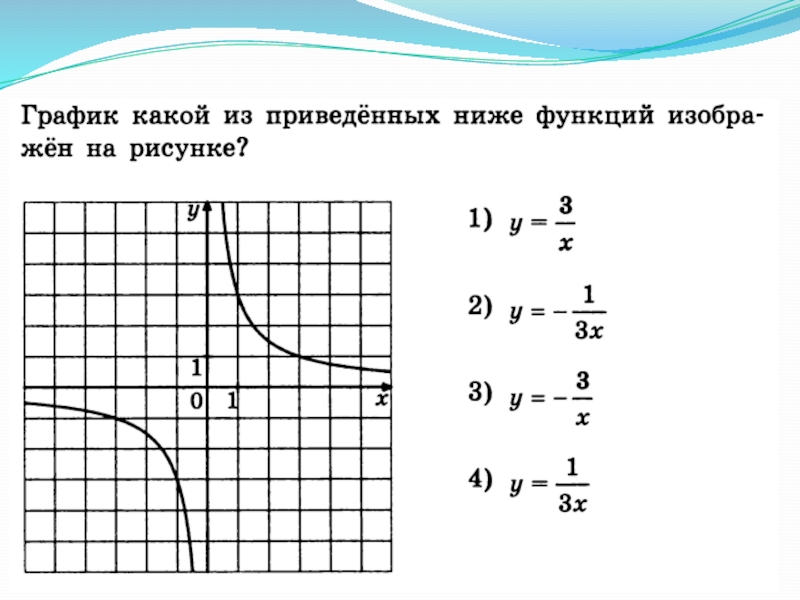
- 11. График какой из приведенных ниже функций изображен на рисунке?
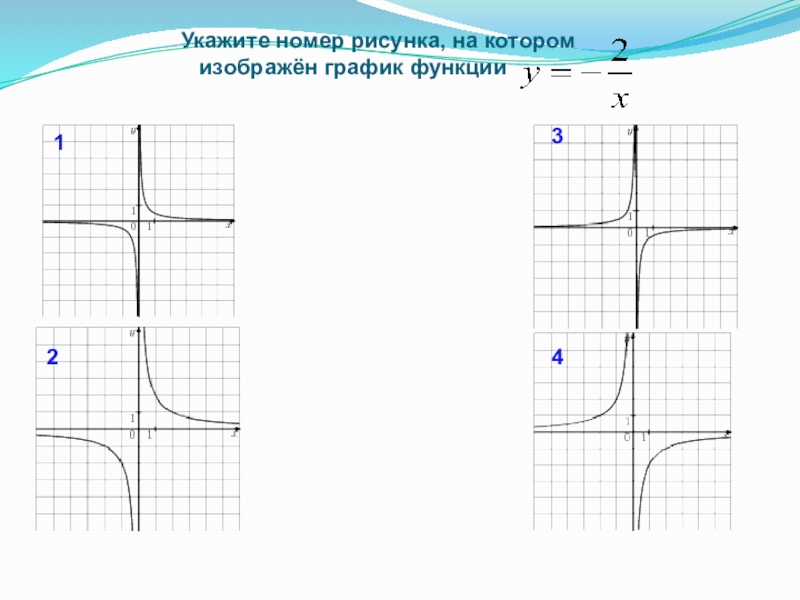
- 12. Укажите номер рисунка, на котором
- 13. Слайд 13
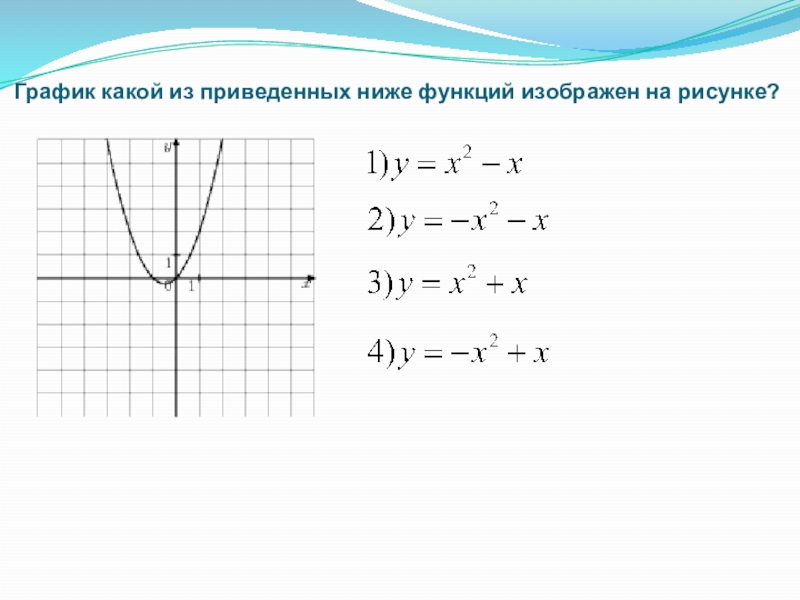
- 14. График какой из приведенных ниже функций изображен на рисунке?
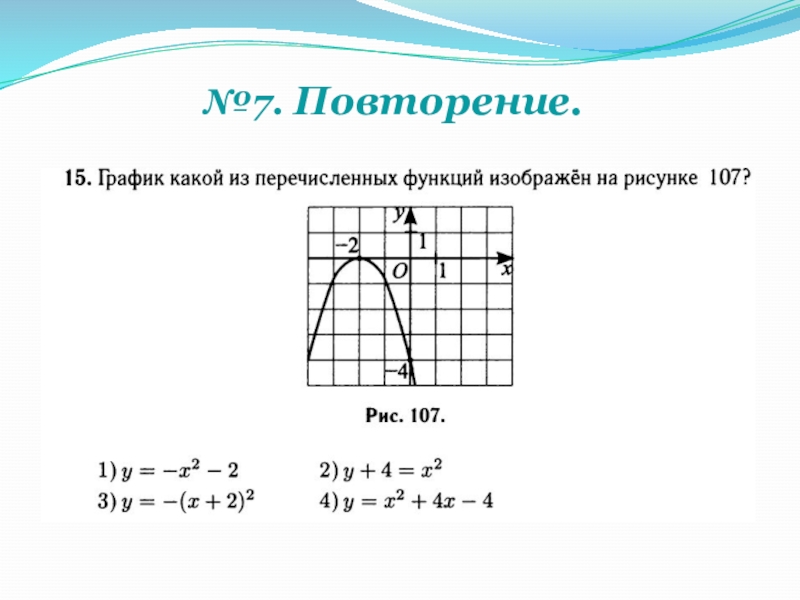
- 15. График какой из приведенных ниже функций
- 16. Найти значения a и b по
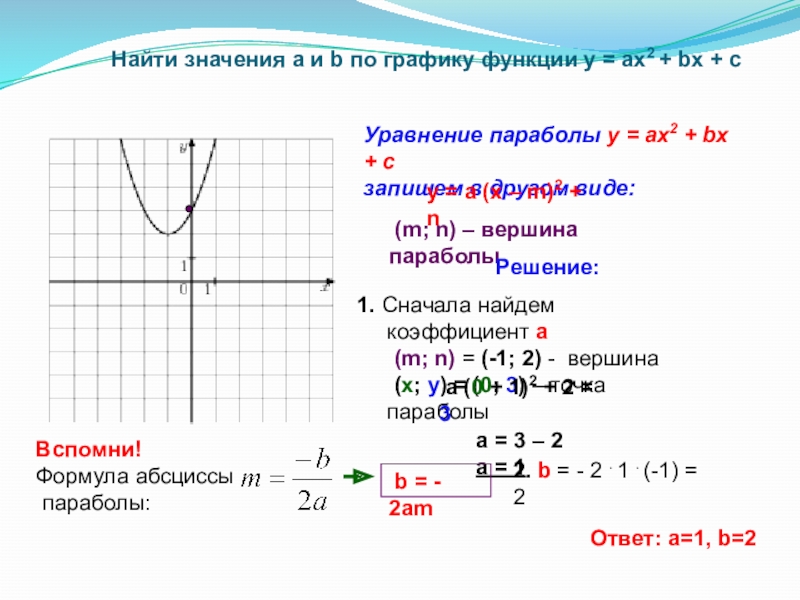
- 17. Найти значения a и b по
- 18. Найти значение c по графику функции
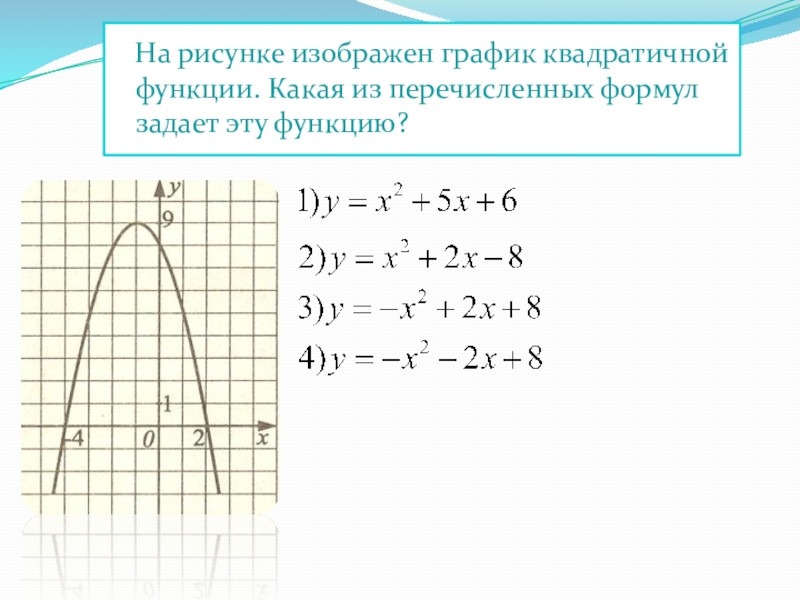
- 19. На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?
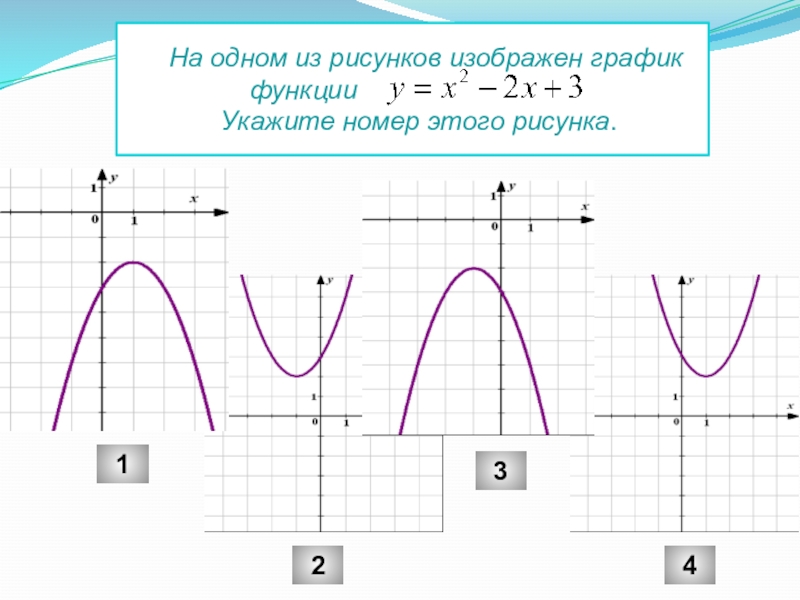
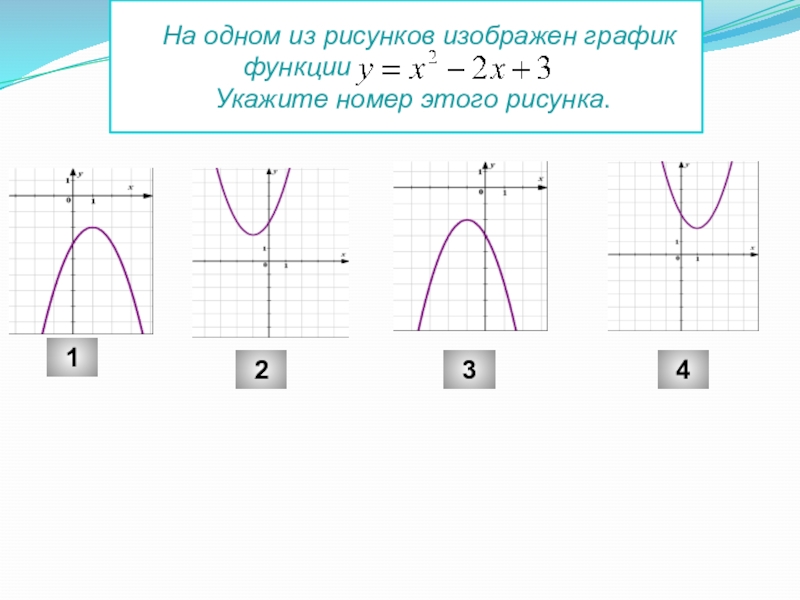
- 20. На одном из рисунков
- 21. На одном из рисунков
- 22. Слайд 22
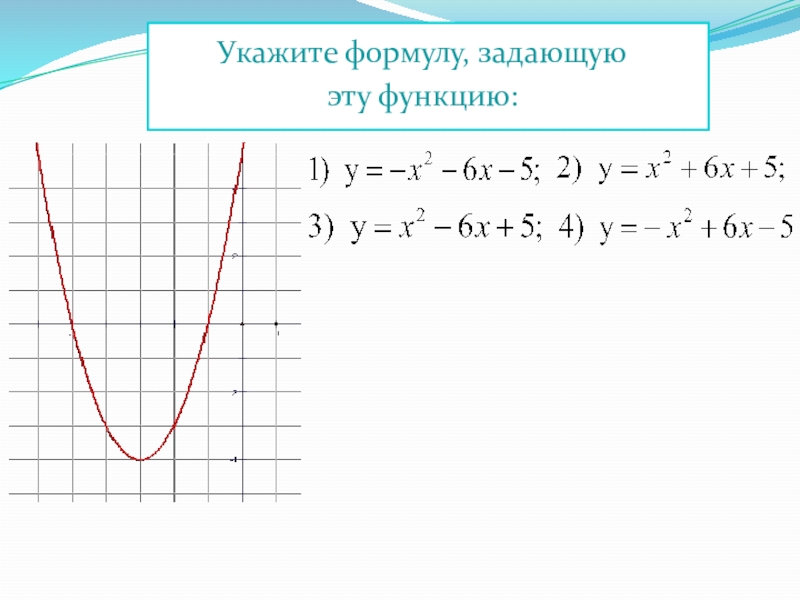
- 23. Укажите формулу, задающую эту функцию:
- 24. Спасибоза внимание!
Слайд 7у = а
y = kx
y = kx + m
y =
y = 1/x
Прямая, параллельная оси Ох
Парабола
Гипербола
Прямая, проходящая через
начало координат
Прямая
№5. Выберите описание каждой
математической модели.
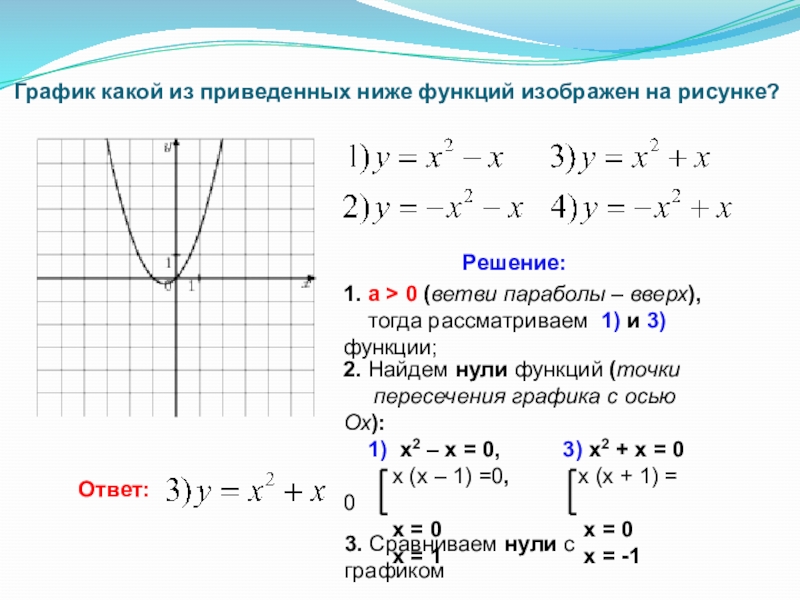
Слайд 15 График какой из приведенных ниже функций изображен на рисунке?
Решение:
1. a
тогда рассматриваем 1) и 3) функции;
2. Найдем нули функций (точки
пересечения графика с осью Ох):
1) х2 – х = 0, 3) х2 + х = 0
х (х – 1) =0, х (х + 1) = 0
х = 0 х = 0
х = 1 х = -1
3. Сравниваем нули с графиком
Ответ:
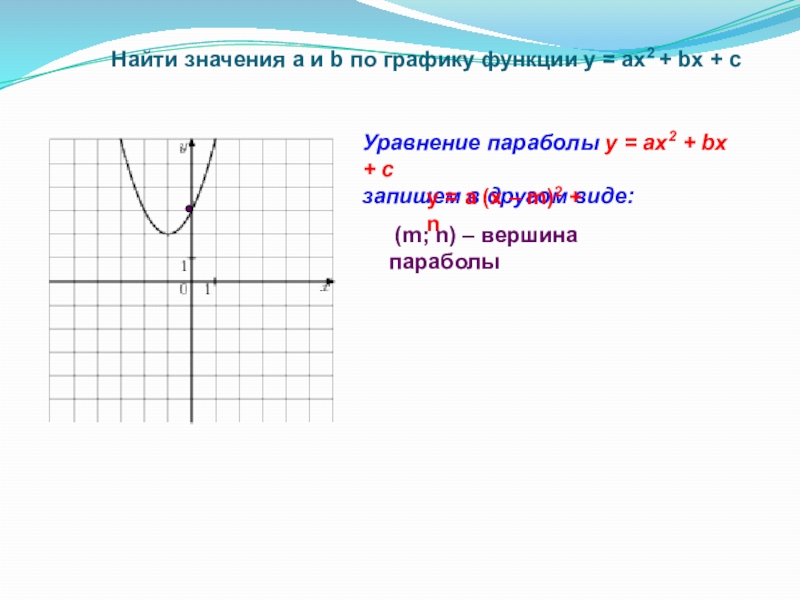
Слайд 16 Найти значения a и b по графику функции у =
Уравнение параболы у = ax2 + bx + c
запишем в другом виде:
y = a (x – m)2 + n
(m; n) – вершина параболы
Слайд 17 Найти значения a и b по графику функции у =
Уравнение параболы у = ax2 + bx + c
запишем в другом виде:
y = a (x – m)2 + n
(m; n) – вершина параболы
Решение:
1. Сначала найдем коэффициент а
(m; n) = (-1; 2) - вершина
(х; у) = (0; 3) – точка параболы
Вспомни!
Формула абсциссы
параболы:
a (0 + 1)2 + 2 = 3
а = 3 – 2
а = 1
Ответ: a=1, b=2
b = - 2am
2. b = - 2 . 1 . (-1) = 2
Слайд 18 Найти значение c по графику функции у = ах2 +
Ответ: с = 3
(0; c) – точка пересечения
параболы с осью Оу
Примечание: не всегда возможно назвать
ординату точки пересечения с Оу.
Поиск значения с:
1) коэффициент а
2) коэффициент b
(смотри задачи выше)
3) с находим из уравнения
у = ах2 + bx + c