- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Диофантовы уравнения (9 класс)
Содержание
- 1. Презентация по математике на тему Диофантовы уравнения (9 класс)
- 2. СПИСОК УРОКОВУрок 1. Понятие диофантовых уравнений. Теоремы.Урок
- 3. УРОК 1Понятие диофантовых уравнений. Теоремы.Начать
- 4. УРОК 1Тема: Понятие диофантовых уравнений. Теоремы.Цель: изучить
- 5. УРОК 1Попытаемся решить следующую задачу:Покупка свитера.Вы должны
- 6. УРОК 1Попытаемся решить следующую задачу:Покупка свитера.Вы должны
- 7. УРОК 1 Итак, обозначим понятие диофантового уравнения. Диофантовы уравнения
- 8. УРОК 1Задание 1. Определите, является ли диофантовым уравнение. Аргументировать свой ответ.71x-9y=15x+8y=2,6x2+y2=95,1x+4,6y2=86y+13x-2z=8-9x+17z=0Примечание: диофантовы уравнения имеют целые коэффициентыДалее
- 9. УРОК 1Термин диофантовы уравнения берет свое начало
- 10. УРОК 1До нашего времени, дошла примерно половина
- 11. УРОК 1Теперь, выясним, всегда ли возможно решить
- 12. УРОК 1Задание 2. Используя вышеприведенные теоремы определите, имеют ли решения следующие диофантовы уравнения:6x+12y=136x+7y=1418y+9z=827x+4y=56x+2y=1Далее
- 13. УРОК 1 ЗАВЕРШЕНСледующий урокВернуться к началу урокаВыбрать урок
- 14. УРОК 2Методы решения диофантовых уравнений. Метод спуска или рассеивания.Начать
- 15. УРОК 2Тема: Методы решения диофантовых уравнений. Метод
- 16. УРОК 2 В теории чисел созданы специальные методы
- 17. УРОК 2 Наиболее сложной задачей диофантового анализа является
- 18. УРОК 2 На этом уроке мы научимся решать
- 19. УРОК 2Решение Выразим x через у: Так
- 20. УРОК 2 Задание 3. Самостоятельно закончите решение
- 21. УРОК 2 Таким образом, используя формулы и рассуждения
- 22. УРОК 2 ЗАВЕРШЕНСледующий урокВернуться к началу урокаВыбрать урок
- 23. УРОК 3Решение диофантовых уравнений, как квадратных. Использование тождественные преобразований.Начать
- 24. УРОК 3Тема: Решение диофантовых уравнений, как квадратных.
- 25. УРОК 3 Метод спуска бесспорно удобен и наиболее
- 26. УРОК 3РешениеНеобходимо путем тождественных преобразований в левой
- 27. УРОК 3Задание 5. Самостоятельно составьте оставшиеся 6
- 28. УРОК 3 В отдельных случаях после тождественных преобразований
- 29. УРОК 3Рассмотрим уравнение, как квадратное относительно x3x2+3xy+3y2-x-8y=03x2+3xy-x+3y2-8y=03x2+(3y-1)x+3y2-8y=0D=(3y-1)2-4*3*(3y2-8y)=9y2-6y+1-36y2+96y=-27y2+90y+1Данное
- 30. УРОК 3Задание 6. Самостоятельно найдите все решения уравнений в множестве целых чиселxy+3x-5y=-3x2-9y2=19x3+y3=35Примечание: используете формулы сокращенного умноженияДалее
- 31. УРОК 3 ЗАВЕРШЕНСледующий урокВернуться к началу урокаВыбрать урок
- 32. УРОК 4Метод от противного. Метод остатков. Метод параметризации.Начать
- 33. УРОК 4Тема: Метод от противного. Метод остатков.
- 34. УРОК 4РешениеПреобразуем выражение, используя формулу сокращенного умножения:x2-y2=1990(x-y)(x+y)=1990Пусть
- 35. УРОК 4 При решении диофантовых уравнений полезно сравнивать
- 36. УРОК 4x3-x=3y2+1x(x2-1)=3y2+1(x-1)x(x+1)=3y2+1Левая часть уравнения как произведение трех
- 37. УРОК 4 При доказательстве бесконечности множества целых решений
- 38. УРОК 4Доказать, что уравнение x2+y2=z2 имеет бесконечное
- 39. УРОК 4Задание 8. Самостоятельно определите имеют ли
- 40. УРОК 4 ЗАВЕРШЕНСледующий урокВернуться к началу урокаВыбрать урок
- 41. УРОК 5Повторение и обобщение знаний по теме «Методы решения диофантовых уравнений»Начать
- 42. УРОК 5Тема: Повторение и обобщение знаний по
- 43. УРОК 5 На предыдущих уроках были рассмотрены 6
- 44. УРОК 5РешениеОдна четырехтонная машина может взять 32
- 45. УРОК 5Возможно ли найти квадрат числа, который
- 46. УРОК 5Килограмм яблок стоит 2 гривны, килограмм
- 47. УРОК 5 На этом уроке были получены навыки
- 48. УРОК 5 ЗАВЕРШЕНВернуться к началу урокаВыбрать урок
Слайд 2СПИСОК УРОКОВ
Урок 1.
Понятие диофантовых уравнений. Теоремы.
Урок 2.
Методы решения диофантовых
Урок 3.
Решение диофантовых уравнений, как квадратных. Использование тождественные преобразований.
Урок 4.
Метод от противного. Метод остатков. Метод параметризации.
Урок 5.
Повторение и обобщение знаний по теме «Методы решения диофантовых уравнений»
Слайд 4УРОК 1
Тема: Понятие диофантовых уравнений. Теоремы.
Цель: изучить понятие диофантовых уравнений; доказать
Ход урока
С уравнениями в математике (да и в повседневной жизни) нам приходится сталкиваться постоянно. В школьном курсе рассматривают далеко не все из огромного множества уравнений.
Немного подзабытыми и недостаточно изученными остаются диофантовы (неопределенные) уравнения. Скорее всего, каждому из нас приходилось не один раз решать уравнения в целых числах, возможно, даже не задумываясь над этим.
Далее
Слайд 5УРОК 1
Попытаемся решить следующую задачу:
Покупка свитера.
Вы должны уплатить за купленный в
Комментарии
Слайд 6УРОК 1
Попытаемся решить следующую задачу:
Покупка свитера.
Вы должны уплатить за купленный в
Комментарии
Вопрос задачи сводится к тому, чтобы узнать, сколько вы должны дать кассиру трехрублевок, чтобы, получив сдачу пятирублевками, уплатить 19 рублей. Неизвестных в задаче два - число трехрублевок, пусть их будет x, и число пятирублевок, пусть их будет y. Но составить мы можем лишь одно уравнение: 3x-5y=19
Хотя одно уравнение с двумя неизвестными имеет бесчисленное множество решение, но отнюдь еще не очевидно, что среди них найдется хоть одно с целыми положительными x и y. Вот мы и пришли к задаче, решаемой диофантовым уравнением.
Далее
Слайд 7УРОК 1
Итак, обозначим понятие диофантового уравнения.
Диофантовы уравнения – это алгебраические уравнения
Историческая справка
Общий вид дифантового уравнения c двумя неизвестными: ax+by=c. Например, 5x+8y=39, x2-3y2=1
Перейти к упражнению
Слайд 8УРОК 1
Задание 1. Определите, является ли диофантовым уравнение. Аргументировать свой ответ.
71x-9y=1
5x+8y=2,6
x2+y2=9
5,1x+4,6y2=8
6y+13x-2z=8
-9x+17z=0
Примечание:
Далее
Слайд 9УРОК 1
Термин диофантовы уравнения берет свое начало от имени выдающегося греческого
Если в этой задаче приведены действительные факты, то, значит, Диофант женился в 33 года, у него был сын, умерший в среднем возрасте, а сам Диофант дожил до 84 лет.
Далее
Слайд 10УРОК 1
До нашего времени, дошла примерно половина (6 из 13 книг)
Поскольку большинство задач в этой книге предусматривают решения в целых числах, то для анализа подобного рода проблем стал применяться термин диофантов.
Сегодня диофантов анализ - это обширная, сложная область теории чисел, которой посвящена многочисленная научная литература.
Перейти к заданию
Слайд 11УРОК 1
Теперь, выясним, всегда ли возможно решить неопределенное уравнение в целых
Теорема 1
Если свободный член неопределенного уравнения ax+by=c не делится на наибольший общий делитель коэффициентов a и b , то уравнение не имеет целых решений.
Теорема 2
Если коэффициенты a и b неопределенного уравнения ax+by=c являются взаимно простыми числами, то уравнение имеет, по крайней мере, одно целое решение.
Теорема 1 утверждает, что условие НОД(a;b)=1 является необходимым условием для разрешимости неопределенного уравнения ax+by=c в целых числах. Теорема 2 утверждает, что это условие является достаточным.
Далее
Слайд 12УРОК 1
Задание 2. Используя вышеприведенные теоремы определите, имеют ли решения следующие
6x+12y=13
6x+7y=14
18y+9z=82
7x+4y=56
x+2y=1
Далее
Слайд 15УРОК 2
Тема: Методы решения диофантовых уравнений. Метод спуска или рессеивания.
Цель: узнать
Ход урока
Неопределенные уравнения встречаются как в задачах Вавилона и Египта (II тыс. до н.э.), так и в трудах древнегреческих, китайских, индийских учёных. Они присутствуют в старинных русских и арабских задачах. Впервые решением неопределённых уравнений в целых числах занимались учёные Индии (V – XII вв.), предложившие общий метод для решения в целых числах неопределенных уравнений I степени с целыми коэффициентами, некоторых неопределенных уравнений II степени с двумя неизвестными.
Далее
Слайд 16УРОК 2
В теории чисел созданы специальные методы решения диофантовых уравнений. Общая
В исследовании диофантовых уравнений выше второй степени были достигнуты серьезные успехи лишь в 20 веке. Существует много направлений теории диофантовых уравнений. Так, известной задачей теории диофантовых уравнений является Великая теорема Ферма. Над теориями диофантовых уравнений трудились и другие математики: А. Туэ, Д.К. Фадеев, Б.Н. Делоне и другие.
Леонард Эйлер
Пьер Ферма
Далее
Слайд 17УРОК 2
Наиболее сложной задачей диофантового анализа является правильный выбор алгоритма решения
Далее
Слайд 18УРОК 2
На этом уроке мы научимся решать диофантовы уравнения первой степени.
Напомним условие задачи:
Вы должны уплатить за купленный в магазине свитер 19 рублей. У вас одни лишь трехрублевки, у кассира - только пятирублевки. Можете ли вы при наличии таких денег расплатиться с кассиром и как именно?
Далее
Слайд 19УРОК 2
Решение
Выразим x через у:
Так как x, у,6 –
Обозначим это выражение буквой t. Тогда x=6+y+t, где t=(1+2y)/3, значит 3t=1+2y, а 2y=3t-1.
Поэтому y=(3t-1)/2=t+(t-1)/2.
Так как y, t – целые число, то и (t-1)/2 должно быть целым числом t1. Тогда y=t+ t1 , где t1 = (t-1)/2, значит 2 t1=t-1 и t=2 t1+t.
Значение t=2 t1+t подставляем в предыдущие равенства:
y=t+t1=(2t1+1)+t1=3t1+1
x=6+y+t=6+(3t1+1)+(2t1+1)=8+5t1
Итак, мы нашли выражения для x и y. Мы знаем, что эти числа не только целые, но и положительные:
8+5t1>0 и 3t1+1>0. Решив неравенства, заключаем, что t1=0, 1, 2, 3…
Соответствующие значения x = 8, 13, 18, 23, a y=1, 4, 7, 10…
Уравнение решено.
Далее
Слайд 20УРОК 2
Задание 3. Самостоятельно закончите решение задачи, интерпретировав ответ
Решая задачу
Теорема 3
Диофантовы уравнения вида ax+by=c, где a,b,c – целые числа, а также a и b – взаимно простые, имеет следующий ряд решений: если x0 и y0 – одно решение, то числа x=x0+bn, y=y0-an (n – любое число) тоже будут решениями.
Доказательство
Подставим в данное диофантово уравнение значение x и y. Получим a(x0+bn)+b(y0-an)=c
Раскроем скобки и приведем подобные
ax0 +abn+by0-ban=c
ax0 +by0=c
Что и требовалось доказать.
Далее
Слайд 21УРОК 2
Таким образом, используя формулы и рассуждения можно без особых усилий
Задание 4. Самостоятельно найдите не менее четырех целых решений уравнений.
5x+8y=39
8x-5y=19
7x-5y=1
32x+20y=1076
Примечание: первое решение уравнений попытайтесь подобрать устно, а следующие найдите по формулам
Далее
Слайд 23УРОК 3
Решение диофантовых уравнений, как квадратных. Использование тождественные преобразований.
Начать
Слайд 24УРОК 3
Тема: Решение диофантовых уравнений, как квадратных. Использование тождественные преобразований
Цель: научиться
Ход урока
Сначала необходимо вспомнить последовательность разложения выражений на множители:
Способ группировки
Вынесение общего множителя за скобки
Применение формул сокращенного умножения
Далее
Слайд 25УРОК 3
Метод спуска бесспорно удобен и наиболее прост для решения уравнений
Рассмотрим этот метод, найдя все целые числа, которые являются решениями уравнения xy-3x+5y=25
Далее
Слайд 26УРОК 3
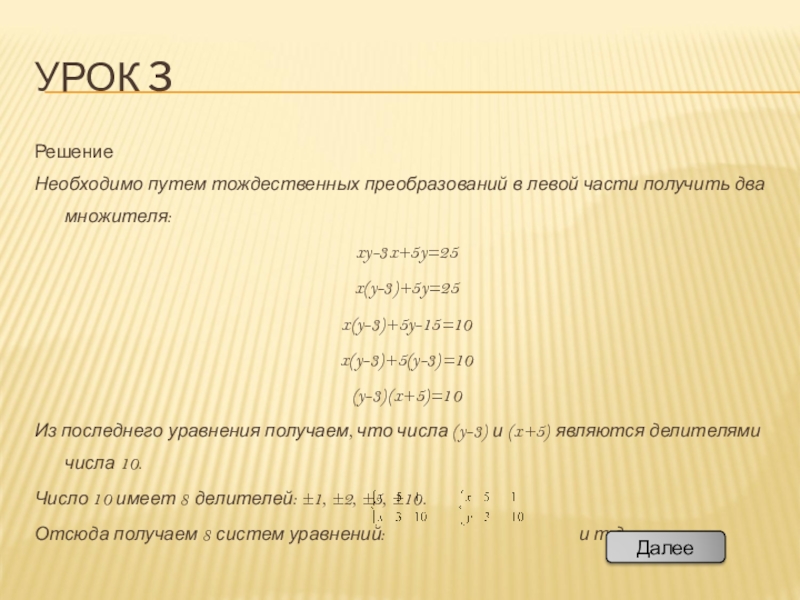
Решение
Необходимо путем тождественных преобразований в левой части получить два множителя:
xy-3x+5y=25
x(y-3)+5y=25
x(y-3)+5y-15=10
x(y-3)+5(y-3)=10
(y-3)(x+5)=10
Из
Число 10 имеет 8 делителей: ±1, ±2, ±5, ±10.
Отсюда получаем 8 систем уравнений: и т.д.
Далее
Слайд 27УРОК 3
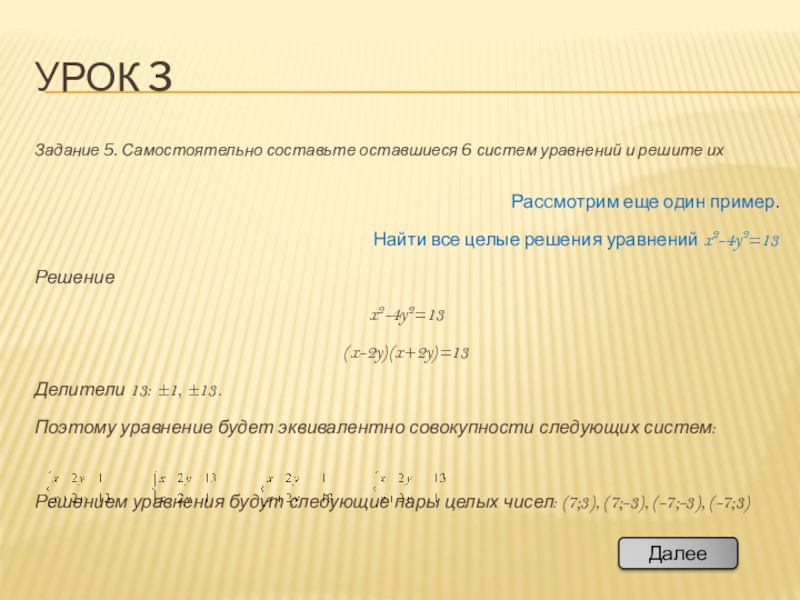
Задание 5. Самостоятельно составьте оставшиеся 6 систем уравнений и решите
Расcмотрим еще один пример.
Найти все целые решения уравнений x2-4y2=13
Решение
x2-4y2=13
(x-2y)(x+2y)=13
Делители 13: ±1, ±13.
Поэтому уравнение будет эквивалентно совокупности следующих систем:
Решением уравнения будут следующие пары целых чисел: (7;3), (7;-3), (-7;-3), (-7;3)
Далее
Слайд 28УРОК 3
В отдельных случаях после тождественных преобразований целесообразно выполнить замену. При
Иногда решение диофантового уравнения путем разложения на множители приводит к громоздким преобразованиям и является трудоемкой работой. В некоторых из этих случаев можно решить уравнение более изящным способом – рассмотреть уравнение, как квадратное относительно какой-либо переменной.
Решите уравнение в целых числах 3(x2+xy+y2)=x+8y
Далее
Слайд 29УРОК 3
Рассмотрим уравнение, как квадратное относительно x
3x2+3xy+3y2-x-8y=0
3x2+3xy-x+3y2-8y=0
3x2+(3y-1)x+3y2-8y=0
D=(3y-1)2-4*3*(3y2-8y)=9y2-6y+1-36y2+96y=-27y2+90y+1
Данное уравнение имеет корни, если
-27y2+90y+1≥0
27y2-90y-1≤0
D/4=452+27=2052
Итак, у находится в промежутке
Так как значение у только целые, то условию удовлетворяет числа 0, 1, 2, 3.
Перебирая значения получим две пары ответов: (0;0) и (1;1)
Далее
Слайд 30УРОК 3
Задание 6. Самостоятельно найдите все решения уравнений в множестве целых
xy+3x-5y=-3
x2-9y2=19
x3+y3=35
Примечание: используете формулы сокращенного умножения
Далее
Слайд 33УРОК 4
Тема: Метод от противного. Метод остатков. Метод параметризации
Цель: изучить и
Ход урока
Методы, которые будут рассмотрены на этом уроке используют для доказательства бесконечности или отсутствия решений диофантового уравнения. Нередко эти методы требуют смекалки и находчивости.
В первую очередь обратимся к методу от противного, который, как мы знаем, есть одним из наиболее общах методов доказательства математических утверждений. Поэтому применение этого метода при решении диофантовых уравнений во многих случаях является эффективным. Итак, пример.
Существуют ли решения уравнения x2-y2=1990 среди целых чисел?
Далее
Слайд 34УРОК 4
Решение
Преобразуем выражение, используя формулу сокращенного умножения:
x2-y2=1990
(x-y)(x+y)=1990
Пусть (x0:y0) – некоторая пара
(x0-y0)(x0+y0)=1990
Числа x0-y0 и x0+y0 – одинаковой четности
Задание 7. Самостоятельно докажите это утверждение
(Примечание: используйте знания о четности чисел)
Если x0-y0 и x0+y0 – одновременно нечетные, то в левой части получим нечетное число (нечетно*нечетное=нечетное), которое не может быть равным четному числу 1990. имеем противоречие.
Если одновременно x0-y0 и x0+y0 четные, то произведение кратно 4, но число 1990 на 4 не делится. Снова пришли к противоречию.
Итак, вывод, уравнение не имеет целых решений.
Далее
Слайд 35УРОК 4
При решении диофантовых уравнений полезно сравнивать остатки, которые дают правая
Тут целесообразно также использовать основные свойства теории конгруэнции (сравнения), то есть сравнивать числа по некоторым модулям. Два целых числа a и b называются конгруэнтами по модулю М, если остатки при делении их на число М равны между собой. Легко заметить, что два числа a и b конгруэнтные по модулю М тогда и только тогда, когда их разность делится на М. Записывается это так: a=b(mod M).
Пример. Существуют ли натуральные числа, которые удовлетворяют уравнению x3-x=3y2+1
Далее
Слайд 36УРОК 4
x3-x=3y2+1
x(x2-1)=3y2+1
(x-1)x(x+1)=3y2+1
Левая часть уравнения как произведение трех последовательных чисел (x-1)и x
Правая часть – число, которое при делении на 3 дает остаток 1, т.к. 3y2 делится на 3, а 1 является остатком).
Итак, уравнение на имеет решений в целых числах
Далее
Слайд 37УРОК 4
При доказательстве бесконечности множества целых решений неопределенных уравнений эффективным методом
Заметим, что метод параметризации не является алгоритмическим.
Далее
Слайд 38УРОК 4
Доказать, что уравнение x2+y2=z2 имеет бесконечное множество целых решений.
Доказательство
Приняв ко
Далее
Слайд 39УРОК 4
Задание 8. Самостоятельно определите имеют ли решения и следующие уравнения.
x2+y3=z4
x2-3y2=-1
x3+y4=z5
x2-z2=2002
Примечание: 1,2: метод остатков; 3: метод параметризации; 4: метод от противного
Далее
Слайд 42УРОК 5
Тема: Повторение и обобщение знаний по теме «Методы решения диофантовых
Цель: повторить и обобщить знания по теме; научиться решать задачи, приводящие к диофантовым уравнениям
Ход урока
Вопросы для проверки теоретических знаний:
Какие уравнения называют диофантовыми?
Какое условие является необходимым для разрешимости неопределенного уравнения ax+by=c? А какое достаточным?
В основу какого метода положен процесс построения бесконечной нисходящей последовательности целых слагаемых чисел?
Перечислите изученные методы решения.
Далее
Слайд 43УРОК 5
На предыдущих уроках были рассмотрены 6 методов используемых при решении
Несколько четырехтонных и 2,5-тонных машин должны перевести 1076 плит. Вес плиты 125 кг. Сколько требуется машин обоих видов, чтобы совершить как можно меньше рейсов?
Далее
Слайд 44УРОК 5
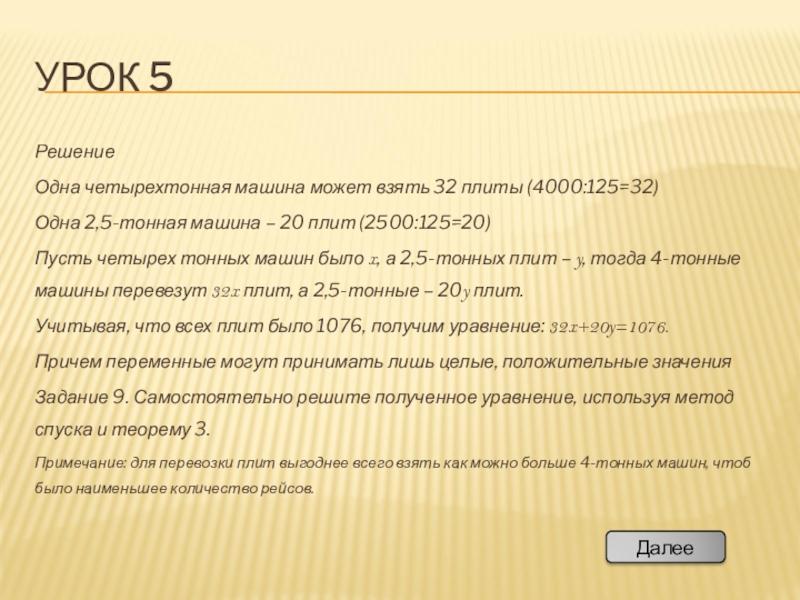
Решение
Одна четырехтонная машина может взять 32 плиты (4000:125=32)
Одна 2,5-тонная машина
Пусть четырех тонных машин было x, а 2,5-тонных плит – y, тогда 4-тонные машины перевезут 32x плит, а 2,5-тонные – 20y плит.
Учитывая, что всех плит было 1076, получим уравнение: 32x+20y=1076.
Причем переменные могут принимать лишь целые, положительные значения
Задание 9. Самостоятельно решите полученное уравнение, используя метод спуска и теорему 3.
Примечание: для перевозки плит выгоднее всего взять как можно больше 4-тонных машин, чтоб было наименьшее количество рейсов.
Далее
Слайд 45УРОК 5
Возможно ли найти квадрат числа, который в сумме с кубом
Решение
Итак, вопрос стоит так: имеет ли решение x2+y3=z4 решения во множестве простых чисел. Пусть x,y,z – простые решения данного уравнения…
Задание 10. Самостоятельно решите полученное уравнение используя метод остатков.
Далее
Слайд 46УРОК 5
Килограмм яблок стоит 2 гривны, килограмм слив 3 гривны, а
Решение
Обозначим через x,y и z количество килограмм яблок, слив и персиков соответственно. По условию задачи:
Выразим из второго уравнения переменную x и решим систему способом подстановки. В этом уравнении разыскиваются натуральные значения переменных или 0
Задание 11. Самостоятельно решите полученное уравнение используя четность чисел
Далее
Слайд 47УРОК 5
На этом уроке были получены навыки по решению задач, приводящим
Рекомендуется также рассмотреть решения частных случаев диофантовых уравнений (в работе), которые применяется еще несколько специфических приемов решения.
Далее