- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 9 класса по теме Корень п-ой степени
Содержание
- 1. Презентация по математике для 9 класса по теме Корень п-ой степени
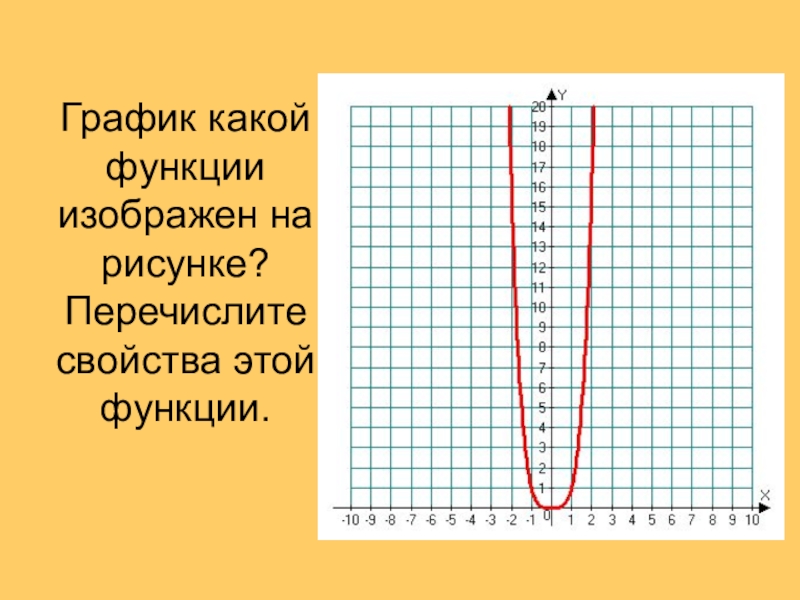
- 2. График какой функции изображен на рисунке? Перечислите свойства этой функции.
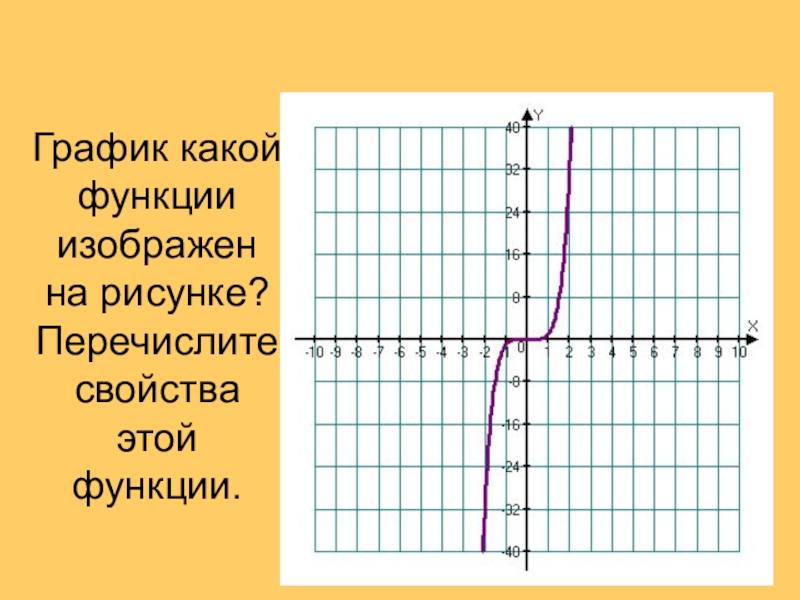
- 3. График какой функции изображен на рисунке? Перечислите свойства этой функции.
- 4. Функция задана формулой
- 5. Функция задана формулой
- 6. Корень n - ой степени
- 7. Повторение: Что называется квадратным
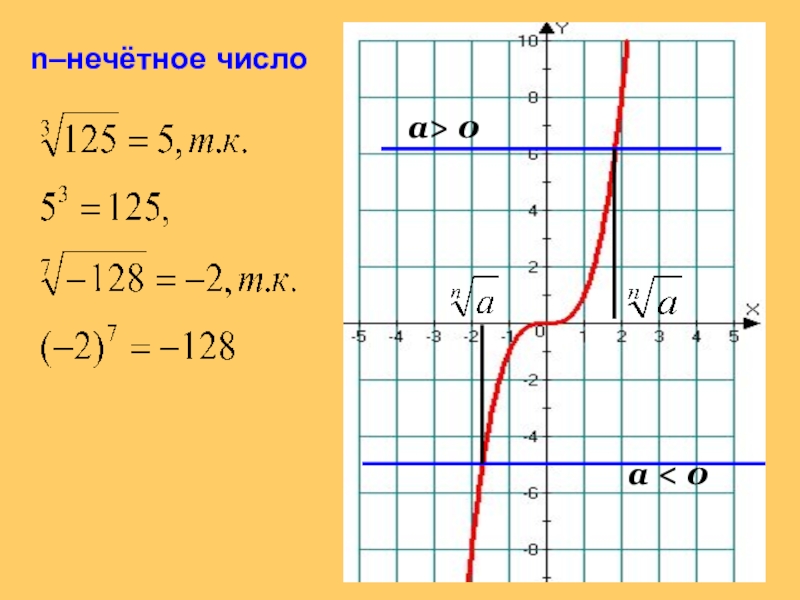
- 8. а> 0а < 0n–нечётное число
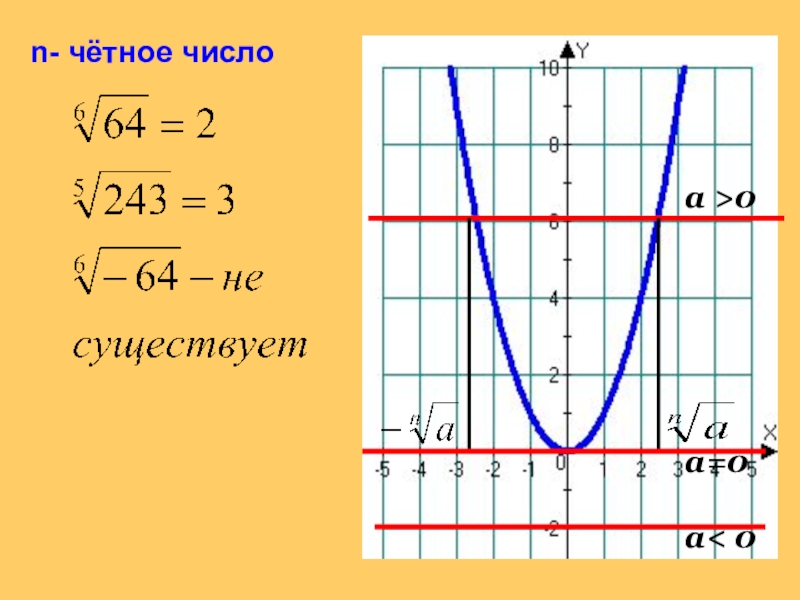
- 9. n- чётное числоа >0а=0а< 0
- 10. Вывод: Если n- нечётное число, то выражение
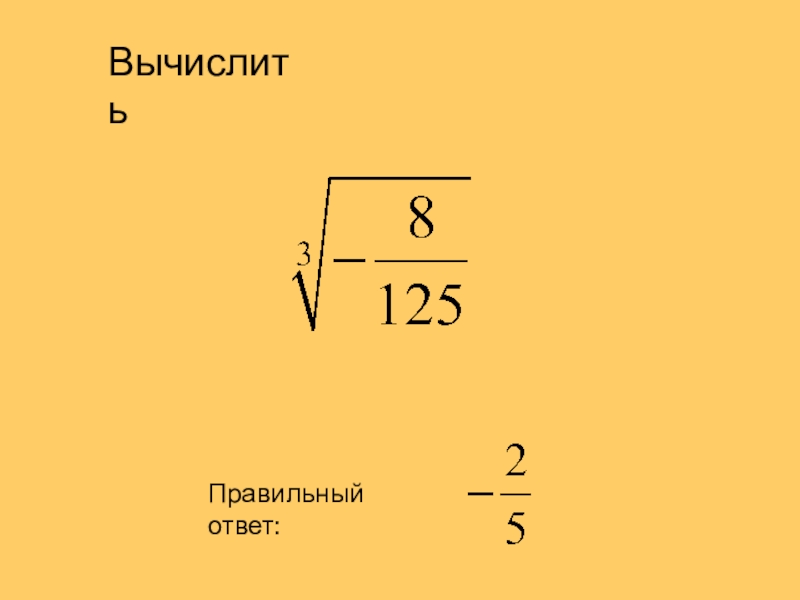
- 11. ВычислитьПравильный ответ:
- 12. Правильный ответ:Вычислить
- 13. Правильный ответ:Вычислить
- 14. Правильный ответ:Вычислить
- 15. Правильный ответ:Вычислить
- 16. Правильный ответ:Решить уравнение
- 17. Правильный ответ:Решить уравнение
- 18. При каких значениях х имеет смыслвыражение Правильный ответ:
- 19. При каких значениях х имеет смыслвыражение Правильный ответ:
- 20. При каких значениях х имеет смыслвыражение Правильный ответ:Х > -2
Слайд 1Презентация по алгебре учителя математики МКОУ СОШ №1 пгт. Палана Камчатский край Учебник алгебры 9 класс. Авторы:
Слайд 4Функция задана формулой .
f(3,7) f(3,8)
f(12,4) f(12,2)
f(-2,8) f(-2,9)
f(8,7) f(7,8)
f(-4,5) f(-4,8)
f(1,7) f(-3,8)
f(-5,7) f(5,2)
>
<
<
<
<
>
>
Слайд 5Функция задана формулой .
f(3,7) f(3,8)
f(12,4) f(12,2)
f(-2,8) f(-2,9)
f(8,7) f(7,8)
f(-4,5) f(-4,8)
f(1,7) f(-3,8)
f(-5,7) f(5,2)
>
<
>
>
>
>
<
Слайд 7Повторение: Что называется квадратным корнем из числа а
Квадратным корнем из числа а называется такое число, квадрат которого равен а
Определение: Корнем n-й степени из числа а называется такое число, n-ая степень которого равна а.
Примеры: корнем 5-й степени из числа 32 является число 2, так как 25 = 32; корнем 5-й степени из числа -32 является число -2, так как (-2)5 = -32; корнем 4-й степени из числа 81 являются числа -3 и 3,т. к. (-3)4 = 81 и 34 = 81.
Слайд 10Вывод:
Если n- нечётное число, то выражение
число, то выражение имеет смысл лишь при а ≥ 0.
Из определения корня n –й степени следует, что при всех значениях а, при
которых выражение имеет смысл,
верно равенство