- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 10-11 классов по теме Производная функции. Геометрический смысл производной
Содержание
- 1. Презентация по математике для 10-11 классов по теме Производная функции. Геометрический смысл производной
- 2. Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
- 3. Производная— это скорость изменения функции.
- 4. На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
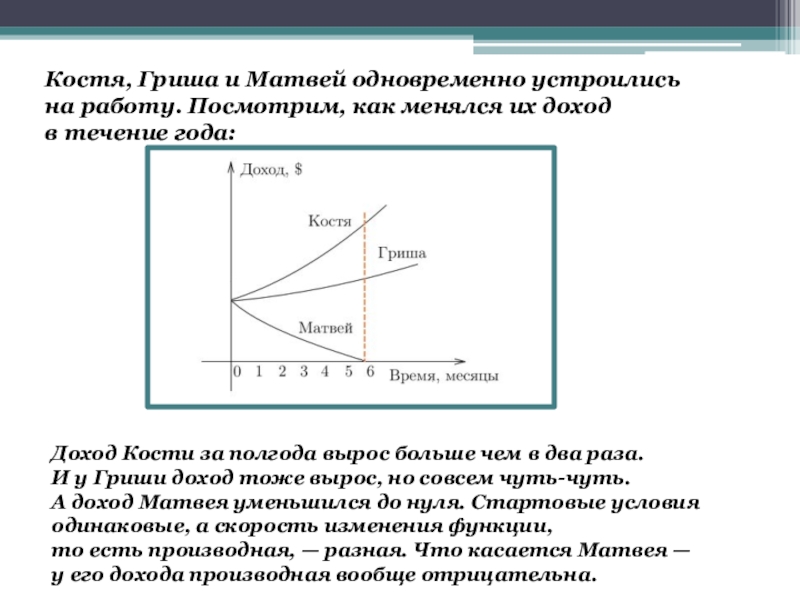
- 5. Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим,
- 6. Интуитивно мы без труда оцениваем скорость изменения функции.
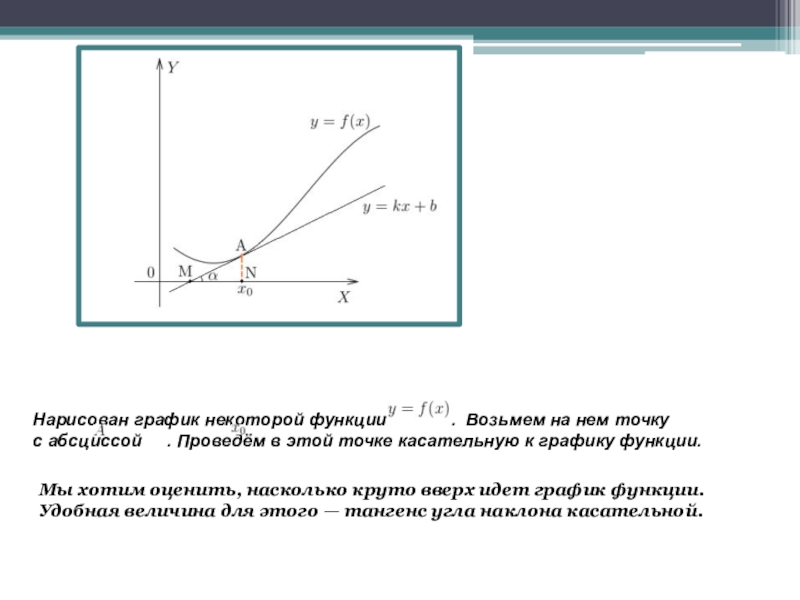
- 7. Нарисован график некоторой функции
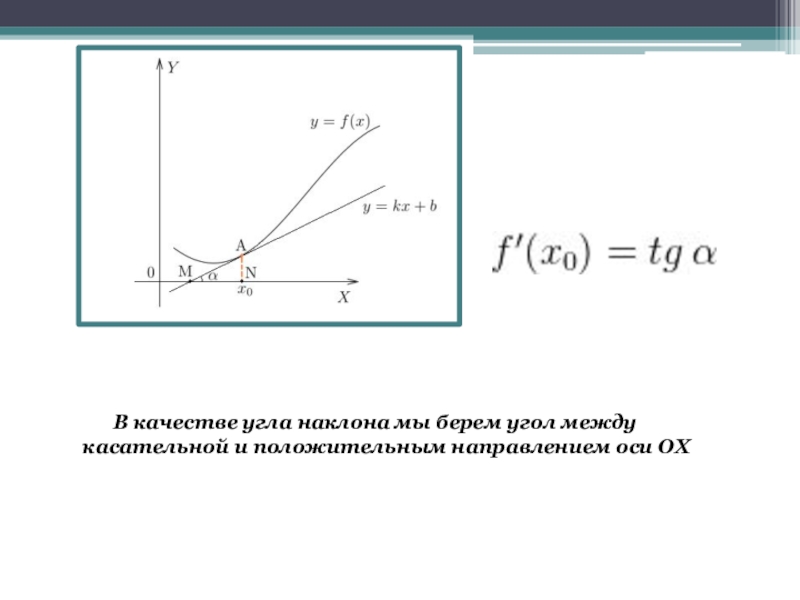
- 8. В качестве угла наклона
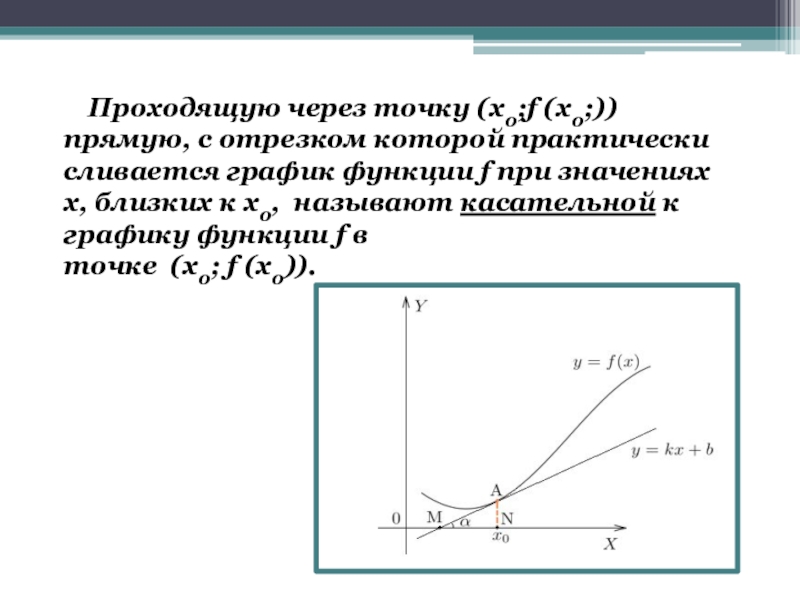
- 9. Проходящую через точку (x0;f
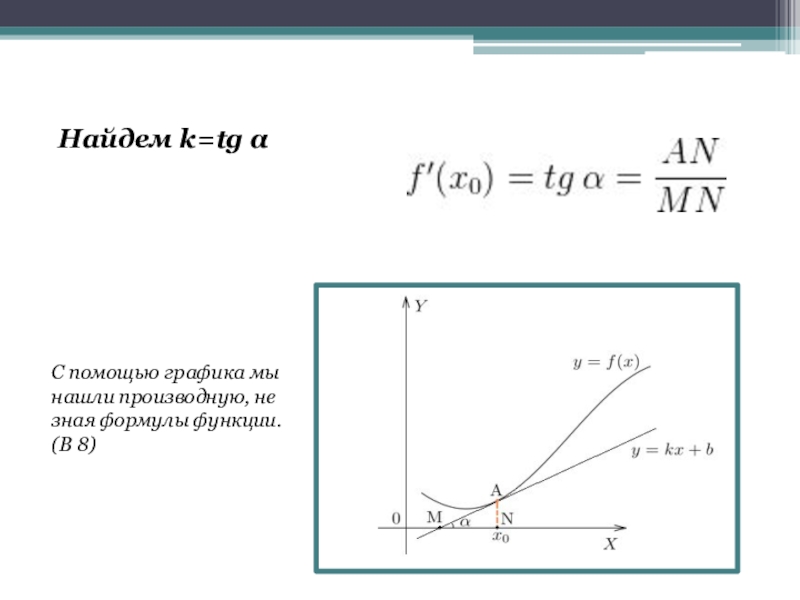
- 10. Найдем k=tg αС помощью графика мы нашли производную, не зная формулы функции.(В 8)
- 11. Производная функции в точке равна угловому
- 12. У одной и той же функции в разных точках может быть
- 13. В точке А функциявозрастает. Касательнаяобразует
- 14. В точках максимума и минимума касательная горизонтальна. Следовательно,
- 15. Слайд 15
- 16. Возможен случай, когда производная в
- 17. В точке Е – точке
Слайд 1Производная функции. Геометрический смысл производной.
учитель математики ГОУ СОШ №223
Платова Н.Ю.
Слайд 2Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос,
Слайд 5Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение
Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Слайд 6Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле
Слайд 7Нарисован график некоторой функции . Возьмем
Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Слайд 9 Проходящую через точку (x0;f (x0;)) прямую, с отрезком
точке (х0; f (х0)).
Слайд 11Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику
Производная функции равна тангенсу угла наклона касательной.
Слайд 12У одной и той же функции в разных точках может быть разная производная. Посмотрим, как же
На одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. Кроме того у этой функции есть точки максимума и минимума.
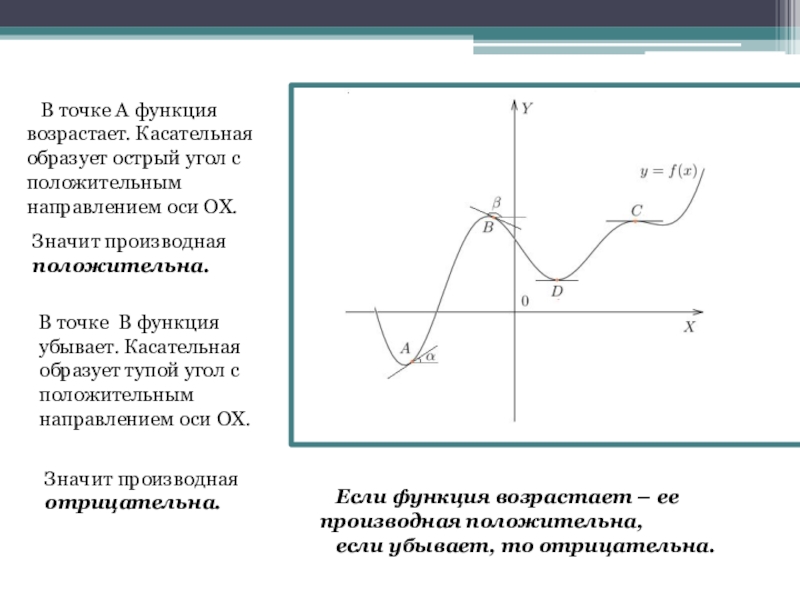
Слайд 13 В точке А функция
возрастает. Касательная
образует острый угол с
положительным
направлением оси
Значит производная
положительна.
В точке В функция
убывает. Касательная
образует тупой угол с
положительным
направлением оси ОХ.
Значит производная
отрицательна.
Если функция возрастает – ее производная положительна,
если убывает, то отрицательна.
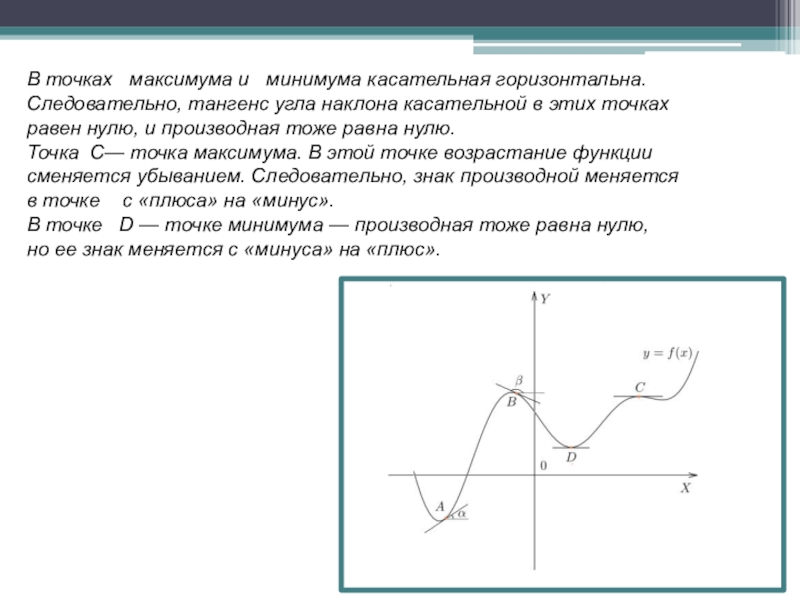
Слайд 14В точках максимума и минимума касательная горизонтальна. Следовательно, тангенс угла наклона касательной
Точка C— точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
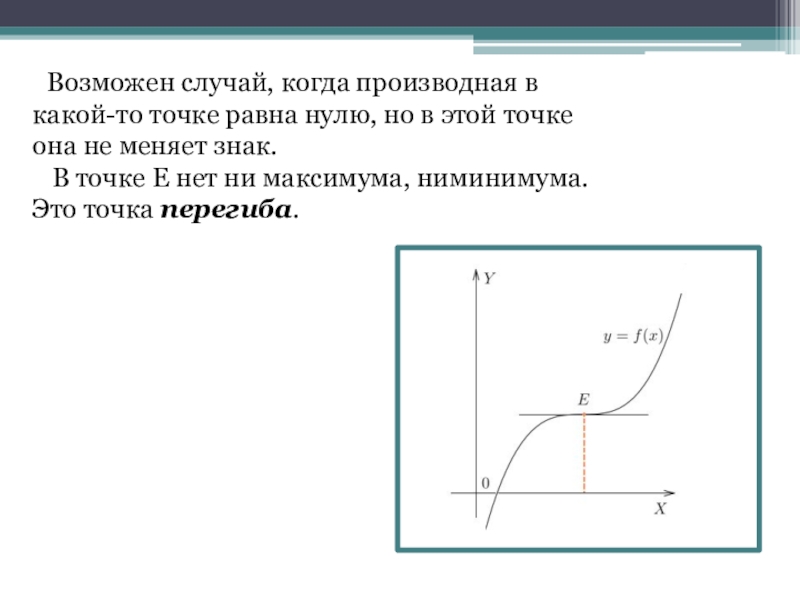
Слайд 16 Возможен случай, когда производная в какой-то точке равна нулю,
В точке Е нет ни максимума, ниминимума. Это точка перегиба.
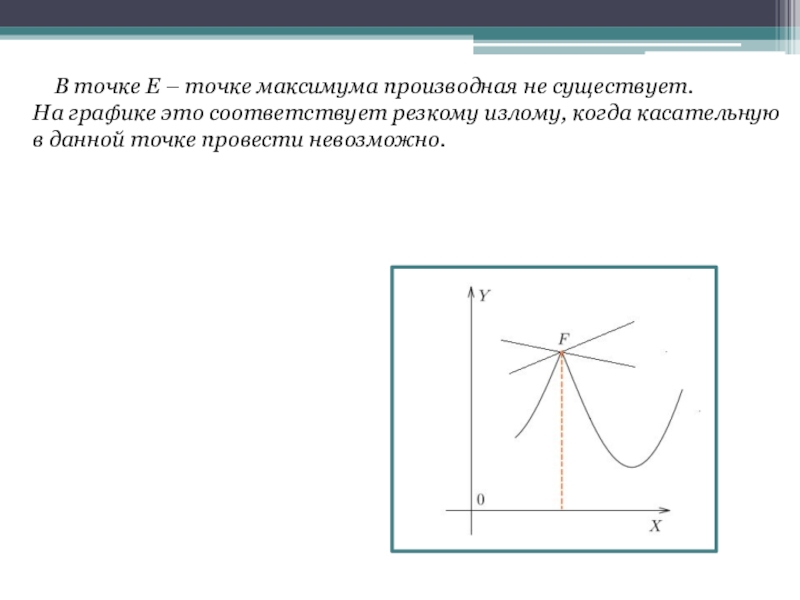
Слайд 17 В точке Е – точке максимума производная не существует.
На
в данной точке провести невозможно.