- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Движения и симметрия 11 класс
Содержание
- 1. Презентация по геометрии на тему Движения и симметрия 11 класс
- 2. Понятие движения Движение – это отображение пространства на себя, сохраняющее расстояния между точками
- 3. Виды движенияЦентральная симметрияОсевая симметрияЗеркальная симметрияПараллельный перенос
- 4. Центральная симметрияЦентральная симметрия — отображение пространства на
- 5. Центральная симметрия является движением. Обозначим буквой О
- 6. Рассмотрим теперь две точки А(х1;
- 7. Слайд 7
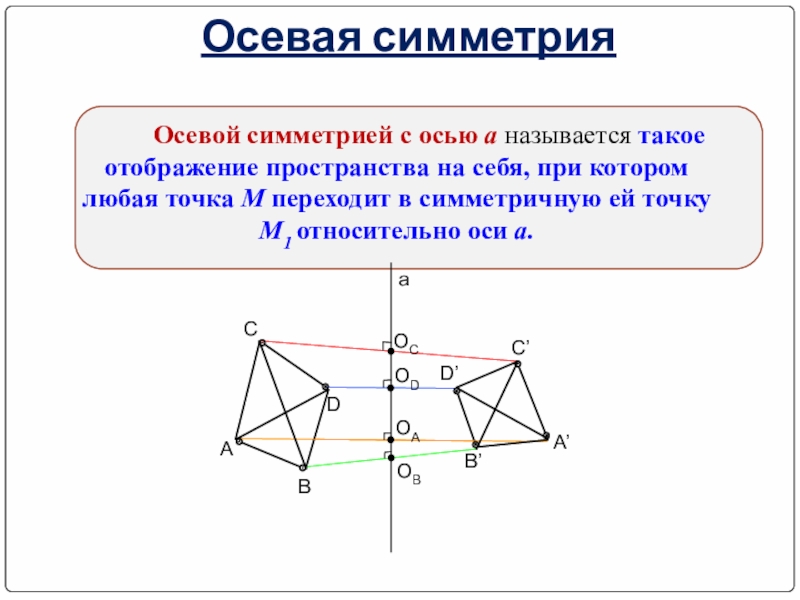
- 8. Осевая симметрияОсевой симметрией с осью а называется
- 9. Осевая симметрия является движением.Для этого введем прямоугольную
- 10. Рассмотрим теперь любые две точки A(х1; у1;
- 11. Слайд 11
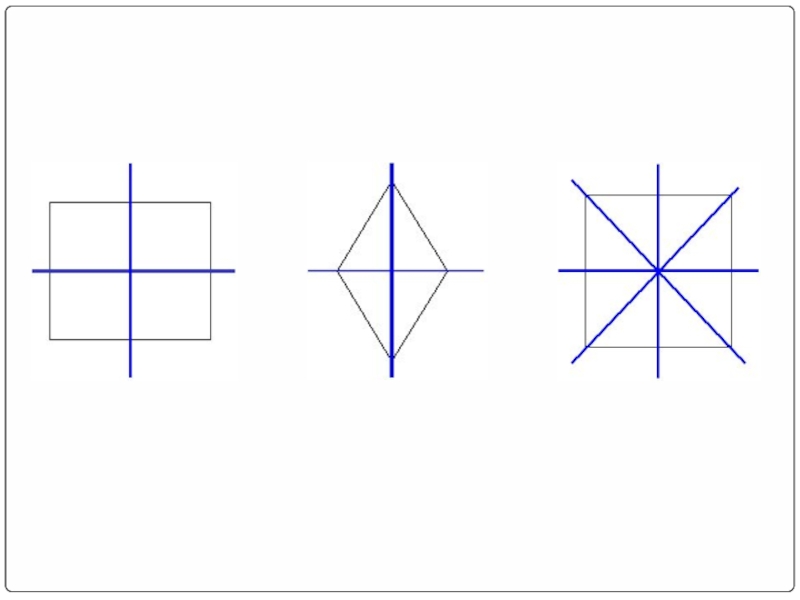
- 12. Осевая симметрия
- 13. Осевая симметрия вокруг нас
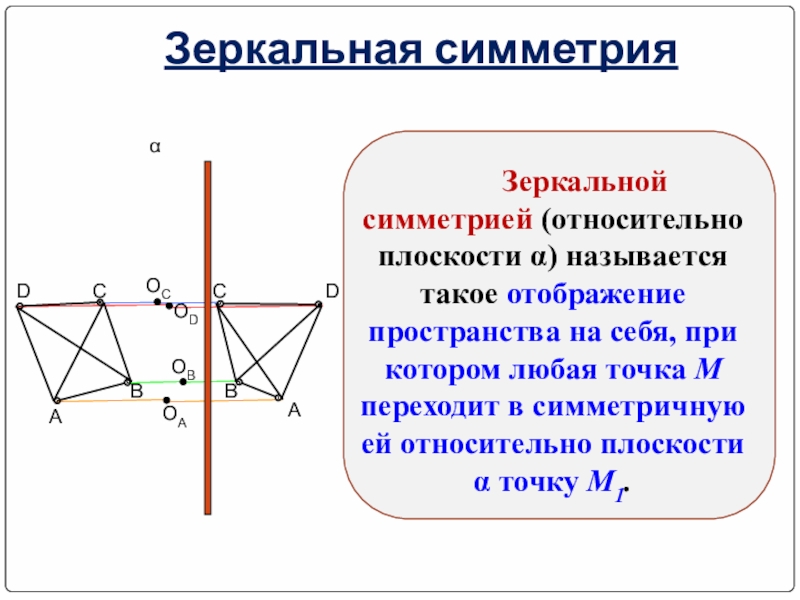
- 14. Зеркальная симметрияЗеркальной симметрией (относительно плоскости α) называется
- 15. Зеркальная симметрия является движением. Для этого введем
- 16. Из первого условия по формуле координат середины
- 17. Рассмотрим теперь две точки А(x1, у1; z1)
- 18. Фигуры, симметричные относительно плоскостиФигура ( тело) называется
- 19. Симметрия в пирамидеВерно ли высказывание: правильная четырехугольная пирамида имеет четыре плоскости симметрии
- 20. Задачи1. Сколько плоскостей симметрии имеет пирамида, в
- 21. Зеркальная симметрия в призме1)Сколько плоскостей симметрии имеет
- 22. Зеркальная симметрия в архитектуре г. Санкт- ПетербургаАлександринский
- 23. Улица Россииимеет плоскость симметрии в общем обзоре, но не все детали в архитектуре зданий симметричны.
- 24. Зеркальная симметрия
- 25. Пример зеркальной симметрииЦентральный зал станции
- 26. Зеркально симметричные объектыОсевая симметрияЗеркальная симметрияЦентральная симметрия
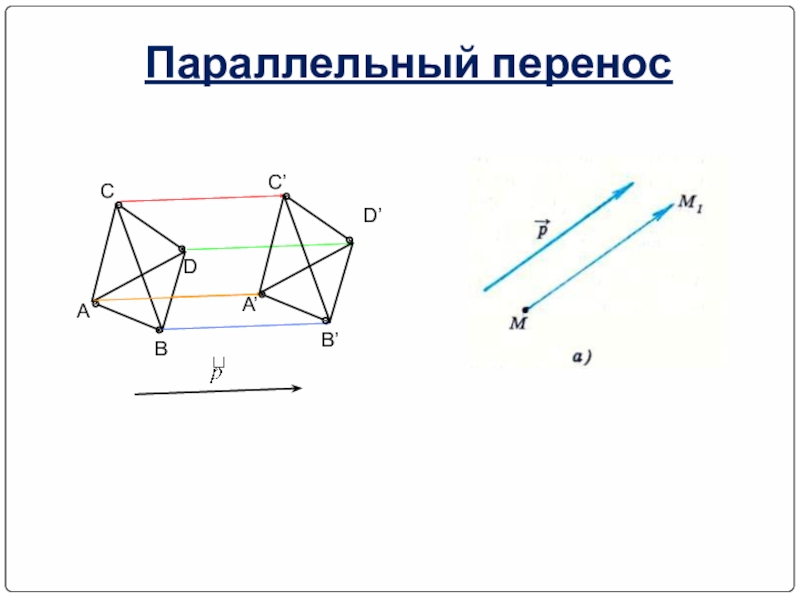
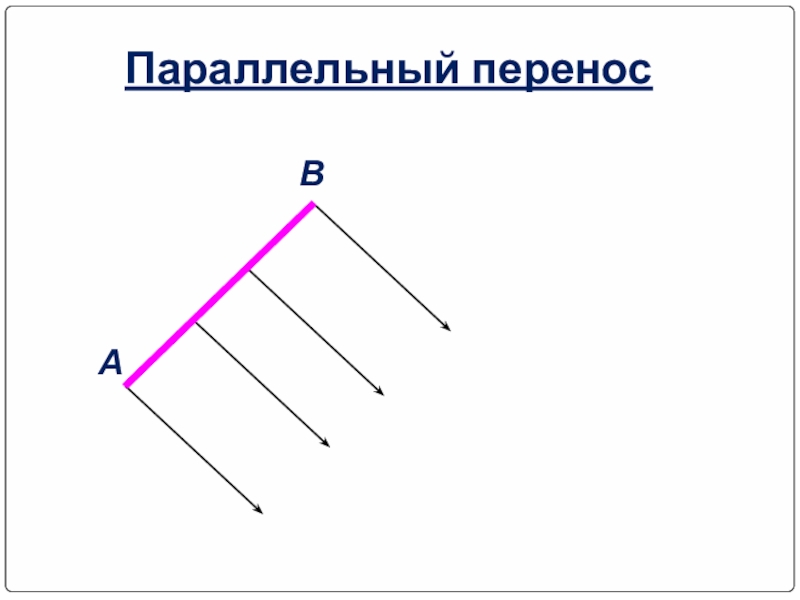
- 27. Параллельный переносПараллельным переносом на вектор р называется
- 28. ABCDA’B’C’D’Параллельный перенос
- 29. Параллельный перенос является движением.При параллельном переносе на
- 30. Параллельный переносНаглядно это
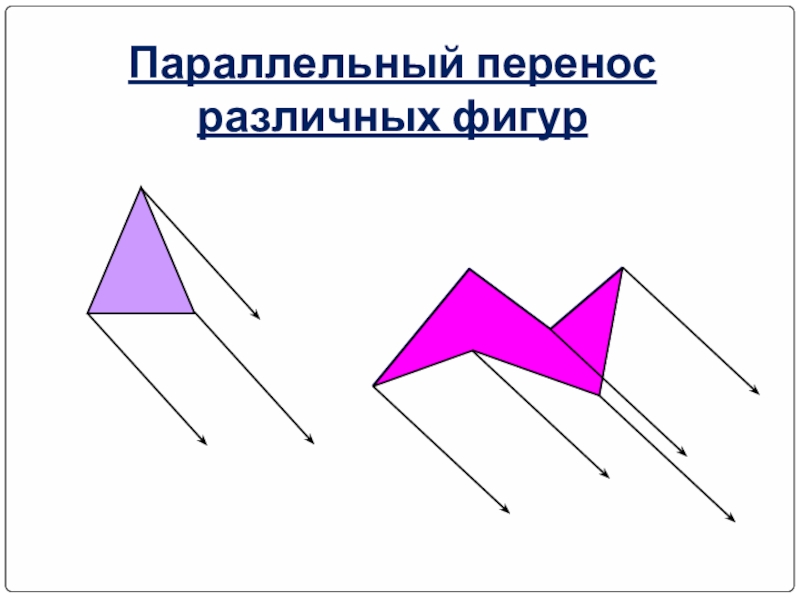
- 31. Параллельный перенос различных фигур
- 32. Параллельный переносАВ
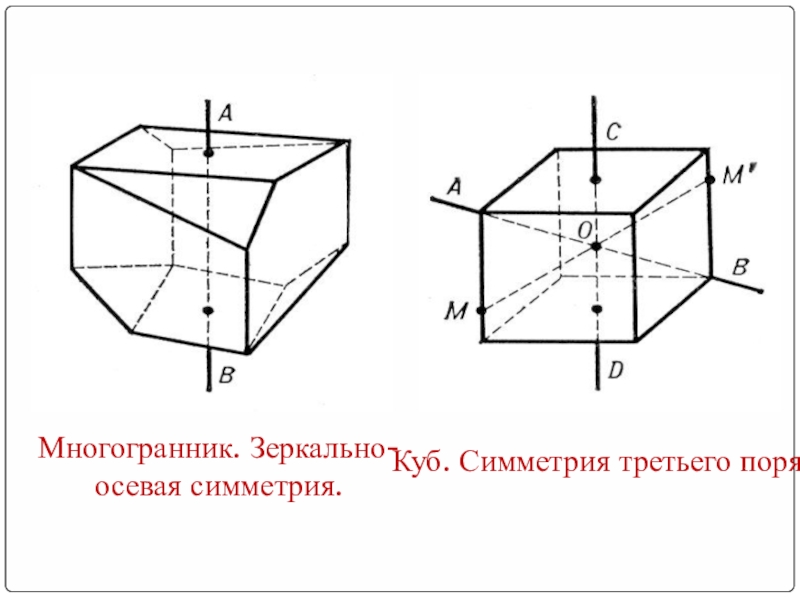
- 33. Многогранник. Зеркально-осевая симметрия.Куб. Симметрия третьего порядка.
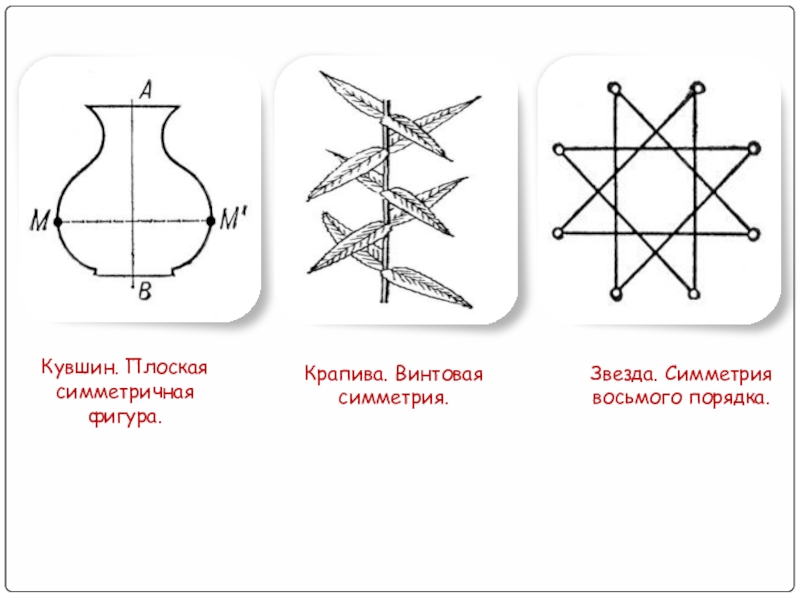
- 34. Кувшин. Плоская симметричная фигура. Крапива. Винтовая симметрия. Звезда. Симметрия восьмого порядка.
- 35. Зеркальная симметрия в природе
- 36. Зеркальная симметрия в природе
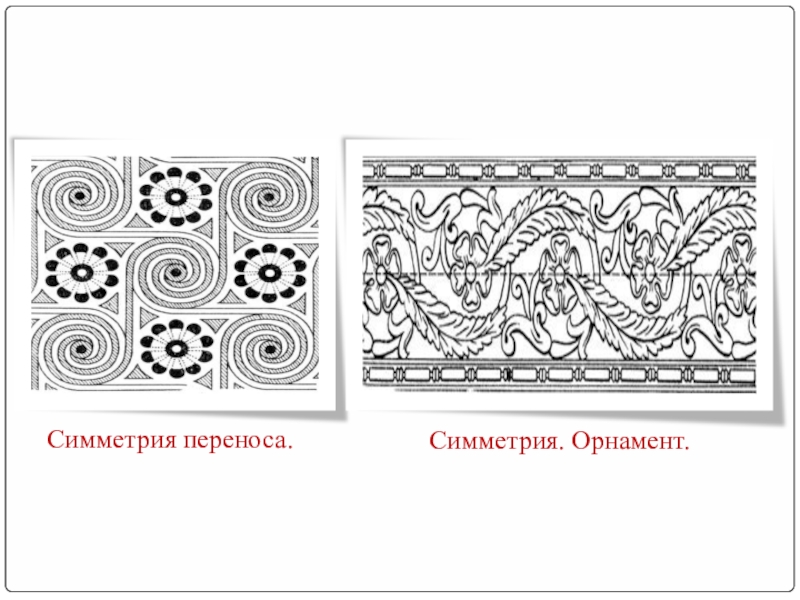
- 37. Симметрия переноса.Симметрия. Орнамент.
Понятие движения Движение – это отображение пространства на себя, сохраняющее расстояния между точками
Слайд 2
Понятие движения
Движение – это отображение пространства на себя, сохраняющее расстояния между
точками
Слайд 4
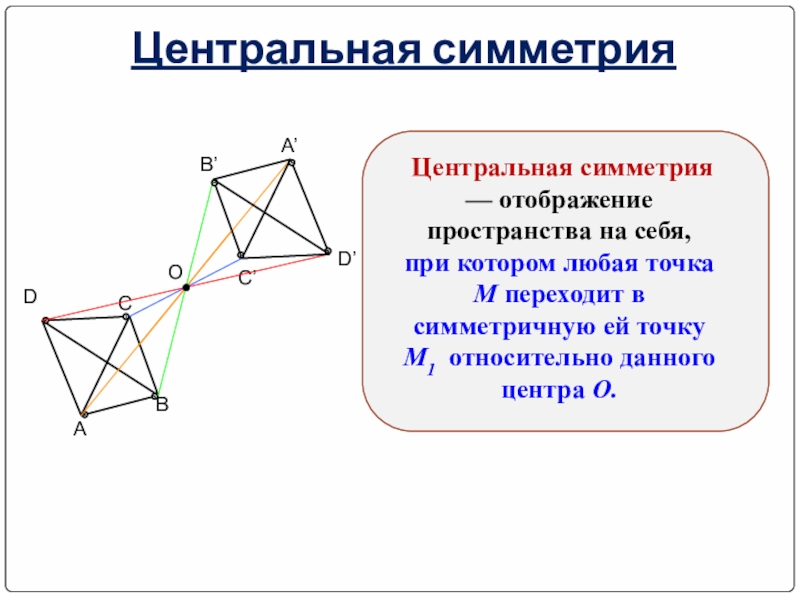
Центральная симметрия
Центральная симметрия — отображение пространства на себя, при котором любая
точка М переходит в симметричную ей точку М1 относительно данного центра О.
Слайд 5
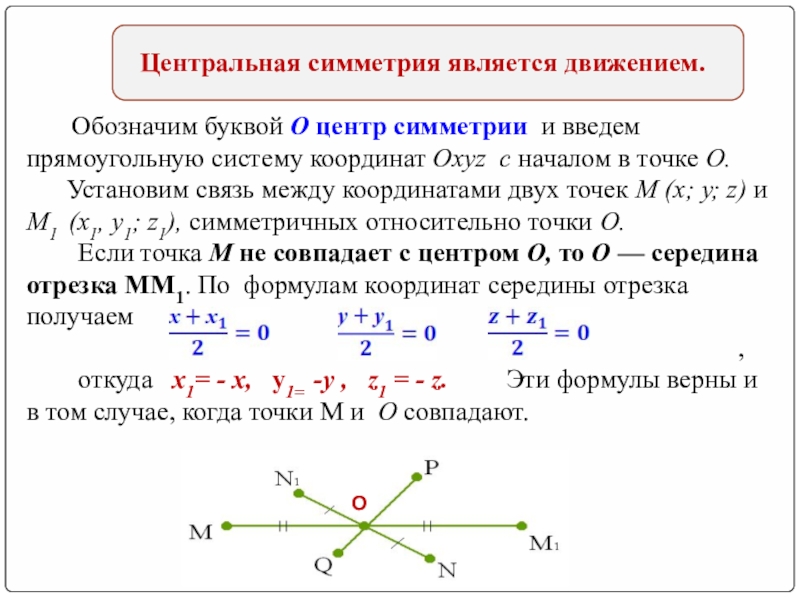
Центральная симметрия является движением.
Обозначим буквой О центр симметрии и введем
прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек М (х; у; z) и М1 (х1, у1; z1), симметричных относительно точки О.
Если точка М не совпадает с центром О, то О — середина отрезка ММ1. По формулам координат середины отрезка получаем
,
откуда х1= - х, у1= -у , z1 = - z. Эти формулы верны и в том случае, когда точки M и О совпадают.
Если точка М не совпадает с центром О, то О — середина отрезка ММ1. По формулам координат середины отрезка получаем
,
откуда х1= - х, у1= -у , z1 = - z. Эти формулы верны и в том случае, когда точки M и О совпадают.
О
Слайд 6
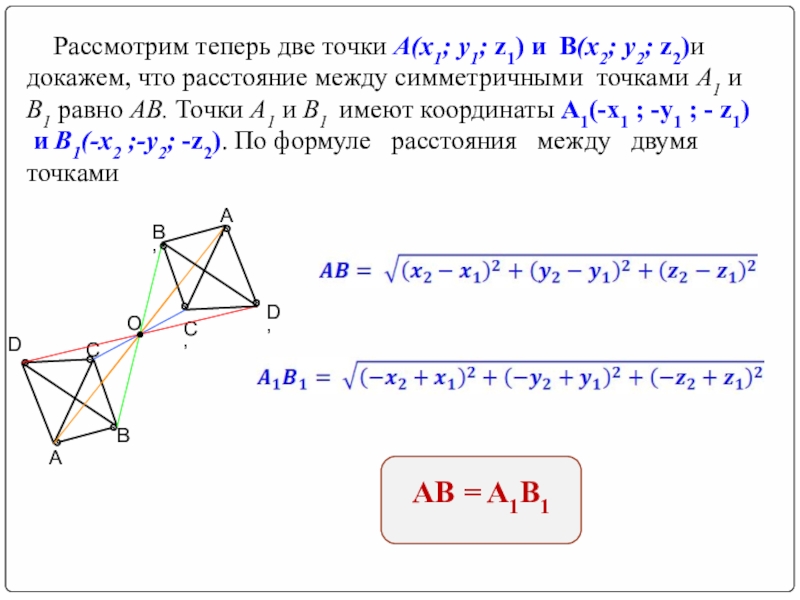
Рассмотрим теперь две точки А(х1; у1; z1) и В(х2;
у2; z2)и докажем, что расстояние между симметричными точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1)
и В1(-х2 ;-у2; -z2). По формуле расстояния между двумя точками
и В1(-х2 ;-у2; -z2). По формуле расстояния между двумя точками
AB = A1B1
Слайд 8
Осевая симметрия
Осевой симметрией с осью а называется такое отображение пространства на
себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.
Слайд 9
Осевая симметрия является движением.
Для этого введем прямоугольную систему координат Oxyz так,
чтобы ось Oz совпала с осью симметрии, и установим связь между координатами двух точек М(х; у; z) и М1(х1, y1; z1), симметричных относительно оси Oz.
Если точка М не лежит на оси Oz , то ось Oz: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна к нему.
Из первого условия по формулам для координат середины отрезка получаем ,
откуда х1= -х и у1 = -у.
Если точка М не лежит на оси Oz , то ось Oz: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна к нему.
Из первого условия по формулам для координат середины отрезка получаем ,
откуда х1= -х и у1 = -у.
Второе условие означает, что аппликаты точек М и М1 равны: z1= z2. Полученные формулы верны и в том случае, когда точка М лежит на оси Oz.
Слайд 10Рассмотрим теперь любые две точки A(х1; у1; z1) и
В(х2; у2;
z2) и докажем, что расстояние между симметричными им точками А1 и В1равно АВ.
Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1) и В1(-х2; -у2; z2).
По формуле расстояния между двумя
точками находим:
Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1) и В1(-х2; -у2; z2).
По формуле расстояния между двумя
точками находим:
AB = A1B1
Слайд 14
Зеркальная симметрия
Зеркальной симметрией (относительно плоскости α) называется такое отображение пространства на
себя, при котором любая точка М переходит в симметричную ей относительно плоскости α точку М1.
Слайд 15
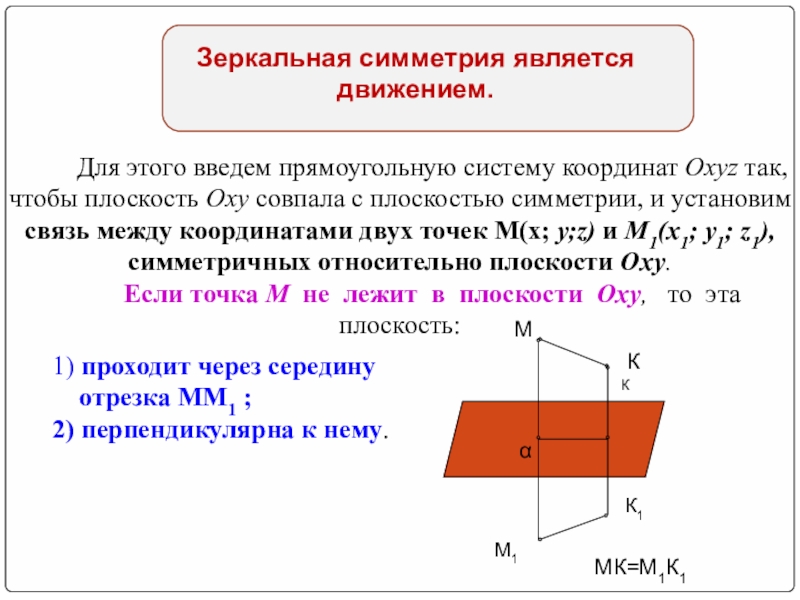
Зеркальная симметрия является движением.
Для этого введем прямоугольную систему координат Oxyz
так, чтобы плоскость Оху совпала с плоскостью симметрии, и установим связь между координатами двух точек М(х; у;z) и М1(х1; у1; z1), симметричных относительно плоскости Оху.
Если точка М не лежит в плоскости Оху, то эта плоскость:
Если точка М не лежит в плоскости Оху, то эта плоскость:
1) проходит через середину
отрезка ММ1 ;
2) перпендикулярна к нему.
М
К
К
α
МК=М1К1
М1
К1
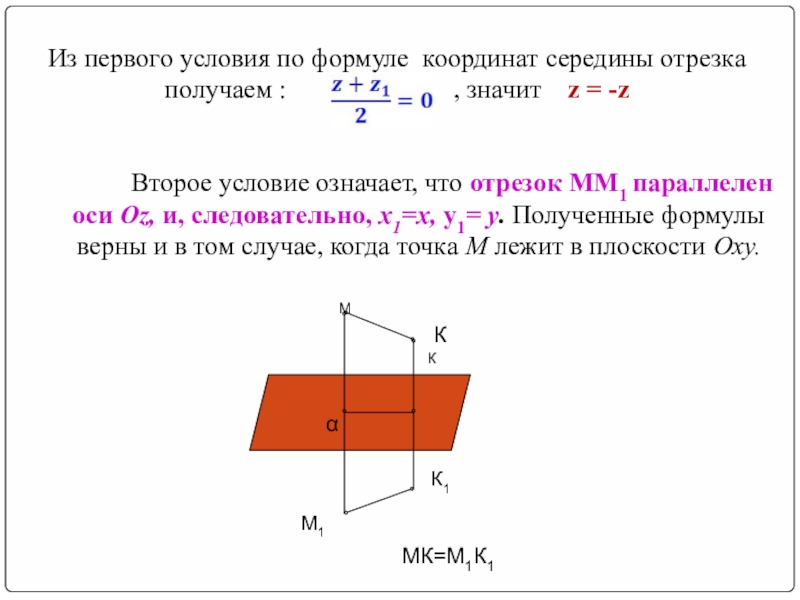
Слайд 16Из первого условия по формуле координат середины отрезка получаем :
, значит z = -z
Второе условие означает, что отрезок ММ1 параллелен оси Oz, и, следовательно, х1=х, у1= у. Полученные формулы верны и в том случае, когда точка М лежит в плоскости Оху.
М
К
К
α
МК=М1К1
М1
К1
Слайд 17Рассмотрим теперь две точки А(x1, у1; z1) и В (х2; у2;
z2) и докажем, что расстояние между симмеричными им точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(х1 ; у1 ; - z1) и В1(х2; у2; -z2). По формуле расстояния между двумя точками находим:
AB = A1B1
Слайд 18
Фигуры, симметричные относительно плоскости
Фигура ( тело) называется симметричной относительно некоторой плоскости,
если эта плоскость разбивает фигуру на две равные симметричные части.
Сколько плоскостей симметрии имеет куб?
Ответы : 2; 4; 5; 6;
9
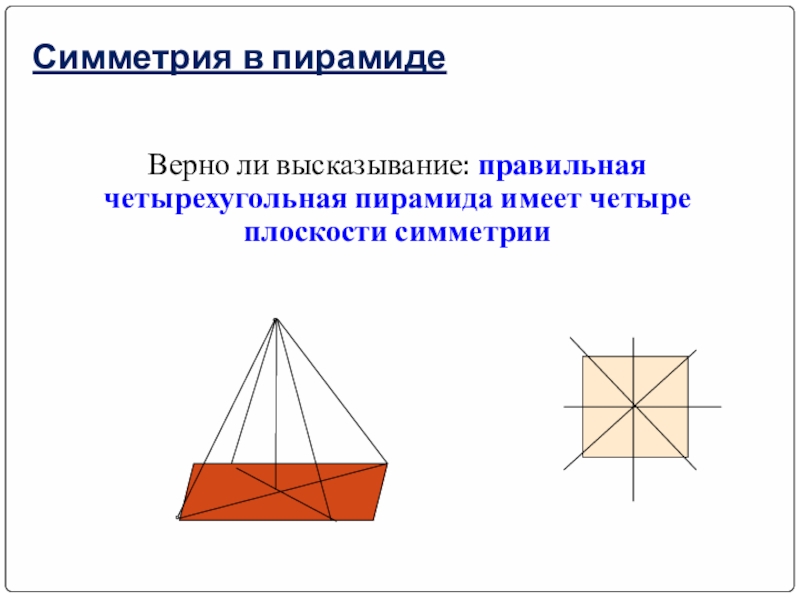
Слайд 19Симметрия в пирамиде
Верно ли высказывание: правильная четырехугольная пирамида имеет четыре плоскости
симметрии
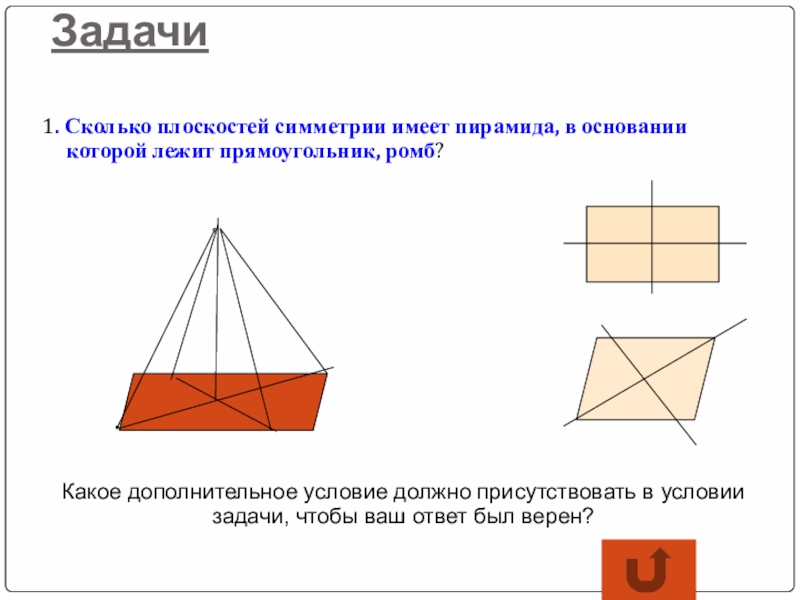
Слайд 20Задачи
1. Сколько плоскостей симметрии имеет пирамида, в основании которой лежит прямоугольник,
ромб?
Какое дополнительное условие должно присутствовать в условии задачи, чтобы ваш ответ был верен?
Слайд 21Зеркальная симметрия в призме
1)Сколько плоскостей симметрии имеет правильная четырехугольная призма?
Ответы:
а)2 б)4 в)3 г)5 д)12
2)Сколько плоскостей симметрии имеет прямая призма, в основании которой лежит прямоугольник?
Ответы:
а)2 б)3 в)1 г)4 д)8
3)Сколько плоскостей симметрии имеет правильная треугольная призма?
Ответы:
а)4 б)3 в)1 г)2 д)5
а)2 б)4 в)3 г)5 д)12
2)Сколько плоскостей симметрии имеет прямая призма, в основании которой лежит прямоугольник?
Ответы:
а)2 б)3 в)1 г)4 д)8
3)Сколько плоскостей симметрии имеет правильная треугольная призма?
Ответы:
а)4 б)3 в)1 г)2 д)5
г) 5
б) 3
а) 4
Слайд 22Зеркальная симметрия в архитектуре г. Санкт- Петербурга
Александринский
театр
Исаакиевский собор
Сколько плоскостей симметрии имеют данные объекты?
Слайд 23Улица России
имеет плоскость симметрии в общем обзоре, но не все детали
в архитектуре зданий симметричны.
Слайд 27
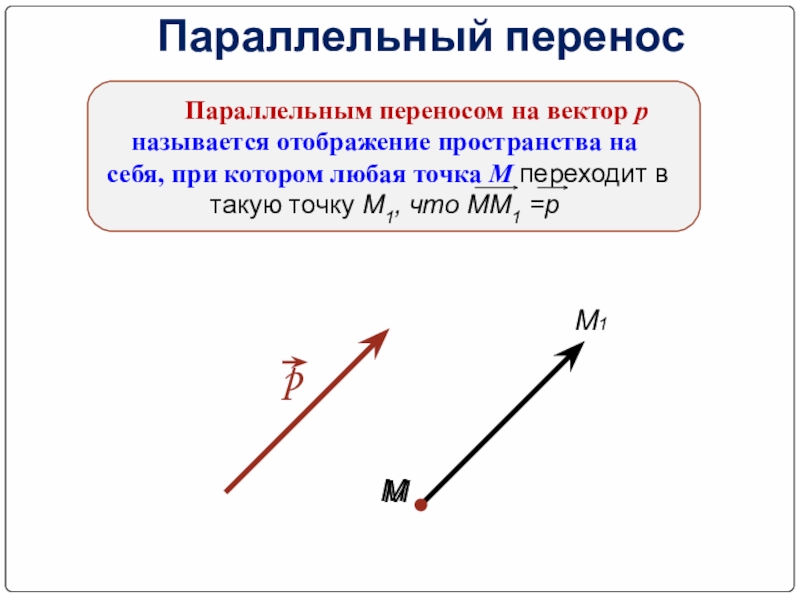
Параллельный перенос
Параллельным переносом на вектор р называется отображение пространства на себя,
при котором любая точка М переходит в такую точку М1, что ММ1 =р
М
М1
М
Слайд 29
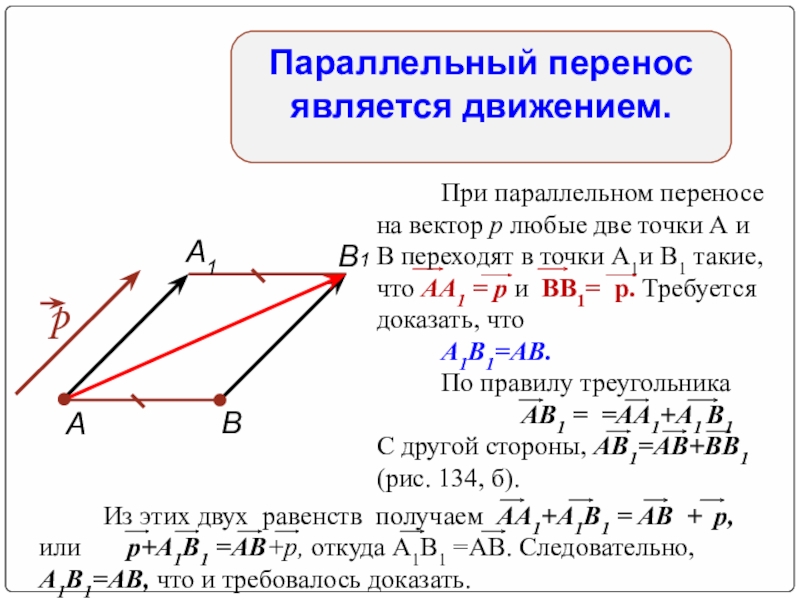
Параллельный перенос является движением.
При параллельном переносе на вектор р любые две
точки А и В переходят в точки А1и В1 такие, что АА1 = р и BB1= р. Требуется доказать, что
А1В1=АВ.
По правилу треугольника
АВ1 = =АА1+А1 В1 C другой стороны, АВ1=АВ+ВВ1 (рис. 134, б).
А1В1=АВ.
По правилу треугольника
АВ1 = =АА1+А1 В1 C другой стороны, АВ1=АВ+ВВ1 (рис. 134, б).
Из этих двух равенств получаем АА1+А1В1 = AВ + p, или р+А1В1 =АВ+p, откуда А1B1 =АВ. Следовательно, А1В1=АВ, что и требовалось доказать.
B1
В
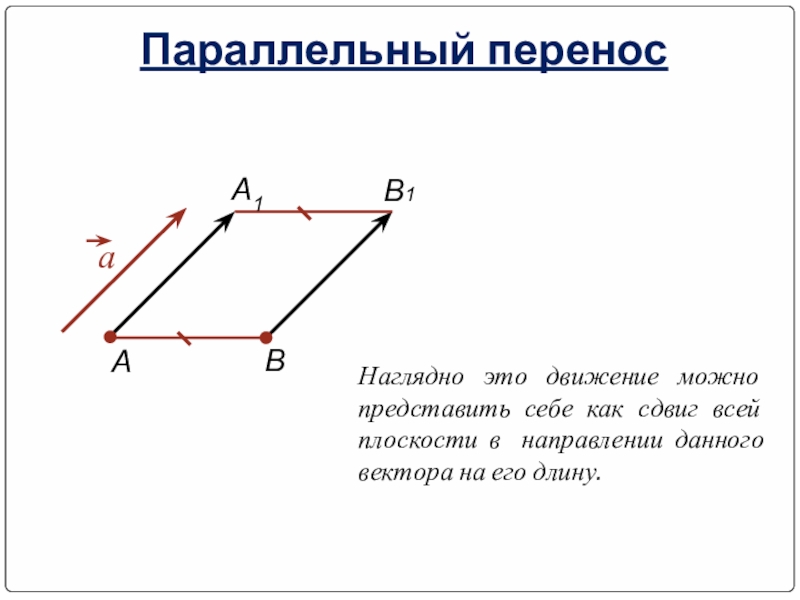
Слайд 30 Параллельный перенос
Наглядно это движение можно представить себе
как сдвиг всей плоскости в направлении данного вектора на его длину.
B1
В
Слайд 34Кувшин. Плоская
симметричная фигура.
Крапива. Винтовая
симметрия.
Звезда. Симметрия
восьмого порядка.
