- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Целые уравнения ( 9 класс)
Содержание
- 1. Презентация по алгебре на тему Целые уравнения ( 9 класс)
- 2. Уравнение, левая и правая часть которого целые выражения называется целым уравнением с одной переменной.
- 3. Решите уравнения:2х-4=0Х2 -5х +6 =0(2х-6)(х+5) = 0Х2 -12х=0Х4-2х2 -3=03х2-2х=2х3 -3У4-у3_16у2+16у=0
- 4. Многочлен, в котором:- нет скобок,- приведены все
- 5. Всякое целое уравнение нужно привести к виду:где Р(х) – многочлен стандартного вида
- 6. Если уравнение с одной переменной записано в
- 7. Чтобы решить какое-либо целое уравнение надо: 1)
- 8. Раскрыть скобки( если есть);Перенести неизвестные слагаемые в
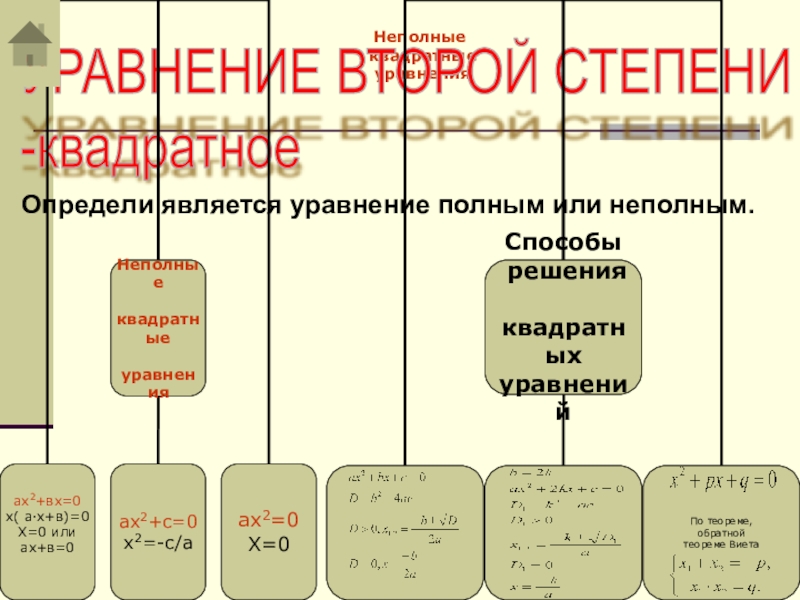
- 9. Неполные квадратные уравненияОпредели является уравнение полным или неполным.УРАВНЕНИЕ ВТОРОЙ СТЕПЕНИ -квадратное
- 10. 1.Вынесение общего множителя.2.Способ группировки.3.Теорема Безу.4.Графический способ.Уравнение третьей степени: способы решения.
- 11. х3-х2 -2х = 0.х( х2 – х-
- 12. СПОСОБ ГРУППИРОВКИ:3х2-2х=2х3 -33х2-2х-2х3 +3=0(3х2-2х3) + ( -2х+3)=0х2(3-2х)
- 13. Если число х=р является корнем многочлена Рп(х),
- 14. х3 + 2х - 3 =0х3= -
- 15. 1.Вынесение общего множителя.2.Способ группировки.3.Теорема Безу.4.Графический способ.5.Биквадратные уравнения.Уравнение четвертой степени: способы решения.
- 16. Уравнение вида ах4 +bх2 +с=0 , где
- 17. 25у4 – 100у2 =025У2(у2 -4) =025У2 =0
- 18. СПОСОБ ГРУППИРОВКИ:У4-у3_16у2+16у=0(у4-у3)+(_16у2+16у)=0у3(у-1)-16у (у-1)=0(у-1)(у3- 16у)=0у(у-1)(у2- 16)=0У=0; у-1=0; у2-
Слайд 1
ТЕМА УРОКА:
"ЦЕЛЫЕ УРАВНЕНИЯ"
ЦЕЛИ УРОКА:
1)научиться различать типы уравнений;
2) научиться решать уравнения
Слайд 2
Уравнение, левая и правая часть которого целые выражения называется целым уравнением
Слайд 3Решите уравнения:
2х-4=0
Х2 -5х +6 =0
(2х-6)(х+5) = 0
Х2 -12х=0
Х4-2х2 -3=0
3х2-2х=2х3 -3
У4-у3_16у2+16у=0
Слайд 4
Многочлен, в котором:
- нет скобок,
- приведены все подобные слагаемые,
- переменные записаны
Называется
МНОГОЧЛЕНОМ СТАНДАРТНОГО ВИДА.
Обозначатся Р(х) .
Слайд 6Если уравнение с одной переменной записано в виде
Р(х)=0,
где Р(х)
то наибольшая степень переменной этого многочлена называют
степенью уравнения.
Слайд 7Чтобы решить какое-либо целое уравнение надо: 1) преобразовать уравнение к виду P(x)=0; 2)
1
2
3
4
Слайд 8
Раскрыть скобки( если есть);
Перенести неизвестные слагаемые в левую часть уравнения, а
Привести подобные слагаемые;
Привести уравнение к виду ах=с;
Найти х:
х=с:а.
УРАВНЕНИЕ ПЕРВОЙ СТЕПЕНИ
-линейное
Слайд 9Неполные
квадратные
уравнения
Определи является уравнение полным или неполным.
УРАВНЕНИЕ ВТОРОЙ СТЕПЕНИ
-квадратное
Слайд 10
1.Вынесение общего множителя.
2.Способ группировки.
3.Теорема Безу.
4.Графический способ.
Уравнение третьей
степени: способы решения.
Слайд 11
х3-х2 -2х = 0.
х( х2 – х- 2) =0.
х=0 или х2
……
х1=2;х2=-1.
ОТВЕТ: -1; 0; 2
Вынесение общего
множителя.
Слайд 12СПОСОБ ГРУППИРОВКИ:
3х2-2х=2х3 -3
3х2-2х-2х3 +3=0
(3х2-2х3) + ( -2х+3)=0
х2(3-2х) + (3 - 2х)=0
(3-2х)(х2
3-2х=0 или х2 + 1=0
-2х=-3 х2 = - 1
Х=1,5 корней
нет
ОТВЕТ: 1,5.
Слайд 13
Если число х=р является корнем многочлена Рп(х), то этот многочлен можно
Дробь корень уравнения а0хп + а1хп-1 +…+ап-1х+ап=0 с целыми коэффициентами, тогда р- делитель свободного члена ап, g- делитель коэффициента а0.
Пример: х3+х2+3х-5=0.
а0=1, делители -5: +1; +5. Подбираем один корень: если х=1, то 13+12+3·1-5=0 верно. Тогда:
х3+х2+3х-5 х-1
х3-х2 х2+2х+5
2х2+3х
2х2-2х
5х-5
5х-5
0 х-1=0 х=1.
Тогда (х-1)(х2+2х+5)=0 или х2+2х+5=0 хєØ х=1
Теорема Безу.
Слайд 14
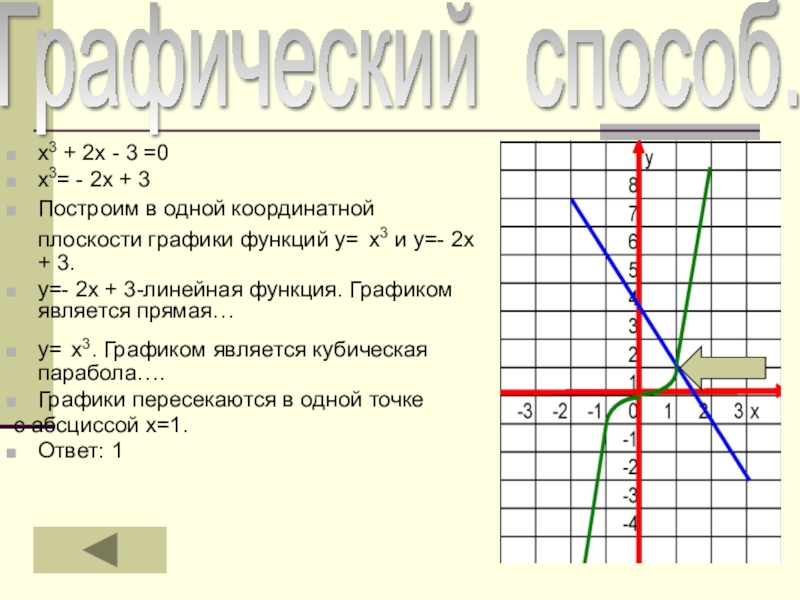
х3 + 2х - 3 =0
х3= - 2х + 3
Построим в
у=- 2х + 3-линейная функция. Графиком является прямая…
у= х3. Графиком является кубическая парабола….
Графики пересекаются в одной точке
с абсциссой х=1.
Ответ: 1
Графический способ.
Слайд 15
1.Вынесение общего множителя.
2.Способ группировки.
3.Теорема Безу.
4.Графический способ.
5.Биквадратные уравнения.
Уравнение четвертой
степени: способы решения.
Слайд 16
Уравнение вида ах4 +bх2 +с=0 ,
где х- независимая переменная, а,
Способ решения- замена х2=t, где t>0.
ПРИМЕР: х4-3х2-4=0.
Пусть х2=t, где t>0, тогда х4=t2. Уравнение примет вид: t2-3t -4=0. Откуда: t1=4, t2= -1.
4>0- верно, -1>0-неверно. Тогда х2=4, х=+2.
Ответ: +2
БИКВАДРАТНЫЕ УРАВНЕНИЯ
Слайд 17
25у4 – 100у2 =0
25У2(у2 -4) =0
25У2 =0 или у2 -4=0
у=0
у=+2
ОТВЕТ: -2;0;2.
Вынесение общего
множителя.
Слайд 18СПОСОБ ГРУППИРОВКИ:
У4-у3_16у2+16у=0
(у4-у3)+(_16у2+16у)=0
у3(у-1)-16у (у-1)=0
(у-1)(у3- 16у)=0
у(у-1)(у2- 16)=0
У=0; у-1=0; у2- 16=0
ОТВЕТ: -4;0;1;4.