- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Решение неравенств с одной переменной (8 класс VII вид)
Содержание
- 1. Презентация по алгебре на тему Решение неравенств с одной переменной (8 класс VII вид)
- 2. Слайд 2
- 3. Устные упражненияЗная, что a < b, поставьте
- 4. Устные упражненияПринадлежит ли отрезку [- 7; -
- 5. Устные упражненияУкажите наибольшее целое число, принадлежащее промежутку:
- 6. Устные упражненияНайди ошибку!x ≥ 7
- 7. Историческая справкаПонятиями неравенства пользовались уже древние греки.
- 8. Историческая справкаСовременные знаки неравенств появились лишь в
- 9. Рассмотрим неравенство 5х –
- 10. Решением неравенства с одной переменной называется значение
- 11. Равносильные неравенства Неравенства, имеющие одни
- 12. При
- 13. Пример 1. Решим неравенство
- 14. Алгоритм решения неравенств первой степени
- 15. Слайд 15
- 16. Алгоритм решения неравенств первой степени
- 17. 5х ≤ 15,
- 18. Слайд 18
- 19. А теперь ребята встали!Быстро руки вверх подняли,В
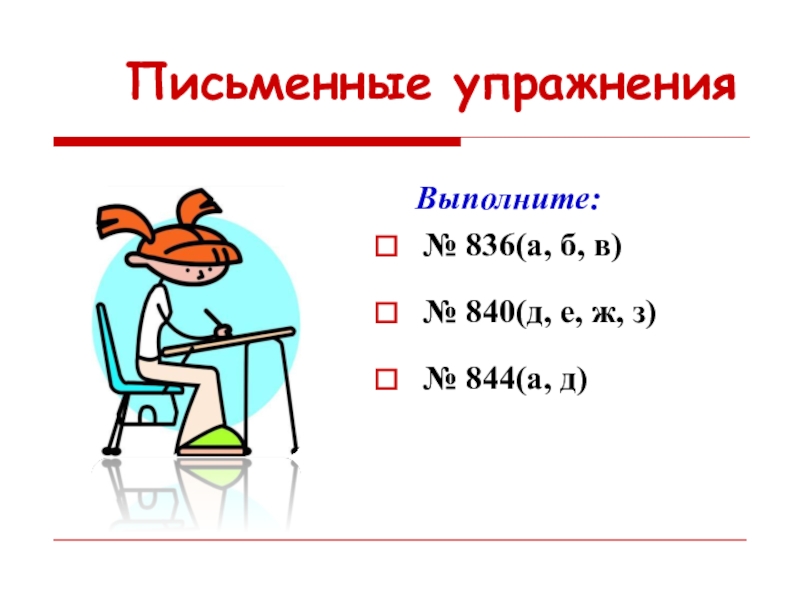
- 20. Письменные упражнения Выполните:№ 836(а, б, в) № 840(д, е, ж, з)№ 844(а, д)
- 21. урок был интересен и полезен для меня,
- 22. Домашнее заданиеИзучить п.34(выучить определения, свойства и алгоритм
- 23. Спасибо за внимание! Урок окончен!
Слайд 2
ввести понятия «решение неравенства», «равносильные неравенства»;
познакомиться со свойствами равносильности неравенств;
рассмотреть решение линейных неравенств вида ах > b, ax < b;
научиться решать неравенства с одной переменной, опираясь на свойства
равносильности.
Слайд 3Устные упражнения
Зная, что a < b, поставьте соответствующий знак < или
1) -5а □ - 5b
2) 5а □ 5b
3) a – 4 □ b – 4
4) b + 3 □ a +3
Слайд 5Устные упражнения
Укажите наибольшее целое число, принадлежащее промежутку:
[-1; 4]
(- ∞; 3)
(2; + ∞)
4
2
не существует
Слайд 7Историческая справка
Понятиями неравенства пользовались уже древние греки.
Например, Архимед (III в.
Ряд неравенств приводит в своём трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух чисел не больше их среднего арифметического и не меньше их среднего гармонического.
Слайд 8Историческая справка
Современные знаки неравенств появились лишь в XVII— XVIII вв.
В 1631
Символы ≤ и ≥ были введены в 1734 году французским математиком Пьером Буге́ром.
Слайд 9
Рассмотрим неравенство 5х – 11 > 3
при х = 4
при х = 2 5 • 2 – 11 > 3, - 1 > 3 – неверно;
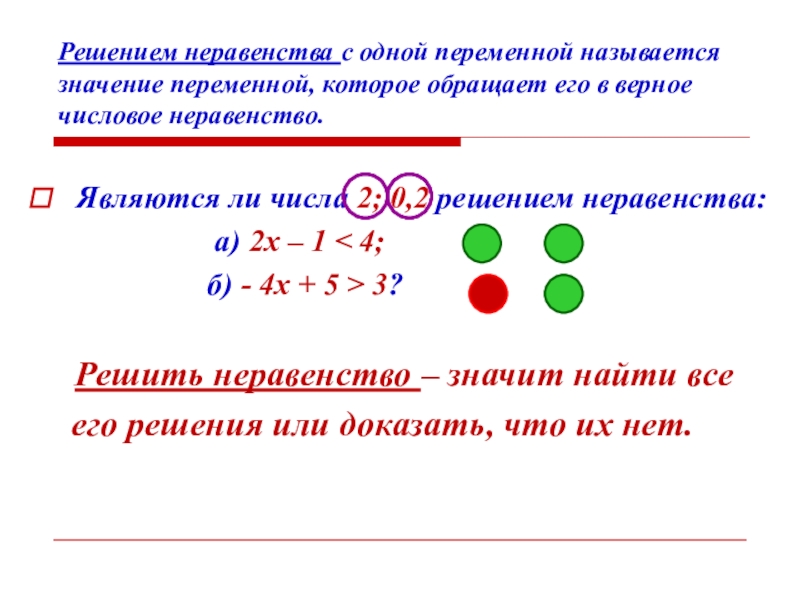
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Слайд 10Решением неравенства с одной переменной называется значение переменной, которое обращает его
Являются ли числа 2; 0,2 решением неравенства:
а) 2х – 1 < 4;
б) - 4х + 5 > 3?
Решить неравенство – значит найти все
его решения или доказать, что их нет.
Слайд 11Равносильные неравенства
Неравенства, имеющие одни и те же решения,
2х – 6 > 0 и равносильны х > 3
х2 + 4 ≤ 0 и |х| + 3 < 0 равносильны нет решений
3х – 6 ≥ 0 и 2х > 8 неравносильны
х ≥ 2 х > 4
Слайд 12
При решении неравенств используются следующие свойства:
Если из
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Слайд 13Пример 1. Решим неравенство
Раскроем скобки, подчеркнем подобные слагаемые:
Сгруппируем в левой части слагаемые с переменной, а
в правой - без переменной:
Приведём подобные слагаемые:
Разделим обе части неравенства на положительное число 3,
сохраняя при этом знак неравенства:
6х – 3 > 2х+4+1х + 5
6х–2х–1х > 3 + 4 + 5
3х > 12
х > 12:3
х > 4
4 х
Ответ: (4; + ∞)
Слайд 14 Алгоритм решения неравенств первой степени с одной переменной.
Раскрыть скобки
Сгруппировать слагаемые с переменной в левой части неравенства, а без переменной – в правой части, при переносе меняя знаки.
Привести подобные слагаемые.
Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю.
Изобразить множество решений неравенства на координатной прямой.
Записать ответ в виде числового промежутка.
Слайд 15
Знак изменится, когда неравенств обе части
Делить на с минусом число
1) – 2х < 4
2) – 2х > 6
3) – 2х ≤ 6
Решите неравенство:
4) – х < 12
5) – х ≤ 0
6) – х ≥ 4
х > - 2
х < - 3
х ≥ - 3
х > - 12
х ≥ 0
х ≤ - 4
Слайд 16 Алгоритм решения неравенств первой степени с одной переменной.
Раскрыть скобки
Сгруппировать слагаемые с переменной в левой части неравенства, а без переменной – в правой части, при переносе меняя знаки.
Привести подобные слагаемые.
Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю:
если коэффициент > 0 знак неравенства не поменяется,
если коэффициент < 0 знак изменится на противоположный.
Изобразить множество решений неравенства на координатной прямой.
Записать ответ в виде числового промежутка.
Слайд 17 5х ≤ 15, 3х > 12,
Решения неравенств ах > b или ах < b при а = 0.
Пример 1. 0 • х < 48
Пример 2. 0 • х < - 7
Линейное неравенство вида 0 • х < b или 0 • х > b, а значит и соответствующее ему исходное неравенство, либо не имеет решений, либо его решением является любое число.
Неравенства вида ах > b или ах < b, где а и b –
некоторые числа, называют линейными неравенствами
с одной переменной.
Ответ: х – любое число.
Ответ: нет решений.
Слайд 18
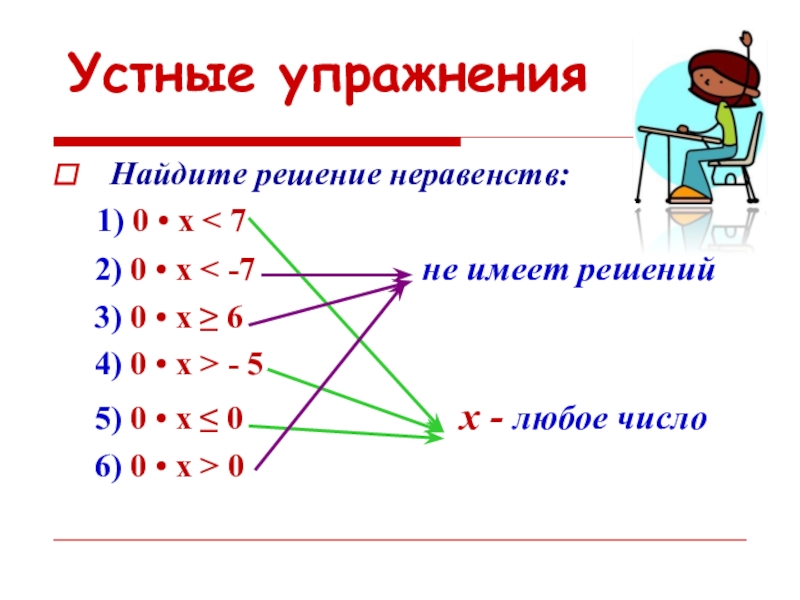
Найдите решение неравенств:
1) 0 • х < 7
2) 0 • x < -7 не имеет решений
3) 0 • х ≥ 6
4) 0 • х > - 5
5) 0 • х ≤ 0 х - любое число
6) 0 • x > 0
Слайд 19А теперь ребята встали!
Быстро руки вверх подняли,
В стороны, вперед, наклон.
Выпрямились, повернулись
Тихо сели – вновь за дело.
Физкульт минут ка
Слайд 21
урок был интересен и полезен для меня,
я хорошо работал,
всё
мне было достаточно комфортно
урок был интересен и в определенной степени полезен для меня
я принимал участие,
но понимал не все задания,
с домашним заданием, думаю, справлюсь.
пользы от урока я получил мало,
я не очень понимаю, о чем идет речь,
мне это не понятно, не нужно, не интересно,
домашнее задание я не смогу сделать.
Слайд 22Домашнее задание
Изучить п.34(выучить определения, свойства и алгоритм решения).
Выполнить
№
№ 836(д – к);
№ 841(д – з)



![Презентация по алгебре на тему Решение неравенств с одной переменной (8 класс VII вид) Устные упражненияПринадлежит ли отрезку [- 7; - 4] число: - 10 Устные упражненияПринадлежит ли отрезку [- 7; - 4] число: - 10 - 6,5 - 4 - 3,1](/img/thumbs/1a1cadf46eeb9d816142551ce81003a3-800x.jpg)
![Презентация по алгебре на тему Решение неравенств с одной переменной (8 класс VII вид) Устные упражненияУкажите наибольшее целое число, принадлежащее промежутку: [-1; 4] Устные упражненияУкажите наибольшее целое число, принадлежащее промежутку: [-1; 4] (- ∞; 3)](/img/tmb/8/718231/223cbf96fba44b87ecfc70fd351f6f86-800x.jpg)