- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Прогрессии (9 класс)
Содержание
- 1. Презентация по алгебре на тему Прогрессии (9 класс)
- 2. ПРОГРЕССИИГеометрическая прогрессияЧисловая последовательностьАрифметическая прогрессия
- 3. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬПоследовательность целых чисел: ...-3; -2; -1;
- 4. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ а1 ,а2 ,а3 ,а4,….аn
- 5. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬПоследовательность натуральных чисел:1; 2; 3; 4;
- 6. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬПоследовательность чётных чисел: 2; 4; 6;………….(2n-2);
- 7. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬПоследовательность квадратов натуральных чисел: 1; 4;
- 8. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬФормула n-го члена позволяет решать различные
- 9. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬб) определить порядковый номер данного члена
- 10. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬИногда последовательность задают формулой, позволяющей вычислить
- 11. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬПример. Последовательность задана рекурентной формулой bn+1=
- 12. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ1 +2 = 35 + 2
- 13. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Арифметической прогрессией называется числовая последовательность
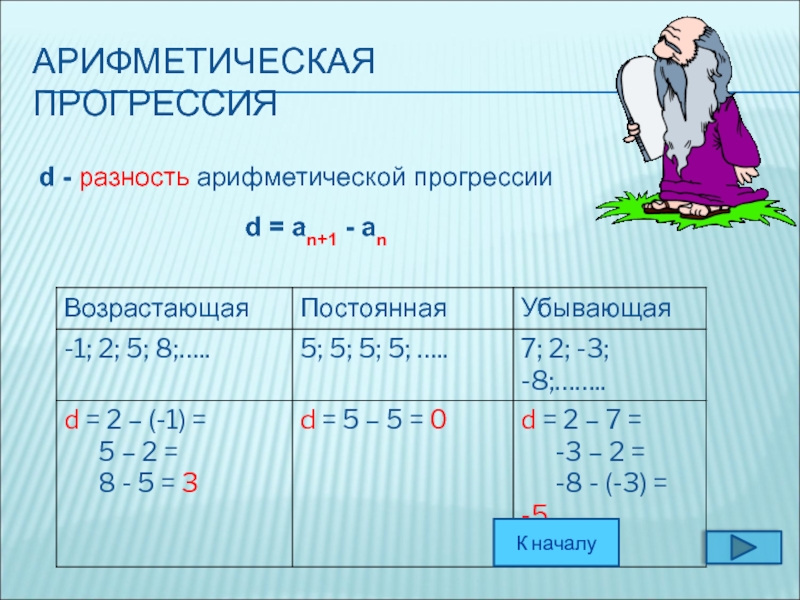
- 14. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯd - разность арифметической прогрессииd = an+1 - an К началу
- 15. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯСвойство: Каждый член арифметической прогрессии, начиная
- 16. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЗадача.
- 17. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЗадача.Найти
- 18. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЕсли
- 19. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЗадача.Найти
- 20. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЗадача.Найти
- 21. СУММА N ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯЗадача.Найти
- 22. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Найти
- 23. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ последовательность чисел, в которой каждый
- 24. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- 25. К началу
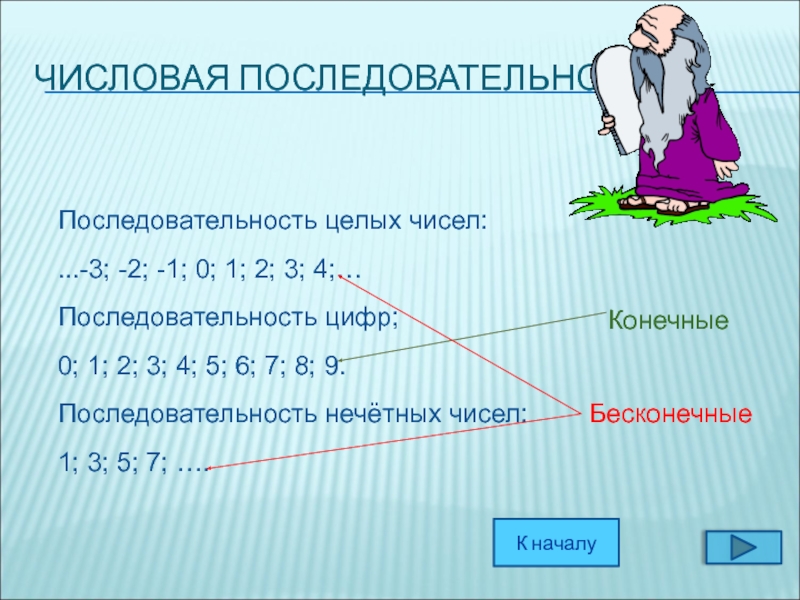
Слайд 3ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Последовательность целых чисел:
...-3; -2; -1; 0; 1; 2; 3;
Последовательность цифр;
0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Последовательность нечётных чисел:
1; 3; 5; 7; ….
Конечные
Бесконечные
К началу
Слайд 4ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
а1 ,а2 ,а3 ,а4,….аn -
числовая последовательность, где
а1 – первый член последовательности;
а2 – второй член последовательности;
а3 – третий член последовательности;
а4 – четвёртый член последовательности;
…
аn – n-ый член последовательности.
1; 2; 3; 4;……;n – порядковые номера
К началу
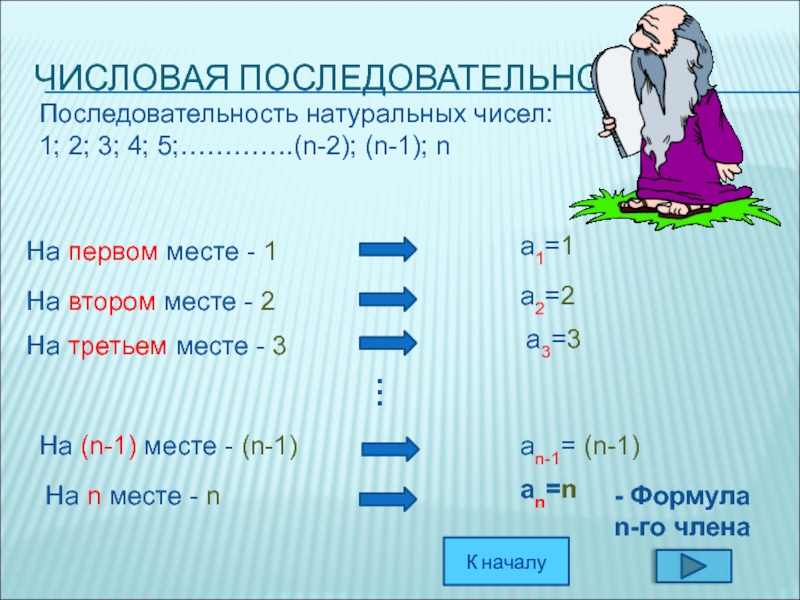
Слайд 5ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Последовательность натуральных чисел:
1; 2; 3; 4; 5;………….(n-2); (n-1); n
На первом
а1=1
На третьем месте - 3
На втором месте - 2
На (n-1) месте - (n-1)
На n месте - n
а2=2
аn=n
аn-1= (n-1)
а3=3
…
- Формула
n-го члена
К началу
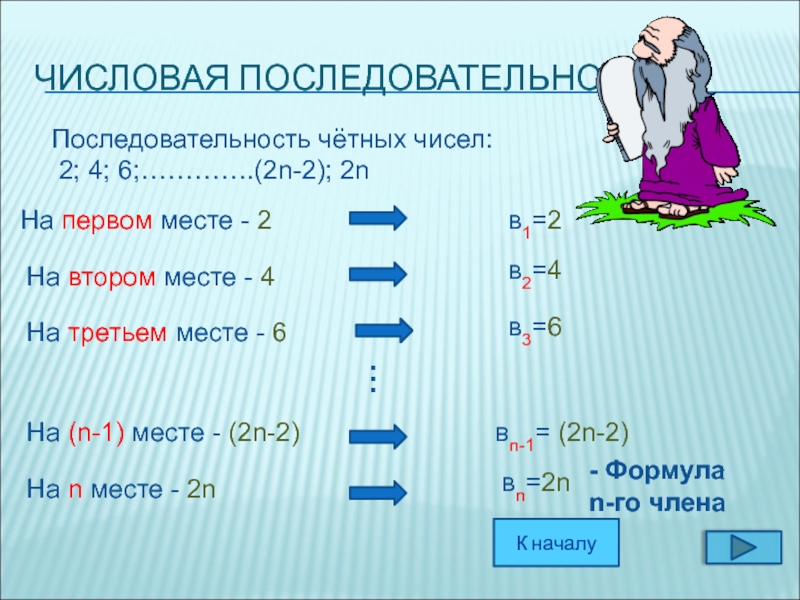
Слайд 6ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Последовательность чётных чисел:
2; 4; 6;………….(2n-2); 2n
На первом месте -
в1=2
На третьем месте - 6
На втором месте - 4
На (n-1) месте - (2n-2)
На n месте - 2n
в2=4
вn=2n
вn-1= (2n-2)
в3=6
…
- Формула
n-го члена
К началу
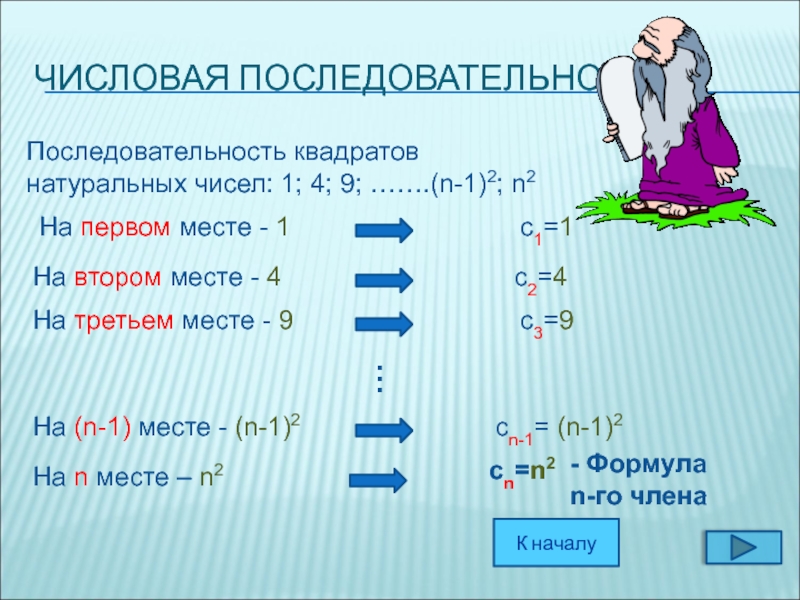
Слайд 7ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Последовательность квадратов натуральных чисел: 1; 4; 9; …….(n-1)2; n2
На первом
с1=1
На третьем месте - 9
На втором месте - 4
На (n-1) месте - (n-1)2
На n месте – n2
с2=4
сn=n2
сn-1= (n-1)2
с3=9
…
- Формула
n-го члена
К началу
Слайд 8ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Формула n-го члена позволяет решать
различные задачи:
а)вычислить любой член данной
Пример
Числовая последовательность задана формулой уn=n(n-2).
Вычислить сотый член этой последовательности.
Решение: так как сотый член последовательности у100, то n=100. у100=100(100-2)=9800
К началу
Слайд 9ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
б) определить порядковый номер данного
члена последовательности
Пример
Числовая последовательность
Найти номер члена последовательности, равного:
1) 43; 2) 50.
Решение: 1) пусть 43 стоит на k-ом месте, тогда 2k+3=43;
2k=40;
k=20,
т.к. 20-натуральное число, то 43 стоит на 20 месте
Решение: 2) пусть 50 стоит на m-ом месте, тогда 2m+3=50;
2m=47;
m=23,5,
т.к.23,5 не является натуральным числом, то в последовательности нет числа 50.
К началу
Слайд 10ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Иногда последовательность задают формулой, позволяющей вычислить (n +1)-й член последовательности
К началу
Слайд 11ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Пример.
Последовательность задана рекурентной формулой bn+1= bn + bn-1 и
Вычислить пятый член этой последовательности.
Решение: так как b3= b2 +b1, то b3= 3+1=4;
так как b4= b3 +b2, то b4= 4+3=7;
так как b5= b4 +b3, то b5= 7+4=11;
К началу
Слайд 12АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
1 +2 = 3
5 + 2 = 7;
1
3 +2 =
+
+
+
1; 3; 5; 7;…последовательность, каждый член которой,
начиная со второго, равен предыдущему сложенному
с одним и тем же числом называют
Арифметической прогрессией
К началу
Слайд 13АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Арифметической прогрессией называется
числовая последовательность a1, a2, a3, ...
если для всех натуральных n выполняется
равенство an+1 = an + d, где d - некоторое число.
0 + 2 = 2
2 +2 = 4
-2;
-2 + 2=0;
0;
2;
4;
…..
К началу
Слайд 15АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
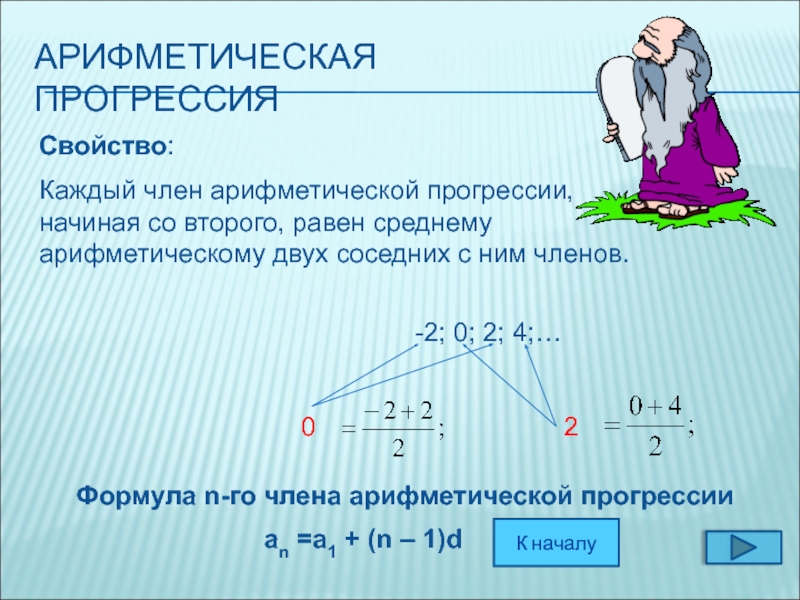
Свойство:
Каждый член арифметической прогрессии, начиная со второго, равен среднему
Формула n-го члена арифметической прогрессии
an =a1 + (n – 1)d
0
2
-2; 0; 2; 4;…
К началу
Слайд 16СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Задача.
Найти сумму всех натуральных чисел
S= 1 + 2 + 3 +…+99+100
S=99+98+97+…+ 2 + 1
Сложим почленно: 2S =(1+99)+(2+98)+(3+97)+…+(99+2)+(100+1)
2S=101+101+101+…+101+101
100 слагаемых
2S=101*100
S=101*50=5050
К началу
Слайд 17СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Задача.
Найти сумму n первых членов
арифметической прогрессии
Сложим почленно: S=a1 + a2 +… + an-1 + an
S=an + an-1 +…a2 + +a1
2S=(a1 + an)+ (a1 + an)+…+ (a1 + an)+ (a1 + an)
2S=(a1 + an)+ (a2 + an-1)+… + (an-1 + a1) +(an+ a2)
n слагаемых
2S= (a1 + an)*n
К началу
Слайд 18СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Если заменить an = a1 +
К началу
Слайд 19СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Задача.
Найти сумму 50 первых членов
арифметической прогрессии,
Решение:
К началу
Слайд 20СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Задача.
Найти сумму 12 первых членов
арифметической прогрессии,
Решение:
К началу
Слайд 21СУММА N ПЕРВЫХ ЧЛЕНОВ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Задача.
Найти сумму 50 первых членов
арифметической прогрессии,
Решение:
К началу
Слайд 22
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Найти первый член прогрессии и её разность,
если
a1 + a5= 24; a2 * a3= 60;
Решение: a1 + a5= 24;
a2 * a3= 60;
a1 + a1+4d = 24;
(a1+d) *(a1+2d) = 60;
2a1 +4d = 24;
(a1+d) *(a1+2d)= 60;
a1 = 12 - 2d;
(12 - 2d+d) *(12 - 2d+2d)= 60;
a1 = 12 - 2d;
(12 - d) *12 = 60;
a1 = 12 - 2d;
12 - d = 60:12;
a1 = 12 - 2d;
12 - d = 5;
a1 = 12 - 2d;
d = 7;
a1 = 12 – 2*7;
d = 7;
a1 = – 2;
d = 7;
К началу
Слайд 23ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
последовательность чисел, в которой каждый член,
начиная со второго, равен
число, называют ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИЕЙ
Задача. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Запишите колонию, рожденную одной бактерией за 5 мин.
1; 2; 4; 8; 16
К началу
Слайд 24ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
1см
Рассмотрим равносторонний треугольник со стороной 1 см. Построим треугольник, вершинами которого являются середины сторон данного треугольника. Продолжая аналогичные построения, получим последовательность длин сторон треугольников:
Числовая последовательность b1, b2, b3,… bn,… называется геометрической прогрессией, если для всех натуральных n выполняется равенство bn+1= bnq, где bn≠0, q- некоторое число, не равное нулю.
К началу