- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Квадратичная функция (8 класс)
Содержание
- 1. Презентация по алгебре на тему Квадратичная функция (8 класс)
- 2. Проблема:Ученики говорят: «Изучать функции не очень интересно. Да и где они нам в жизни понадобятся!»
- 3. Гипотеза:ученики плохо знают свойства функций не видят области применения скучных математических формул
- 4. Задачи исследования:изучить свойства параболыизучить, какие процессы выражаются графиком - параболойвыявить области применения параболы
- 5. Содержание работы:Определение параболыСвойства параболыОбласти применения параболы
- 6. Конические сеченияКонические сечения были открыты в Древней
- 7. Параболаэто сечение конуса плоскостью, параллельной его образующей.
- 8. Параболаэто геометрическое место точек плоскости, находящихся на
- 9. Свойства параболыИмеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
- 10. Геометрические свойства параболыПарабола — кривая второго порядка.Все параболы
- 11. Парабола является антиподерой прямой, т.е. можно рассматривать, как огибающую семейства прямыхГеометрические свойства параболы
- 12. Оптическое свойство параболыПучок лучей, параллельных оси параболы,
- 13. Архимед (287 до н.э. — 212 до н.э.)
- 14. Парабола и историяСогласно известной исторической легенде, Архимед
- 15. Зеркало Архимеда в наше времяПараболические зеркала, улавливающие
- 16. Парабола и олимпиада
- 17. Применение свойств параболы в повседневной жизниСвойство параболы
- 18. Физическое свойство параболыПри вращении сосуда с жидкостью
- 19. Парабола и космосТраектории некоторых космических тел, проходящих
- 20. Применение свойств параболы в самолетостроенииДля создания невесомости
- 21. Баллистика - наука о полёте тел, основанная
- 22. Парабола в повседневной жизниТраектории прыжков
- 23. Парабола в архитектуреПочти все силы в опорах
- 24. Парабола в повседневной жизниСтруя воды, направленная в воздух, летит по параболе
- 25. Вывод:Функции скучны только для тех, кто их не изучает.Математическими формулами описаны все процессы в нашей жизни
- 26. Список литературыЖурнал «Квант», №2, 1971 г.;Пидоу Д.,
- 27. Источники информацииhttp://ru.wikipedia.org/wiki/%CF%E0%F0%E0%E1%EE%EB%E0http://ru.wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%E8%F7%ED%E0%FF_%F4%F3%ED%EA%F6%E8%FF#.D0.9E.D0.B1.D0.BE.D0.B1.D1.89.D0.B5.D0.BD.D0.B8.D0.B5http://ru.convdocs.org/docs/index-2161.htmlhttp://www.etudes.ru/
Проблема:Ученики говорят: «Изучать функции не очень интересно. Да и где они нам в жизни понадобятся!»
Слайд 2Проблема:
Ученики говорят: «Изучать функции не очень интересно. Да и где они
нам в жизни понадобятся!»
Слайд 3Гипотеза:
ученики плохо знают свойства функций
не видят области применения скучных математических
формул
Слайд 4Задачи исследования:
изучить свойства параболы
изучить, какие процессы выражаются графиком - параболой
выявить области
применения параболы
Слайд 6Конические сечения
Конические сечения были открыты в Древней Греции и описаны Аполлонием
Пергским (ок. 260 — ок. 170 гг. до н. э.). Коническими сечениями называют эллипс, гиперболу и параболу, так как эти кривые можно получить на поверхности круглого конуса в пересечении плоскостью, не проходящей через вершину конуса.
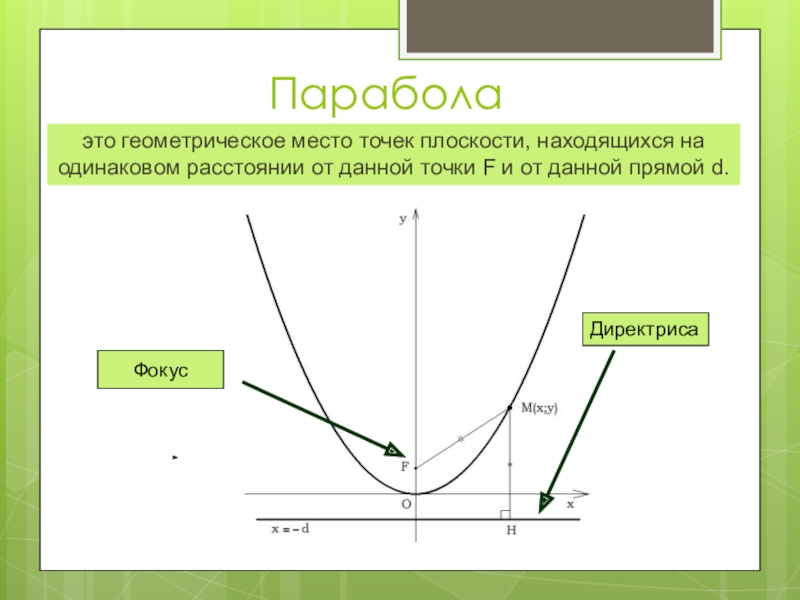
Слайд 8Парабола
это геометрическое место точек плоскости, находящихся на одинаковом расстоянии от данной
точки F и от данной прямой d.
Фокус
Директриса
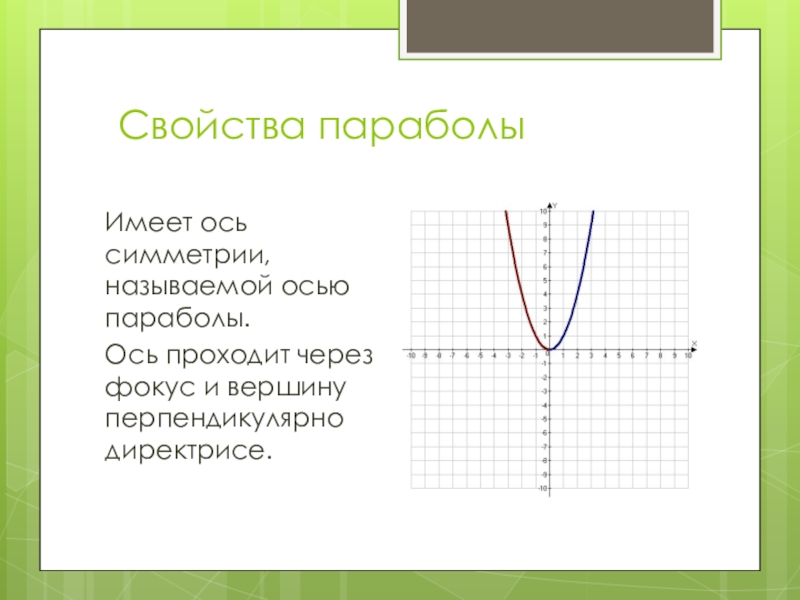
Слайд 9Свойства параболы
Имеет ось симметрии, называемой осью параболы.
Ось проходит через фокус
и вершину перпендикулярно директрисе.
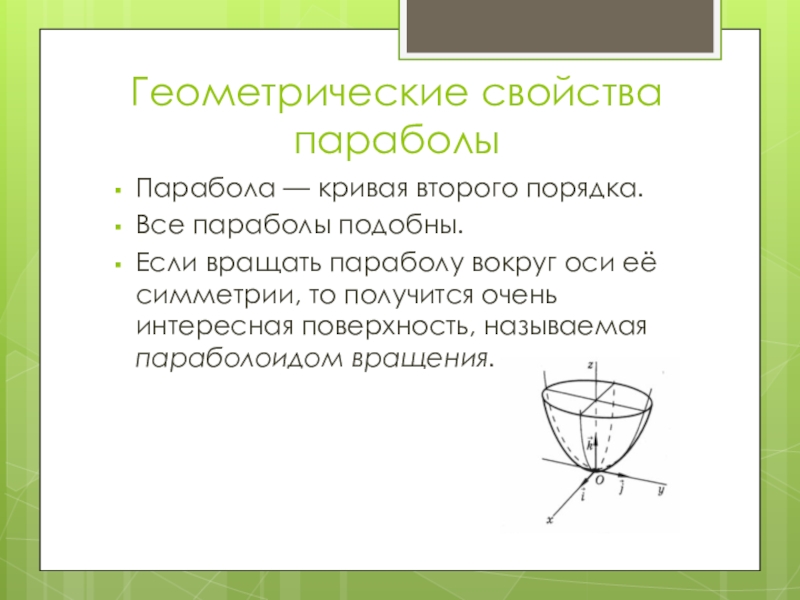
Слайд 10Геометрические свойства параболы
Парабола — кривая второго порядка.
Все параболы подобны.
Если вращать параболу вокруг
оси её симметрии, то получится очень интересная поверхность, называемая параболоидом вращения.
Слайд 11Парабола является антиподерой прямой, т.е. можно рассматривать, как огибающую семейства прямых
Геометрические
свойства параболы
Слайд 12Оптическое свойство параболы
Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается
в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
Слайд 14Парабола и история
Согласно известной исторической легенде, Архимед почти полностью сжег флот
римского полководца Марка Марцелла, при нападении на родной город Архимеда (212 до н.э.), используя медные параболические зеркала
Слайд 15Зеркало Архимеда в наше время
Параболические зеркала, улавливающие солнечный свет, используются для
разогревания продуктов, выработки электричества, в металлообработке и при получении водорода.
Самый крупный из таких объектов расположен в деревеньке Одейо во французских Пиренеях: 8-этажный массив включает 10 тыс. небольших зеркал, вместе создающих в фокальной точке температуру в 3 тыс. градусов по Цельсию.
Самый крупный из таких объектов расположен в деревеньке Одейо во французских Пиренеях: 8-этажный массив включает 10 тыс. небольших зеркал, вместе создающих в фокальной точке температуру в 3 тыс. градусов по Цельсию.
Слайд 17Применение свойств параболы в повседневной жизни
Свойство параболы фокусировать пучок лучей, параллельных
оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанциях и в других областях.
Слайд 18Физическое свойство параболы
При вращении сосуда с жидкостью вокруг вертикальной оси поверхность
жидкости в сосуде и вертикальная плоскость пересекаются по параболе.
Слайд 19Парабола и космос
Траектории некоторых космических тел, проходящих вблизи звезды или другого
массивного объекта на достаточно большой скорости имеют форму параболы. Эти тела вследствие своей большой скорости не захватываются гравитационных полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей.
Слайд 20Применение свойств параболы в самолетостроении
Для создания невесомости в земных условиях проводятся
полёты самолётов по параболической траектории, так называемой параболе Кеплера.
Слайд 21Баллистика - наука о полёте тел, основанная на физике и математике.
Во всех случаях снаряд летит по параболе.
Слайд 23Парабола в архитектуре
Почти все силы в опорах направлены вертикально вниз и
стабилизируются за счёт тросов, поэтому опоры могут быть очень тонкими.
Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе.
Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе.
Висячие мосты
Слайд 25Вывод:
Функции скучны только для тех, кто их не изучает.
Математическими формулами описаны
все процессы в нашей жизни
Слайд 26Список литературы
Журнал «Квант», №2, 1971 г.;
Пидоу Д., Геометрия и искусство, «Мир»,
М., 1979 г.;
Сергеев И.Н. и др. Зарубежные математические олимпиады, «Наука», М., 1987 г.
Сергеев И.Н. и др. Зарубежные математические олимпиады, «Наука», М., 1987 г.