Презентация, доклад по алгебре 8 класс Квадратные уравнения

Европе 13-17 в.в.
Определение.
Неполные кв. уравнения.
Полное кв. уравнение.
Теорема Виета.
Теорема, обратная теореме Виета.
Кв. уравнения с комплексными переменными.
Решение кв. уравнений с помощью графиков.
Разложение кв. трехчлена на множители.
Применение кв. уравнений.

Главное меню

Необходимость решать уравнения  не только первой, но и второй степени ёщё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их  клинописных текстах  встречаются, кроме неполных, и такие, например, полные квадратные уравнения:





Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

 

Кв. уравнения в Индии. Главное меню

Задачи на квадратные уравнения встречаются уже в 499 г. 
В Древней Индии были распространены публичные соревнования в решении трудных задач.
В одной из старинных индийских книг говорится по поводу таких соревнований следующее: "Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи.
Задача знаменитого индийского математика  Бхаскары: 
Обезьянок резвых стая  Всласть  поевши, развлекаясь.  Их в квадрате часть восьмая  На поляне забавлялась.  А 12 по лианам.....  Стали прыгать, повисая.  Сколько было обезьянок,  Ты  скажи мне, в этой стае?

в Европе были впервые  изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.  
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2+вх+с=0 , было сформулировано в Европе лишь в 1544 г. Штифелем.       
Вывод формулы решения квадратного уравнения  в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Определение Главное меню

Уравнение вида ax2+bx+c=0, где a, b, c - действительные числа, причем a не равно 0, называют квадратным уравнением.
Если a = 1 , то    квадратное  уравнение    называют приведенным;
 если a ¹ 1, то    неприведенным .  Числа a, b, c носят следующие названия:a -первый коэффициент, 
b - второй коэффициент, c - свободный член.
Корни уравнения ax2+bx+c=0 находят по формуле
   Выражение D = b2- 4ac называют дискриминантом квадратного уравнения.
Если D < 0, то уравнение не имеет действительных корней;
 если D = 0, то уравнение имеет один действительный корень;
 если D > 0, то уравнение имеет два действительных корня.  
В случае, когда D = 0, иногда говорят, что квадратное уравнение  имеет два одинаковых корня.
 
 Используя обозначение D = b2- 4ac, можно переписать формулу в виде


Если b = 2k, то формула  принимает вид:


Итак,


где k = b / 2. Последняя формула особенно удобна в тех случаях, когда b / 2 - целое число, т.е. коэффициент, b - четное число.

Неполные кв. уравнения Главное меню

Если в квадратном уравнении ax2+bx+c=0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.  
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения - проще решить уравнение методом разложения его левой части на множители.
Способы решения неполных квадратных уравнений:
1)  c = 0 , то уравнение примет вид  
ax2+bx=0.                  
 x( ax + b ) = 0 ,
 x = 0 или ax + b = 0 ,        
x = -b : a .
2) b = 0, то уравнение
примет вид
ax2 + c = 0 ,
x2 = -c : a ,

x1 = или x2 = -

3) b = 0 и c = 0 , то уравнение примет вид
ax2 = 0,
x =0.  

квадратное уравнение Главное меню

Если в квадратном уравнении второй коэффициент и свободный член не равны нулю, то такое уравнение называют полным квадратным уравнением.

Теорема Виета Главное меню

Теорема. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Доказательство. Рассмотрим приведённое квадратное уравнение. Обозначим второй коэффициент буквой p, а свободный член - буквой q:


Дискриминант этого уравнения D равен

Пусть D>0 .Тогда это уравнение имеет два корня:


и

Найдём сумму и произведение корней:

Главное меню

Теорема. Если числа m и n таковы, что их сумма равна –p, а произведение

равно q, то эти числа являются корнями уравнения

Доказательство. По условию m+n=-p,а mn=q. Значит, уравнение
можно записать в виде
Подставив вместо x число m, получим:


Значит, число m является корнем уравнения.
Аналогично можно показать, что число n так же является корнем уравнения:


По праву в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни и дробь уж готова:
В числителе С, в знаменателе А,
А сумма корней тоже дроби равна
Хоть с минусом дробь эта, что за беда-
В числителе b, в знаменателе a.

Главное меню

Сначала рассмотрим простейшее кв. уравнение

где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:



На множестве комплексных чисел это уравнение всегда имеет корень.
Задача1. Найти комплексные корни если а=-1
1) Т.к. =-1, то это уравнение можно записать в виде , или .
Отсюда, раскладывая левую часть на множители, получаем
Ответ:

1)Имеет один корень z=0, если а=0;
2)Имеет два действительных корня

, если а>0.
3)Не имеет действительных корней, если a<0.

уравнений с помощью графиков. Главное меню

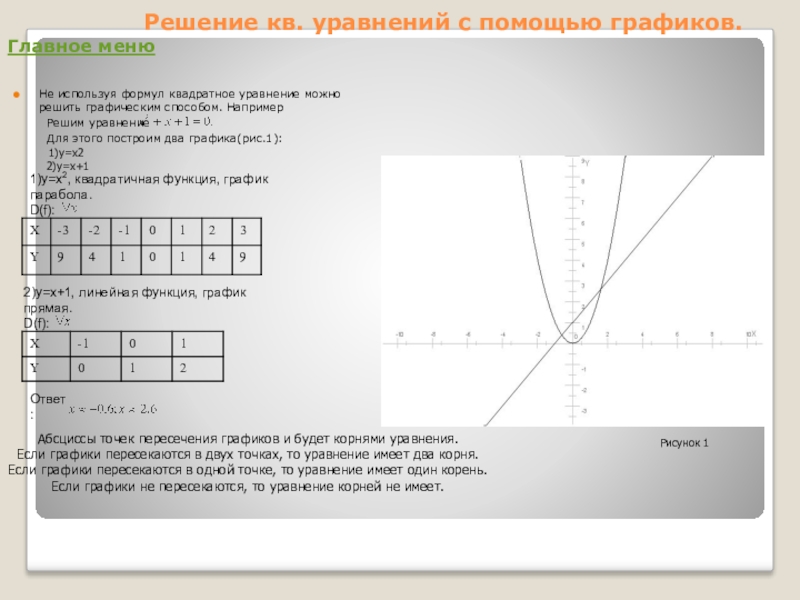
Не используя формул квадратное уравнение можно решить графическим способом. Например
Решим уравнение
Для этого построим два графика(рис.1):

1)y=x2
2)y=x+1

1)y=x2, квадратичная функция, график парабола.
D(f):

2)y=x+1, линейная функция, график прямая.
D(f):

Рисунок 1

Ответ:

Абсциссы точек пересечения графиков и будет корнями уравнения.
Если графики пересекаются в двух точках, то уравнение имеет два корня.
Если графики пересекаются в одной точке, то уравнение имеет один корень.
Если графики не пересекаются, то уравнение корней не имеет.

множители Главное меню

Многочлен вида ax2+bx+c, где a,b,c - некоторые числа, x переменная, называется квадратным трёхчленом.
Пример 3x2+7x+9
Квадратный трехчлен разлагается на множители , где и корни трехчлена.
Дано: - квадратный трехчлен; и -корни его
Доказать:
Доказательство:

по теореме Виета следует,

Применение кв. уравнений Главное меню

Решение квадратных уравнений широко применяется в других разделах математики: в разложении квадратного трехчлена, в исследовании квадратичной функции, в решении уравнений высших степеней, в решении текстовых задач и задач по геометрии.
       
Некоторые уравнения высших степеней можно решить, сведя их к квадратному.

1) Иногда левую часть уравнения легко разложить на множители, из  которых каждый - многочлен не выше 2-ой степени. Тогда приравнивая каждый многочлен к нулю, решаем полученные уравнения.
ПРИМЕР:






2)  Если уравнение имеет вид ax2n+bxn+c= 0, его можно свести к квадратному, введя новую переменную   t = x.
ПРИМЕР: 







3)  В геометрии:
Гипотенуза прямоугольного треугольника равна 10. Найти катеты, если один из них на 2 см. больше другого.
РЕШЕНИЕ: по теореме  Пифагора  a2+ b2= c2
Пусть х см.-1 катет, тогда (х+2) см.-2 катет.     
Составим уравнение:   x2+ (x+2)2= 102
Пифагор