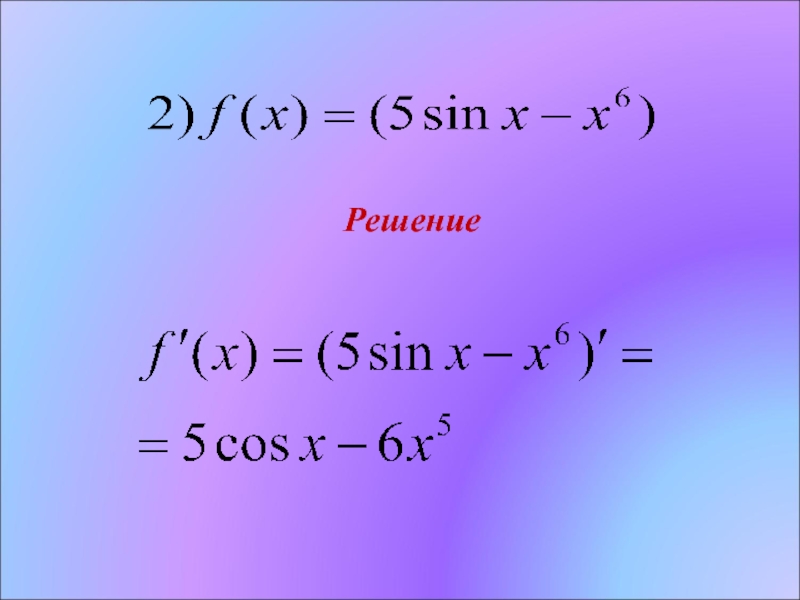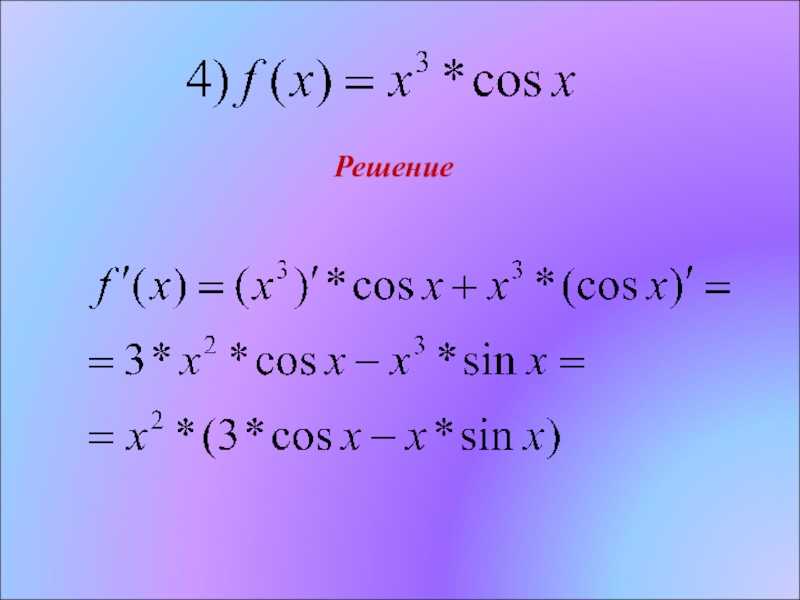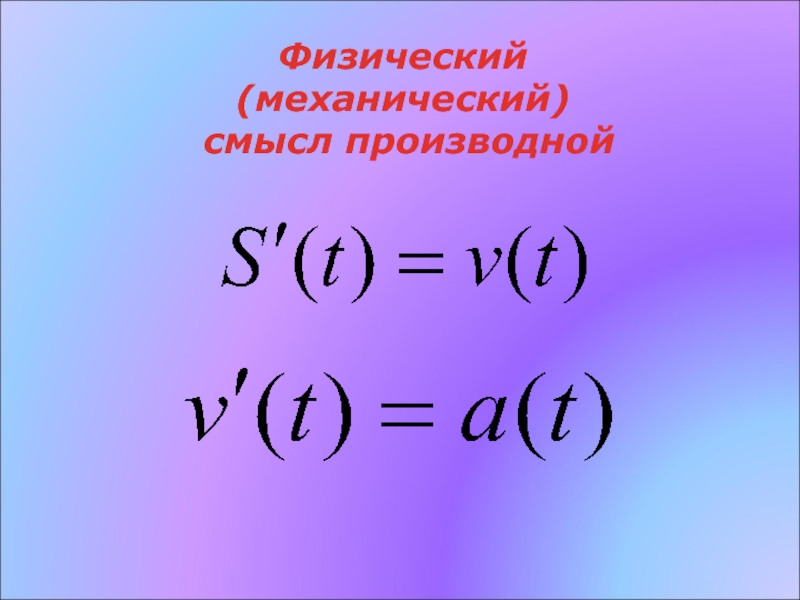- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на темы Производная 11 класс
Содержание
- 1. Презентация на темы Производная 11 класс
- 2. Таблица производных
- 3. Таблица производных
- 4. Правила дифференцирования
- 5. Найти производную функцииРешение
- 6. Решение
- 7. Решение
- 8. Решение
- 9. Решение
- 10. 6) Найдите значение производной функции в точке РешениеПерепишем заданную функцию в виде:Ответ:
- 11. Слайд 11
- 12. Слайд 12
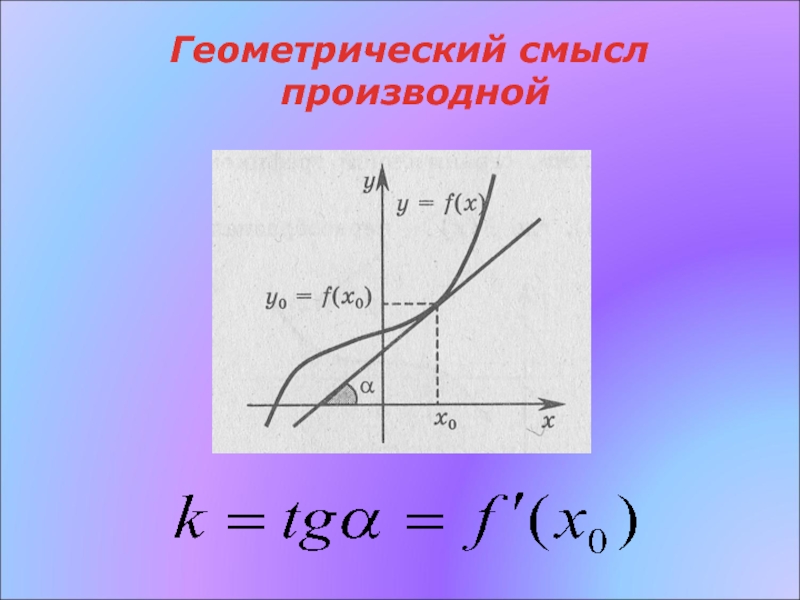
- 13. Геометрический смысл производной
- 14. Найти угловой коэффициент касательной, проведенной к графику функции в точке с абсциссойРешениеОтвет: k =2
- 15. 2) Угловой коэффициент касательной, проведенной к графику
- 16. 3) К графику функции
- 17. 4) Функции y = f(x) определена
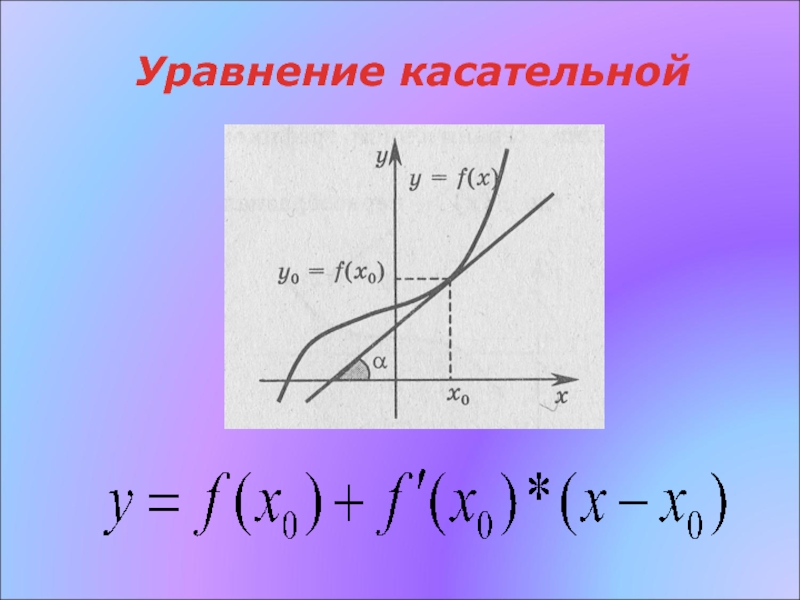
- 18. Уравнение касательной
- 19. Пример Составить уравнение касательной, проведенной
- 20. Физический (механический) смысл производной
- 21. Пример Материальная точка
- 22. Домашнее заданиеПовторить: Таблицу производных.Правила дифференцирования.3) Алгоритмы
- 23. Желаю успехов!
- 24. Информационные ресурсы:http://img.sunhome.ru/UsersGallery/Cards/155/25232105.jpg - дети
Таблица производных
Слайд 106) Найдите значение производной функции
в точке
Решение
Перепишем заданную
функцию в виде:
Ответ:
Слайд 14Найти угловой коэффициент касательной, проведенной к графику функции
в точке с
абсциссой
Решение
Ответ: k =2
Слайд 152) Угловой коэффициент касательной, проведенной к графику функции
в
точке (-2;7), равен 4. Найдите
Решение
Значит,
Ответ:
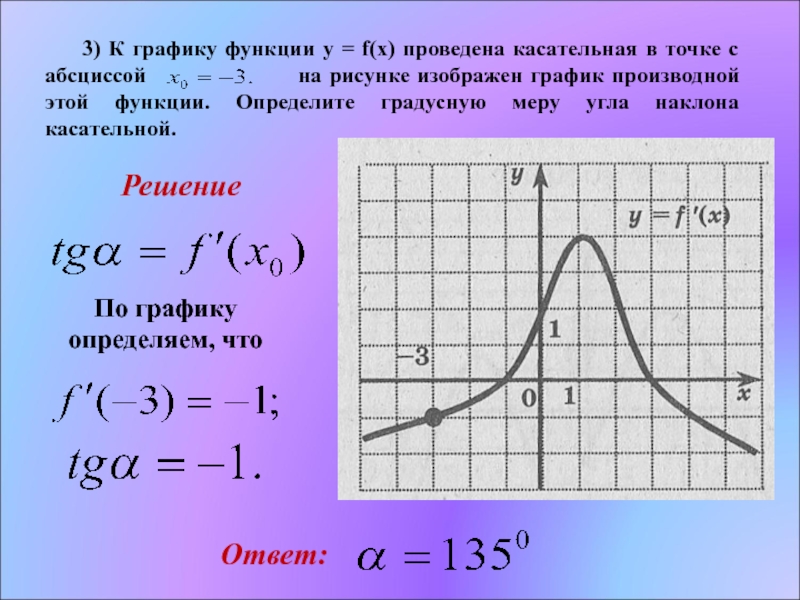
Слайд 16 3) К графику функции y = f(x) проведена
касательная в точке с абсциссой на рисунке изображен график производной этой функции. Определите градусную меру угла наклона касательной.
Решение
По графику определяем, что
Ответ:
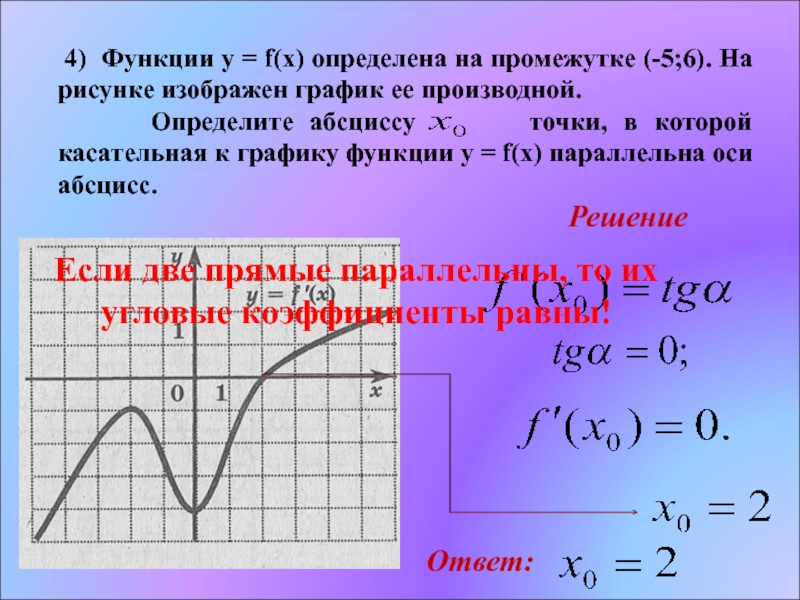
Слайд 17 4) Функции y = f(x) определена на промежутке (-5;6). На
рисунке изображен график ее производной.
Определите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна оси абсцисс.
Определите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна оси абсцисс.
Решение
Ответ:
Если две прямые параллельны, то их угловые коэффициенты равны!
Слайд 19Пример
Составить уравнение касательной, проведенной к графику функции
в точке графика с абсциссой
Решение
Ответ:
Слайд 21Пример
Материальная точка движется по прямой так,
что ее скорость в момент времени t равна
Найдите ускорение точки в момент времени t = 3.
Найдите ускорение точки в момент времени t = 3.
Решение
Ответ:
Слайд 22Домашнее задание
Повторить:
Таблицу производных.
Правила дифференцирования.
3) Алгоритмы решения ключевых задач.
Подготовить свои
вопросы
и задания по данной теме.
и задания по данной теме.