- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Методы решения тригонометрических уравнений 10 класс
Содержание
- 1. Презентация Методы решения тригонометрических уравнений 10 класс
- 2. Слайд 2
- 3. Существует 7 основных методов, с помощью которых
- 4. Теперь идем в обратном порядке cos(x +
- 5. Решение тригонометрических уравнений через разложение на множители
- 6. Получаем два уравнения Получаем два уравнения2sin(x/2) =
- 7. Делим уравнение на cos(x/2) и получаем опять
- 8. Приведение к однородному уравнению Уравнение является однородным
- 9. Пример. Решить уравнение 3sin2x
- 10. Решение уравнений, через переход к половинному углу
- 11. Заменяем tg x на y и получаем
- 12. Делим на cos(x/2): tg2 (x/2) –
- 13. Введение вспомогательного угла Для рассмотрения возьмем уравнение
- 14. Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают
- 15. Решением этого простейшего тригонометрического уравнения будет Решением
- 16. Пример. Решить уравнение sin
- 17. cos( п/6) * sin 3x – sin(
- 18. Преобразование произведения в сумму Здесь мы будем
- 19. Получаем простейшее уравнение:
- 20. Универсальная подстановка Пример. Решить тригонометрическое уравнение
- 21. 1) X (2k + 1)
- 22. Делаем замену tg(x/2) на y и
- 23. 2) x = (2k + 1)п
- 24. Основные методы решения тригонометрических уравнений, мы рассмотрели.
Слайд 3Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены
Пример.
Решить уравнение 2cos2 (x + п/6) – 3sin(п/3 – x) +1 = 0
Используя формулы приведения получим:
2cos2 (x + п/6) – 3cos(x + п/6) +1 = 0
Заменим cos(x + п/6) на y для упрощения и получаем обычное квадратное уравнение:
2y2 – 3y + 1 + 0
Корни которого y1 = 1, y2 = 1/2
Слайд 4Теперь идем в обратном порядке
cos(x + п/6) = y
Подставляем найденные значения
cos(x + п/6) = 1
x + п/6 = 2 k
x1 = - п/6 + 2 k
cos(x + п/6) =1/2
x + п/6 = ±arccos 1/2 + 2 k
x2 = ± п/3 - п/6+ 2 k
Слайд 5Решение тригонометрических уравнений через разложение на множители
Пример.
Как решить уравнение sin
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x - 2 sin2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) - 2 sin2 (x/2) = 0
2sin(x/2) * [cos(x/2) - sin(x/2)] = 0
Слайд 6Получаем два уравнения
Получаем два уравнения
2sin(x/2) = 0
Это простейшее тригонометрическое уравнение,
х/2 =п k
x1 = 2 пk
cos(x/2) - sin(x/2) = 0
Это уравнение является однородным и решается третьим методом, который мы рассмотрим ниже.
Слайд 7Делим уравнение на cos(x/2) и получаем опять же простейшее тригонометрическое уравнение:
1
tg(x/2) = 1
x/2 = arctg 1 +п k
x/2 = п/4+ пk
x2 = п/2+ 2 пk
Слайд 8Приведение к однородному уравнению
Уравнение является однородным относительно синуса и косинуса, если
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Слайд 9 Пример. Решить уравнение 3sin2x + 4 sin x • cos x
Решить уравнение 3sin2x + 4 sin x • cos x + 5 cos2x = 2
Воспользуемся формулой sin2 x + cos2 x = 1 и избавимся от открытой двойки справа:
3sin2x + 4 sin x • cos x + 5 cos x = 2sin2x + 2cos2x
sin2x + 4 sin x • cos x + 3 cos2x = 0
Делим на cos x:
tg2x + 4 tg x + 3 = 0
Слайд 10Решение уравнений, через переход к половинному углу
Пример.
Решить уравнение 3sin x
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos2 (x/2) + 5sin2 (x/2) = 7sin2 (x/2) + 7cos2 (x/2)
Переносим все влево:
2sin2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos2 (x/2) = 0
Слайд 11Заменяем tg x на y и получаем квадратное уравнение:
y2 + 4y
Отсюда находим два решения исходного уравнения:
1) tg x = –1
x1 = п/4+ пk
2) tg x = –3
x2 = arctg 3 +пk
Слайд 13Введение вспомогательного угла
Для рассмотрения возьмем уравнение вида: a sin x +
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Слайд 14Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin
cos * sin x + sin * cos x = С
или sin(x + ) = C
Слайд 15Решением этого простейшего тригонометрического уравнения будет
Решением этого простейшего тригонометрического уравнения будет
х
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Слайд 16
Пример.
Решить уравнение
sin 3x – cos 3x = 1
В этом уравнении
а = , b = -1, поэтому делим обе части
на = 2
( /2) * sin 3x – (1/2)cos 3x = 1/2
Слайд 17cos( п/6) * sin 3x – sin( п/6) * cos 3x
sin(3x – п/6) = ½
Получаем ответ
x = (-1) k * п/18 + п/18 + пk/3
Слайд 18Преобразование произведения в сумму
Здесь мы будем просто использовать тригонометрические формулы
Пример.
Решить
Левую часть преобразуем в сумму:
cos 4x – cos 8x = cos 4x
Слайд 20Универсальная подстановка
Пример.
Решить тригонометрическое уравнение
Здесь возможны 2 случая:
Слайд 211) X (2k + 1) п,
тогда, воспользовавшись тригонометрическими формулами,
3[(2tg(x/2))/(1 + tg2 (x/2)] - 4[(1 – tg2 (x/2))/(1 + tg2 (x/2)] = 3
6tg(x/2) – 4 + 4tg2 (x/2) = 3 + 3tg2 (x/2)
tg2 (x/2) + 6tg(x/2) – 7 = 0
Слайд 22 Делаем замену tg(x/2) на y и получаем квадратное уравнение: y2 + 6y
корни которого y1 = -7, y2 = 1
Идем обратно и получаем два простейших уравнения:
1) tg(x/2) = -7 2) tg(x/2) = 1
х1 = -2arctg 7 + 2п k x2 = п/2 + 2 k
Слайд 23
2) x = (2k + 1)п ,
тогда 3sin[(2k +1) п]
Получаем – решение имеет только первое условие.
















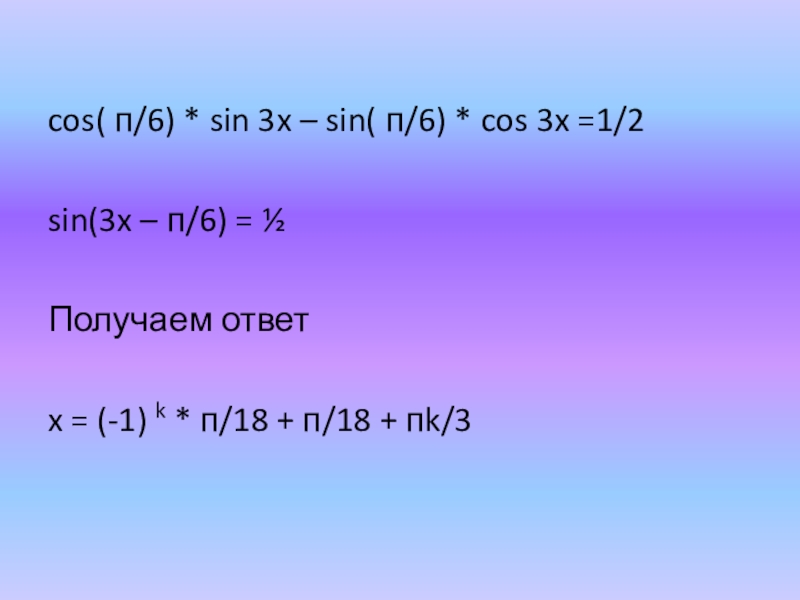



![Презентация Методы решения тригонометрических уравнений 10 класс 1) X (2k + 1) п, тогда, воспользовавшись тригонометрическими формулами, получим:3[(2tg(x/2))/(1 1) X (2k + 1) п, тогда, воспользовавшись тригонометрическими формулами, получим:3[(2tg(x/2))/(1 + tg2 (x/2)] -](/img/thumbs/745c66bfac279159fff015166db05127-800x.jpg)

![Презентация Методы решения тригонометрических уравнений 10 класс 2) x = (2k + 1)п , тогда 3sin[(2k +1) 2) x = (2k + 1)п , тогда 3sin[(2k +1) п] – 4cos[(2k + 1)п](/img/thumbs/d8d9d8d5579cd5e47a7848e1e00ede1c-800x.jpg)






