- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Теорема косинусов
Содержание
- 1. Презентация к уроку по теме Теорема косинусов
- 2. Цели урока: Доказать теорему косинусов и показать
- 3. Слайд 3
- 4. Как найти длину тоннеля, если угол С острый. Дано:
- 5. Решение: Проведем высоту АН. Из треугольника
- 6. Теорема косинусов. Квадрат стороны треугольника равен сумме
- 7. 1 способ. K
- 8. 1 способ. K
- 9. 1 способ. Если угол С прямой, тогда
- 10. 2 способ.
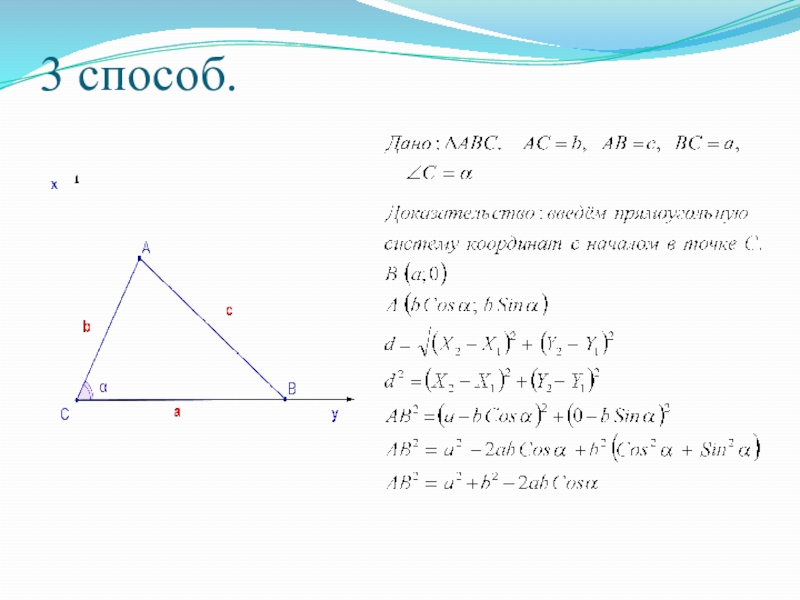
- 11. 3 способ.
- 12. Закрепление. Задача №1Определите вид ∆
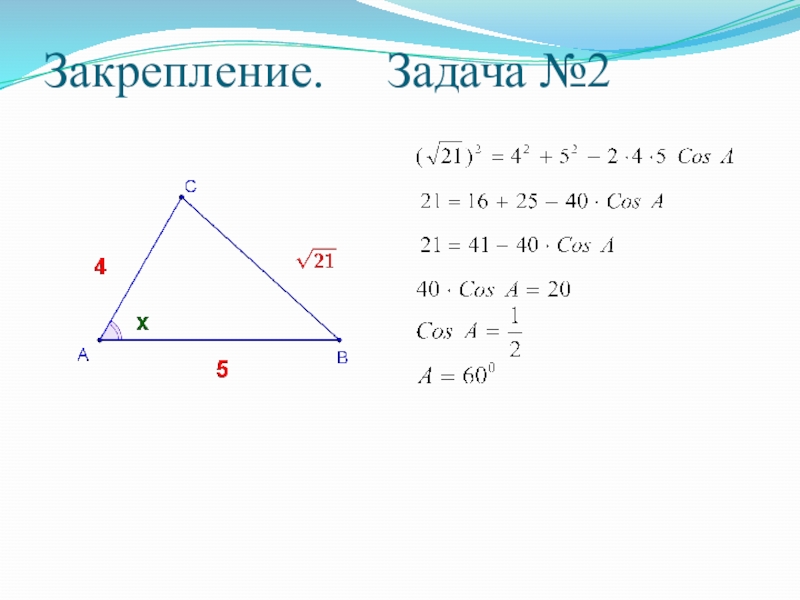
- 13. Закрепление. Задача №2
- 14. Закрепление. Задача №3
- 15. Исторический материал.
- 16. Рефлексия деятельности на уроке.1.Какой способ доказательства наиболее вам понравился и почему?2.Выучить тот способ, который наиболее доступен.
- 17. Домашнее задание:Прочитать п. 98, выполнитьУрок № 25: №1025(б, в, г). Урок № 26: №1028,1031.
- 18. Исторический материал.Начиная с древних времен и примерно
Цели урока: Доказать теорему косинусов и показать ее применение при решении задачСпособствовать усвоению обучающимися стандартного минимума по теме;Формировать и совершенствовать надпредметные умения обобщать путем сравнения, постановки и решения проблем, оперированием уже знакомыми геометрическими понятиями и фактами,
Слайд 2Цели урока:
Доказать теорему косинусов и показать ее применение при решении
задач
Способствовать усвоению обучающимися стандартного минимума по теме;
Формировать и совершенствовать надпредметные умения обобщать путем сравнения, постановки и решения проблем, оперированием уже знакомыми геометрическими понятиями и фактами, рассуждением по аналогии;
Развивать тригонометрический аппарат как средство решения геометрических задач;
Развивать психические свойства: память, вербальную и образную, произвольное внимание, воображение.
Воспитывать чувство коллективизма.
Способствовать усвоению обучающимися стандартного минимума по теме;
Формировать и совершенствовать надпредметные умения обобщать путем сравнения, постановки и решения проблем, оперированием уже знакомыми геометрическими понятиями и фактами, рассуждением по аналогии;
Развивать тригонометрический аппарат как средство решения геометрических задач;
Развивать психические свойства: память, вербальную и образную, произвольное внимание, воображение.
Воспитывать чувство коллективизма.
Слайд 3 Задача: При проектировании строительства железной
дороги на некотором участке, возникла необходимость сооружения тоннеля, сквозь выступ горы между пунктами А и В. Для
определения длины тоннеля выбрали на местности некоторый пункт С, из которого видны и доступны пункты А и В.
Чему равна длина тоннеля, если угол С равен 900.
Ответ: АВ =
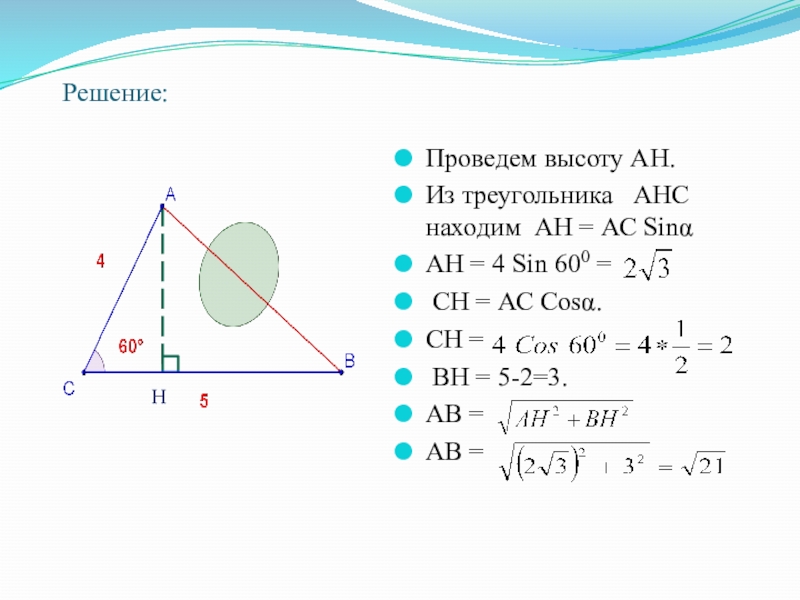
Слайд 5Решение:
Проведем высоту АН.
Из треугольника АНС находим АН = АС
Sinα
АН = 4 Sin 600 =
СН = АС Cosα.
СН =
ВН = 5-2=3.
АВ =
АВ =
АН = 4 Sin 600 =
СН = АС Cosα.
СН =
ВН = 5-2=3.
АВ =
АВ =
Н
Слайд 6Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на косинус угла между ними.
Слайд 91 способ.
Если угол С прямой,
тогда Cos C = 0 и
формула
c2 = a2 + b2 - 2ab Cos C становится в этом случае теоремой Пифагора.
Теорема косинусов является обобщенной теоремой Пифагора.
c2 = a2 + b2 - 2ab Cos C становится в этом случае теоремой Пифагора.
Теорема косинусов является обобщенной теоремой Пифагора.
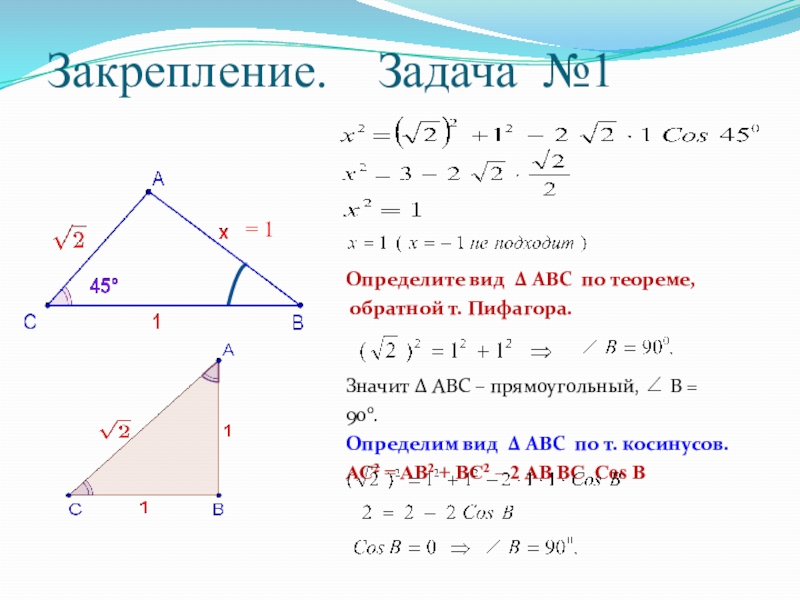
Слайд 12 Закрепление. Задача №1
Определите вид ∆ ABC по теореме,
обратной
т. Пифагора.
Значит ∆ ABC – прямоугольный, В = 900.
Определим вид ∆ ABC по т. косинусов.
АС2 = AB2 + BC2 – 2 AB BC Cos B
Значит ∆ ABC – прямоугольный, В = 900.
Определим вид ∆ ABC по т. косинусов.
АС2 = AB2 + BC2 – 2 AB BC Cos B
= 1
Слайд 16Рефлексия деятельности на уроке.
1.Какой способ доказательства наиболее вам понравился и почему?
2.Выучить
тот способ, который наиболее доступен.
Слайд 17Домашнее задание:
Прочитать п. 98, выполнить
Урок № 25: №1025(б, в, г).
Урок №
26: №1028,1031.
Слайд 18Исторический материал.
Начиная с древних времен и примерно до XVII века в
тригонометрии, рассматривали почти исключительно « решение треугольников », т.е. вычисление одних элементов треугольника по другим. Такие вычисления были вызваны запросами астрономии, географии, мореплавания, геодезии и архитектуры. Лишь в XVIII веке в содержании тригонометрии значительно расширяется.
Для решения треугольника, т.е. для нахождения трех его элементов, когда известны другие три его элемента (среди которых, по крайней мере, одна сторона), необходимо иметь три независимых соотношения между шестью его элементами. В евклидовой геометрии одно из них выражается равенством: .
В случае прямоугольного треугольника, помимо т. Пифагора, можно, например, пользоваться соотношениями .
В случае косоугольных треугольников, помимо, можно использовать т.синусов или
т. косинусов.
Теорема косинусов была по существу доказана, конечно, геометрически, еще в « Началах» Евклида, а именно в 12-м и 13-м предложениях II книги, в которой обобщается т. Пифагора и выводятся формулы, выражающие квадрат стороны, лежащей против острого или тупого угла треугольника. Это положение, доказанное Евклидом, эквивалентно теореме косинусов.
Александрийский математик Герон (I в), ученые Индии (Брахмагупта, Бхаскара), как и некоторые европейские математики XII-XV в.в. ( Л. Фибоначчи), пользовались формулами близкими к формулам т. косинусов, однако, явно была сформулирована ( словесно) в XVI в. Французским математиком Ф. Виетом.
Современный вид т. косинусов принимает в 1801 г. у французского математика Лазаря Карно (1753г- 1823г).
Для решения треугольника, т.е. для нахождения трех его элементов, когда известны другие три его элемента (среди которых, по крайней мере, одна сторона), необходимо иметь три независимых соотношения между шестью его элементами. В евклидовой геометрии одно из них выражается равенством: .
В случае прямоугольного треугольника, помимо т. Пифагора, можно, например, пользоваться соотношениями .
В случае косоугольных треугольников, помимо, можно использовать т.синусов или
т. косинусов.
Теорема косинусов была по существу доказана, конечно, геометрически, еще в « Началах» Евклида, а именно в 12-м и 13-м предложениях II книги, в которой обобщается т. Пифагора и выводятся формулы, выражающие квадрат стороны, лежащей против острого или тупого угла треугольника. Это положение, доказанное Евклидом, эквивалентно теореме косинусов.
Александрийский математик Герон (I в), ученые Индии (Брахмагупта, Бхаскара), как и некоторые европейские математики XII-XV в.в. ( Л. Фибоначчи), пользовались формулами близкими к формулам т. косинусов, однако, явно была сформулирована ( словесно) в XVI в. Французским математиком Ф. Виетом.
Современный вид т. косинусов принимает в 1801 г. у французского математика Лазаря Карно (1753г- 1823г).